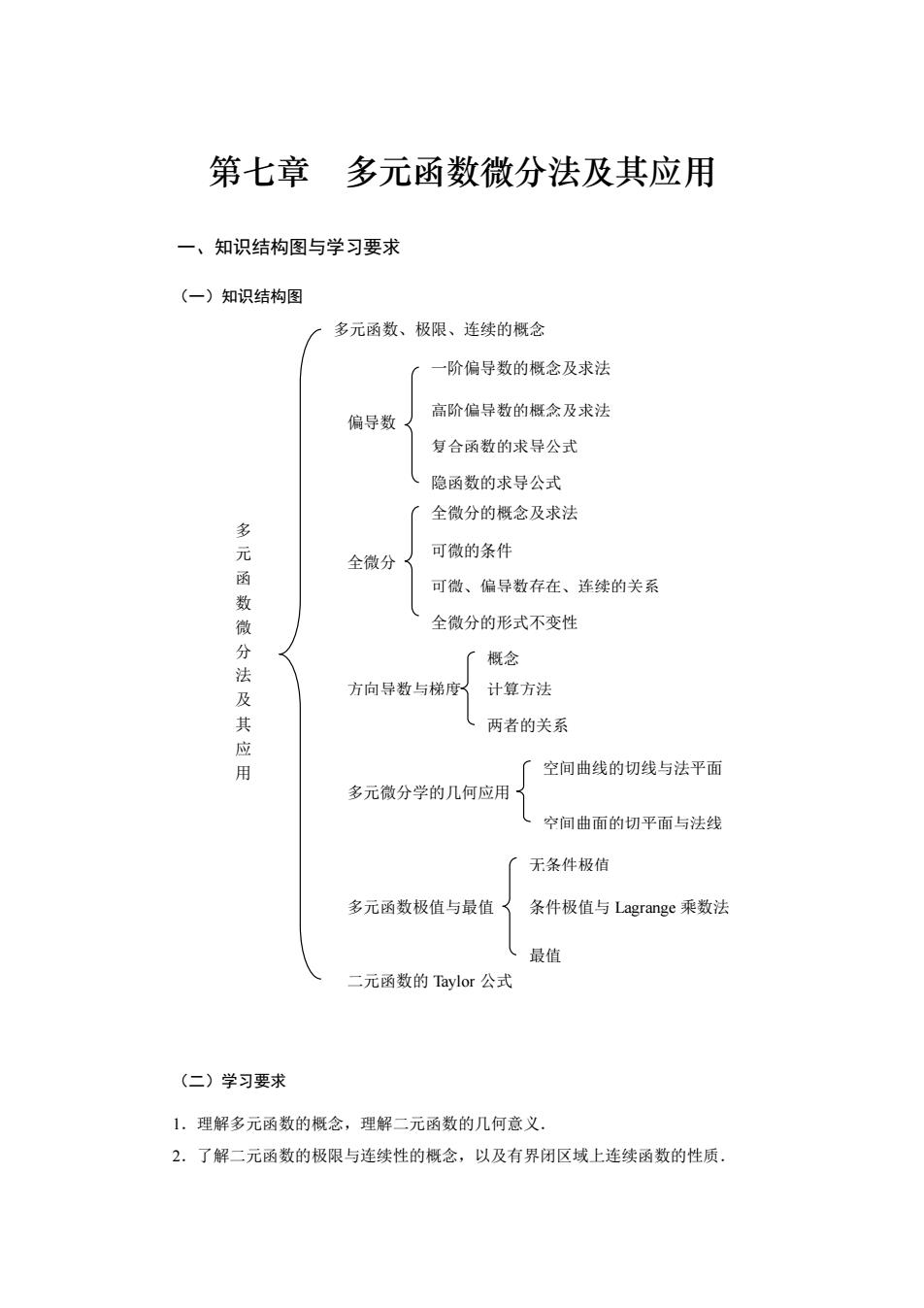
第七章多元函数微分法及其应用 一、知识结构图与学习要求 (一)知识结构图 多元函数、极限、连续的概念 -阶偏导数的概念及求法 偏导数 高阶偏导数的概念及求法 复合函数的求导公式 隐函数的求导公式 ”全微分的概念及求法 全微分 可微的条件 数 可微、偏导数存在、连续的关系 分法 全微分的形式不变性 「概念 方向导数与梯度计算方法 其应用 (两者的关系 空间曲线的切线与法平面 多元微分学的几何应用 空间曲面的切平面与法线 无条件极值 多元函数极值与最值 条件极值与Lagrange乘数法 最值 二元函数的Taylor公式 (二)学习要求 1.理解多元函数的概念,理解二元函数的几何意义. 2.了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质」
第七章 多元函数微分法及其应用 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解多元函数的概念,理解二元函数的几何意义. 2.了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质. 多 元 函 数 微 分 法 及 其 应 用 多元微分学的几何应用 空间曲线的切线与法平面 隐函数的求导公式 方向导数与梯度 一阶偏导数的概念及求法 偏导数 多元函数、极限、连续的概念 空间曲面的切平面与法线 复合函数的求导公式 概念 全微分 可微、偏导数存在、连续的关系 多元函数极值与最值 条件极值与 Lagrange 乘数法 无条件极值 全微分的概念及求法 高阶偏导数的概念及求法 可微的条件 全微分的形式不变性 二元函数的 Taylor 公式 计算方法 两者的关系 最值

3.理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和 充分条件,了解全微分形式的不变性。 4.理解方向导数与梯度的概念并掌握其计算方法 5.掌握多元复合函数一阶、二阶偏导数的求法」 6.了解隐函数存在定理,会求多元隐函数的偏导数. 7.了解空间曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程。 8.了解二元函数的二阶泰勒公式. 9.理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二 元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求 简单多元函数的最大值和最小值,并会解决一些简单的应用问题. 二、内容提要 (一)多元函数的极限与连续 1.二元函数的概念 设D是平面点集,如果对每个点P(x,y)ED,变量:按照一定的法则总有唯一确定的 值和它对应,则称:是变量x,y(或点P)的二元函数,记作:=x,)或:=fP) 称D是该函数的定义域。类似可以定义三元或三元以上的函数 2.二元函数的极限 设:=fx,)在区域D内有定义,(x%)是D的聚点,若存在常数A,使得 6>0,36>0,当P(x,y)∈DnU(P,)时, f(x,y)-A<s, 则称:=fx,)当P→B时以A为极限,记作 职在川=4或mfk以=4, 二元函数的极限也称为二重极限. 注二元函数极限的存在,等价于点P(x,)在fx,)的定义域中以任何方式趋于 B(:,%)时,x,)的极限都是A,由此可知,如果P(x,)沿某两种特殊方式趋于乃(化,) 时,f红)的极限不相同,则mx)不存在. 3.二元函数的连续性 设:=fx,)的定义域为D,B(,)为D的聚点,且B(,%)eD,如果 则称fx,)在P处连续,此时,D可以是开区域或闭区域,因此乃也可能是D的边界点.比 较一元连续函数在闭区间上的性质,二元连续函数在闭区域上也有类似的性质
3.理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和 充分条件,了解全微分形式的不变性. 4.理解方向导数与梯度的概念并掌握其计算方法. 5.掌握多元复合函数一阶、二阶偏导数的求法. 6.了解隐函数存在定理,会求多元隐函数的偏导数. 7.了解空间曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程. 8.了解二元函数的二阶泰勒公式. 9.理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二 元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求 简单多元函数的最大值和最小值,并会解决一些简单的应用问题. 二、内容提要 (一)多元函数的极限与连续 1.二元函数的概念 设 D 是平面点集,如果对每个点 P x y D ( , ) ,变量 z 按照一定的法则总有唯一确定的 值和它对应,则称 z 是变量 x , y (或点 P )的二元函数,记作 z f x y = ( , ) 或 z f P = ( ) 称 D 是该函数的定义域.类似可以定义三元或三元以上的函数. 2.二元函数的极限 设 z f x y = ( , ) 在区域 D 内有定义, 0 0 0 P x y ( , ) 是 D 的聚点,若存在常数 A ,使得 0, 0 ,当 0 P x y D U P ( , ) ( , ) 时, f x y A ( , ) − , 则称 z f x y = ( , ) 当 P P → 0 时以 A 为极限,记作 0 0 ( , ) ( , ) lim ( , ) x y x y f x y A → = 或 0 lim ( , ) P P f x y A → = , 二元函数的极限也称为二重极限. 注 二元函数极限的存在,等价于点 P x y ( , ) 在 f x y ( , ) 的定义域中以任何方式趋于 0 0 0 P x y ( , ) 时, f x y ( , ) 的极限都是 A,由此可知,如果 P x y ( , ) 沿某两种特殊方式趋于 0 0 0 P x y ( , ) 时, f x y ( , ) 的极限不相同,则 0 lim ( , ) P P f x y → 不存在. 3.二元函数的连续性 设 z f x y = ( , ) 的定义域为 D, 0 0 0 P x y ( , ) 为 D 的聚点,且 0 0 0 P x y D ( , ) ,如果 0 0 0 0 ( , ) ( , ) lim ( , ) ( , ) x y x y f x y f x y → = , 则称 f x y ( , ) 在 P0 处连续.此时,D 可以是开区域或闭区域,因此 P0 也可能是 D 的边界点.比 较一元连续函数在闭区间上的性质,二元连续函数在闭区域上也有类似的性质.

(二)偏导数与全微分 1.偏导数定义 如果 码+A-2 存在,则称此极限为函数:=fx,)在点乃(x,)处关于x的偏导数,记为 或鼠 6=画+4-f △y 为:=x,)在(x,为)处关于y的偏导数.在不引起混淆的情况下,有时为了记号的简单, 也将%)和f()记为x)和6). 由偏导数的定义可知,求偏导数实质上是求一元函数的导数的问题,如 0-孟 因此,一元函数的求导公式和求导法则对求偏导数也是适用的, 对三元或三元以上的多元函数亦可定义相应的偏导数. 2.偏导数几何意义 二元函数:=了化)在点(化,)的偏导数,)表示空间曲线r:任”在点 y=% M(不,fx乃》处的切线对x轴的斜率。 3.高阶偏导数 设话数:=化)在区城D内其有偶号数会小,年=,那么在D内 (x,(x,)都是(x,)的函数.如果这两个函数的偏导数也存在,则称它们为函数 :=(x,y)的二阶偏导数.按照对变量求导次序的不同有下列四个二阶偏导数 )-等-cm (器-: )点= 其中后边两个偏导数称为混合偏导数. 4.二阶混合偏导数相等的充分条件 如果函数的两个二阶混合偏号数需及器在区城口内莲续,影么在该区该内这两个
(二)偏导数与全微分 1.偏导数定义 如果 0 0 0 0 0 ( , ) ( , ) lim x f x x y f x y → x + − 存在,则称此极限为函数 z f x y = ( , ) 在点 0 0 0 P x y ( , ) 处关于 x 的偏导数,记为 0 0 0 0 ( , ), x P P f z f x y x x 或 . 称 0 0 0 0 0 0 0 ( , ) ( , ) y ( , ) lim y f x y y f x y f x y → y + − = 为 z f x y = ( , ) 在 0 0 0 P x y ( , ) 处关于 y 的偏导数.在不引起混淆的情况下,有时为了记号的简单, 也将 0 0 ( , ) x f x y 和 0 0 ( , ) y f x y 记为 1 0 0 f x y ( , ) 和 2 0 0 f x y ( , ) . 由偏导数的定义可知,求偏导数实质上是求一元函数的导数的问题,如 0 0 0 0 ( , ) ( , ) x x x d f x y f x y dx = = . 因此,一元函数的求导公式和求导法则对求偏导数也是适用的. 对三元或三元以上的多元函数亦可定义相应的偏导数. 2.偏导数几何意义 二元函数 z f x y = ( , ) 在点 0 0 ( , ) x y 的偏导数 0 0 ( , ) x f x y 表示空间曲线 0 ( , ) : z f x y y y = = 在点 0 0 0 0 M x y f x y ( , , ( , )) 处的切线对 x 轴的斜率. 3.高阶偏导数 设函数 z f x y = ( , ) 在区域 D 内具有偏导数 ( , ) x z f x y x = , ( , ) y z f x y y = ,那么在 D 内 ( , ) x f x y , ( , ) y f x y 都是 ( , ) x y 的函数.如果这两个函数的偏导数也存在,则称它们为函数 z f x y = ( , ) 的二阶偏导数.按照对变量求导次序的不同有下列四个二阶偏导数 2 2 ( , ) xx z z f x y x x x = = , 2 2 ( , ) yy z z f x y y y y = = , 2 ( , ) xy z z f x y y x x y = = , 2 ( , ) yx z z f x y x y y x = = , 其中后边两个偏导数称为混合偏导数. 4.二阶混合偏导数相等的充分条件 如果函数的两个二阶混合偏导数 2 z x y 及 2 z y x 在区域 D 内连续,那么在该区域内这两个

三价混合滨号数必相等,即需 5.全微分的定义 设:=f(xy)在区域D内有定义,(x,)∈eD,(x+△x,y+A)eD,若存在与△x,△y无 关的A和B,使 A=f(x+A.y+Ay)-f(x.y)=MAx+BAy+ap),p=y0. 则称∫x,)在(x,)处可微,且称止=AAx+BAy为∫x,)在(x,)处的全微分. 二元函数的可微性是一元函数的可微性的推广.若:=(x,y)在(x,y)处可微,则它在 (x)处连续。一元函数可微与可导等价,但二元函数可微和存在偏导数却没有这样的关 系。实际上,若fx)在(x,)处可微,则它在该点处的偏导数存在,且全微分为 但反之则不一定成立,比如本章例14. 6.判别函数可微通常有两种方法 方法1若:=fxy)在(x,)的某邻域中的偏导数f(x,y)和(x,y)存在,且f(x,y) 和(x,)在(x,)处连续,则fx)在(x,)处可微. 方法2首先求x,)和(x),如果 -+0. 其中 L=fx+△xy+A)-fx,),p=V△r2+Ay2, 则fx,)在(x,)处可微 在利用方法1来确定∫x,)的可微性时,通常根据多元初等函数的连续性可知x,) 有连续的偏导数.而适用于方法2的具体问题往往是考虑x,)在一些特殊点的可微性。 其中(x,y)和∫x,y)一般要用定义求得. (三)多元复合函数微分法 1.复合函数的一阶偏导数 设:=fu,)可微,u=x,y)和v=x,)存在偏导数,则:=几x,以,x,叨有如下 关于x和y的偏导数: =+Ya色_Yu+ 特别地,若u=x),v=x),则:=几x(x刃对x的导数为 会杂+安
二阶混合偏导数必相等,即 2 z x y = 2 z y x . 5.全微分的定义 设 z f x y = ( , ) 在区域 D 内有定义, ( , ) , ( , ) x y D x x y y D + + ,若存在与 x ,y 无 关的 A 和 B,使 = + + − = + + z f x y y f x y A x B y o ( , ) ( , ) ( ) , 2 2 = + → x y 0 , 则称 f x y ( , ) 在 ( , ) x y 处可微,且称 dz A x B y = + 为 f x y ( , ) 在 ( , ) x y 处的全微分. 二元函数的可微性是一元函数的可微性的推广.若 z f x y = ( , ) 在 ( , ) x y 处可微,则它在 ( , ) x y 处连续.一元函数可微与可导等价,但二元函数可微和存在偏导数却没有这样的关 系.实际上,若 f x y ( , ) 在 ( , ) x y 处可微,则它在该点处的偏导数存在,且全微分为 z z dz dx dy x y = + . 但反之则不一定成立,比如本章例 14. 6.判别函数可微通常有两种方法 方法 1 若 z f x y = ( , ) 在 ( , ) x y 的某邻域中的偏导数 ( , ) x f x y 和 ( , ) y f x y 存在,且 ( , ) x f x y 和 ( , ) y f x y 在 ( , ) x y 处连续,则 f x y ( , ) 在 ( , ) x y 处可微. 方法 2 首先求 ( , ) x f x y 和 ( , ) y f x y ,如果 0 [ ( , ) ( , ) ] lim 0 x y z f x y x f x y y → − + = , 其中 = + + − z f x x y y f x y ( , ) ( , ) , 2 2 = + x y , 则 f x y ( , ) 在 ( , ) x y 处可微. 在利用方法 1 来确定 f x y ( , ) 的可微性时,通常根据多元初等函数的连续性可知 f x y ( , ) 有连续的偏导数.而适用于方法 2 的具体问题往往是考虑 f x y ( , ) 在一些特殊点的可微性, 其中 ( , ) x f x y 和 ( , ) y f x y 一般要用定义求得. (三)多元复合函数微分法 1.复合函数的一阶偏导数 设 z f u v = ( , ) 可微, u u x y = ( , ) 和 v v x y = ( , ) 存在偏导数,则 z f u x y v x y = [ ( , ), ( , )] 有如下 关于 x 和 y 的偏导数: , z f u f v z f u f v x u x v x y u y v y = + = + . 特别地,若 u u x = ( ), v v x = ( ) ,则 z f u x v x = [ ( ), ( )] 对 x 的导数为 dz f du f dv dx u dx v dx = + .

称上述求导(或偏导)的公式为链式法则. 注这里要注意求偏导数的对象,即是对复合前的函数求导数(或偏导数),还是对复 合后的函数求偏导,例如 这里的表示复合前的二元函数:=化)关于x求偏导数,面失则表示复合以后的函数 =f化,(x》关于x求导数,二者切不可混为一谈. 2.一阶微分形式的不变性 设:=f(u,),u=x,y以,v=(x,)均可微,则无论将:=fu,)视为u、v的函数, 或视为x、y的函数,其微分相同,称之为一阶微分形式的不变性.该性质可用来求多元复 合函数的偏导数,而无需关注变量之间的关系, (四)隐函数的微分法 1.一个方程确定的隐函数 隐函数存在定理1设Fx,)在点P(x,%)的某一邻域内具有连续偏导数,且 Fx,)=0,F6)≠0,则方程F(x,)=0在点(化,)的某一邻域内恒能唯一确定 个连续且具有连续导数的函数y=x),它满足条件=(x),并有 dy F(x.) 若F(x,)有二阶连续偏导,则在相应条件下,有 0-2 隐函数存在定理2设函数F(x,y)点P(x,)的某一邻域内具有连续偏导数,且 F(x,)=0,F'(x,%,o)≠0,则方程F(x,y,)=0在点(30,)的某一邻域内恒能唯 一确定一个连续且具有连续偏导数的函数:=(x,),它满足条件。=x,),并有 正F(x aFx,y,) axE(x.v.)' ayF(x.y.=)' 2.方程组确定的隐函数 设方程组业丝二0确定隐函数“=(x以=x),记 J-0EGIF a可GGo, 则对方程组关于x和y求偏导数可得
称上述求导(或偏导)的公式为链式法则. 注 这里要注意求偏导数的对象,即是对复合前的函数求导数(或偏导数),还是对复 合后的函数求偏导,例如 z f x y x = ( , ( )) , dz f f dy dx x y dx = + , 这里的 f x 表示复合前的二元函数 z f x y = ( , ) 关于 x 求偏导数,而 dz dx 则表示复合以后的函数 z f x y x = ( , ( )) 关于 x 求导数,二者切不可混为一谈. 2.一阶微分形式的不变性 设 z f u v = ( , ),u u x y v v x y = = ( , ), ( , ) 均可微,则无论将 z f u v = ( , ) 视为 u 、v 的函数, 或视为 x 、y 的函数,其微分相同,称之为一阶微分形式的不变性.该性质可用来求多元复 合函数的偏导数,而无需关注变量之间的关系. (四)隐函数的微分法 1.一个方程确定的隐函数 隐函数存在定理 1 设 F x y ( , ) 在点 0 0 P x y ( , ) 的某一邻域内具有连续偏导数,且 0 0 F x y ( , ) 0 = , 0 0 ( , ) 0 F x y y ,则方程 F x y ( , ) 0 = 在点 0 0 ( , ) x y 的某一邻域内恒能唯一确定一 个连续且具有连续导数的函数 y y x = ( ) ,它满足条件 0 0 y f x = ( ) ,并有 ( , ) ( , ) x y dy F x y dx F x y = − . 若 F x y ( , ) 有二阶连续偏导,则在相应条件下,有 2 2 2 2 3 2 xx y xy x y yy x y d y F F F F F F F dx F − + = − . 隐函数存在定理 2 设函数 F x y z ( , , ) 点 0 0 0 P x y z ( , , ) 的某一邻域内具有连续偏导数,且 0 0 0 F x y z ( , , ) 0 = , 0 0 0 ( , , ) 0 F x y z z ,则方程 F x y z ( , , ) 0 = 在点 0 0 0 ( , , ) x y z 的某一邻域内恒能唯 一确定一个连续且具有连续偏导数的函数 z z x y = ( , ) ,它满足条件 0 0 0 z f x y = ( , ) ,并有 ( , , ) ( , , ) , ( , , ) ( , , ) x y z z z z F x y z F x y z x F x y z y F x y z = − = − . 2.方程组确定的隐函数 设方程组 ( , , , ) 0 ( , , , ) 0 F x y u v G x y u v = = 确定隐函数 u u x y v v x y = = ( , ), ( , ) ,记 ( , ) 0 ( , ) u v u v F G F F J u v G G = = , 则对方程组关于 x 和 y 求偏导数可得

会9会9 Ja(y,v) 特别地,若方程组二以确定的隐函数(即反函数)为u=化以P=》,则 du=1 dx dy 1 dox dy Jov Jm 种-20.由可验01 这里并不是要求读者记忆这些公式,而是要掌握推导它们的方法,即由方程组两边对自 变量求偏导数的方法· (五)方向导数与梯度 1.方向导数 (I)设:=fx)在P)的某个邻域内有定义,方向向量1={cos,cos,若极 g+posah+pos)-f,2 0 存在,则称该极限为通数门在点月处酒1方向的方向号数。记为乱 (2)设:=fx,)在(x)处可微,则fx)在P处沿任何方向1={cosa,c0sB的 方向导数都存在,且乳 =f(xYo)cosa+f(x)cosB. (3)偏导数给出了函数沿坐标轴方向的变化率,而方向导数则可刻画函数沿不同方向 的变化率,因此其在实际问愿中有重要的应用。 (4)对三元函数u=x,y,)类似地亦可定义相应的方向导数。 2.梯度 设二元高数:=刀在点化列存在一价连续偏号数,则称向最n了一甚}为 ∫x,)在点(x,)的梯度.同样地,对可求偏导的三元函数u=∫x,y,),其梯度为 ndr-甚哥
1 ( , ) ( , ) u F G x J x v = − , 1 ( , ) ( , ) v F G x J u x = − , 1 ( , ) ( , ) u F G y J y v = − , 1 ( , ) ( , ) v F G y J u y = − . 特别地,若方程组 ( , ) ( , ) x x u v y y u v = = 确定的隐函数(即反函数)为 u u x y v v x y = = ( , ), ( , ) ,则 u y 1 x J v = , v y 1 x J u = − , u x 1 y J v = − , v x 1 y J u = , 其中 ( , ) 0 ( , ) x y J u v = .由此可验证 ( , ) ( , ) 1 ( , ) ( , ) x y u v u v x y = . 这里并不是要求读者记忆这些公式,而是要掌握推导它们的方法,即由方程组两边对自 变量求偏导数的方法 . (五)方向导数与梯度 1.方向导数 (1)设 z f x y = ( , ) 在 0 0 0 P x y ( , ) 的某个邻域内有定义,方向向量 l ={cos ,cos } ,若极 限 0 0 0 0 0 ( cos , cos ) ( , ) lim f x y f x y → + + + − 存在,则称该极限为函数 f x y ( , ) 在点 P0 处沿 l 方向的方向导数,记为 P0 f l . (2)设 z f x y = ( , ) 在 0 0 0 P x y ( , ) 处可微,则 f x y ( , ) 在 P0 处沿任何方向 l ={cos ,cos } 的 方向导数都存在,且 0 0 0 0 0 ( , )cos ( , )cos x y P f f x y f x y l = + . (3)偏导数给出了函数沿坐标轴方向的变化率,而方向导数则可刻画函数沿不同方向 的变化率,因此其在实际问题中有重要的应用. (4)对三元函数 u f x y z = ( , , ) 类似地亦可定义相应的方向导数. 2.梯度 设二元函数 z f x y = ( , ) 在点 ( , ) x y 存在一阶连续偏导数,则称向量 , f f f = x y grad 为 f x y ( , ) 在点 ( , ) x y 的梯度.同样地,对可求偏导的三元函数 u f x y z = ( , , ) ,其梯度为 , , fff f = x y z grad .

3.方向导数和梯度的关系 若u=fx,y=)在(x,y,)处可微,则其沿1={cosa,c0sB,cosy方向的方向导数可表示 成=gdm1由此可知,“=化)在(K八)处沿梯度方向的方向导数最大,且方向 导数的最大值为梯度的模,即 md图g图 (六)二元函数可微、偏导数、方向导数、连续、极限各概念之间的关系 一阶偏导连续、三全微分存在日 】连续、极限存在 方向导数存在 偏导数存在 其中符号“一”表示可以推出,“十一”表示不能推出 (七)偏导数在几何上的应用 1.空间曲线的切线与法平面 (1)设Γ为光滑的空间曲线,其参数方程为「:x=x),y=),:=0.它在1=,对 应的点(伍,)=(x,化,》处的切线方程为 -1y-1-m L x6)y46)) 其相应的法平面方程为 π:x'《()x-x)+y《)-)+'(t(三-)=0 x=x (2)特别地,若Γ的方程为r= =(x ,将其视为参数方程r:{y=以x),因此,『在 (x,6)=(x,(x人(x》处的切线方程为
3.方向导数和梯度的关系 若 u f x y z = ( , , ) 在 ( , , ) x y z 处可微,则其沿 l ={cos ,cos ,cos } 方向的方向导数可表示 成 u u l = grad l 由此可知, u f x y z = ( , , ) 在 ( , , ) x y z 处沿梯度方向的方向导数最大,且方向 导数的最大值为梯度的模,即 2 2 2 fff u x y z = + + grad . (六)二元函数可微、偏导数、方向导数、连续、极限各概念之间的关系 其中符号“ ” 表示可以推出,“ ”表示不能推出. (七)偏导数在几何上的应用 1.空间曲线的切线与法平面 (1)设 为光滑的空间曲线,其参数方程为 = = = : ( ), ( ), ( ) x x t y y t z z t .它在 0 t t = 对 应的点 0 0 0 0 0 0 ( , , ) ( ( ), ( ), ( )) x y z x t y t z t = 处的切线方程为 0 0 0 0 0 0 : ( ) ( ) ( ) x x y y z z L x t y t z t − − − = = , 其相应的法平面方程为 0 0 0 0 0 0 : ( )( ) ( )( ) ( )( ) 0 x t x x y t y y z t z z − + − + − = . (2)特别地,若 的方程为 ( ) : ( ) y y x z z x = = ,将其视为参数方程 : ( ) ( ) x x y y x z z x = = = ,因此, 在 0 0 0 0 0 0 ( , , ) ( , ( ), ( )) x y z x y x z x = 处的切线方程为 0 0 0 0 0 1 ( ) ( ) x x y y z z y x z x − − − = = . 一阶偏导连续 全微分存在 连续 极限存在 方向导数存在 偏导数存在

(G》设空自线r的方程是以(C对8的影式给出质r在点人 处的切线方程为 曲线厂在点M。(,0,)处的法平面方程为 G,G.N. 2.曲面的切平面和法线 设光滑曲面S的方程为S:F(xy)=0,则S在M。(,)处的切平面方程为 F(Mx-x)+F(M0-%)+F(M:-)=0, 相应的法线方程为 特别地,若S的方程为:=∫x,y),则相应的切平面和法线方程分别为 x-x)+60-%)-(-o)=0 导 X一 其中6=f) (八)多元函数的极值 1.二元函数的一般极值 (1)设点B(,%)是二元函数:=f)定义域中的一个内点,若存在6>0,使得当 Px,)e(B,6)时,有fx)<fx,),则称fx)在点B处取得极大值,fx,)称 为x,)的极大值,P称为(x,)的极大值点。类似地可以定义极小值以及极小值点。 (2)若:=fx,)在点乃(化,)处的偏导数存在,且x,6)=x,)=0,则称卫 为fx,)的驻点(或稳定点). 若函数:=fx,)在点乃(3儿)处的偏导数存在且取得极值,则R一定为x,)的驻 点,因此,若:=fx,y)在区域D内偏导数存在,则xy)在D内的极值点一定是驻点
(3)设空间曲线 的方程是以 ( , , ) 0 ( , , ) 0 F x y z G x y z = = 的形式给出, 则曲线 在点 0 0 0 0 M x y z ( , , ) 处的切线方程为 0 0 0 0 0 0 y z z x x y y z x y M M z x M x x y y z z F F F F F F G G G G G G − − − = = . 曲线 在点 0 0 0 0 M x y z ( , , ) 处的法平面方程为 0 0 0 0 0 0 ( ) ( ) ( ) 0 y z x y z x y z z x x y M M M F F F F F F x x y y z z G G G G G G − + − + − = . 2.曲面的切平面和法线 设光滑曲面 S 的方程为 S F x y z : ( , , ) 0 = ,则 S 在 0 0 0 0 M x y z ( , , ) 处的切平面方程为 0 0 0 0 0 0 ( )( ) ( )( ) ( )( ) 0 F M x x F M y y F M z z x y z − + − + − = , 相应的法线方程为 0 0 0 0 0 0 ( ) ( ) ( ) x y z x x y y z z F M F M F M − − − = = . 特别地,若 S 的方程为 z f x y = ( , ), 则相应的切平面和法线方程分别为 0 0 0 0 0 0 0 ( , )( ) ( , )( ) ( ) 0 x y f x y x x f x y y y z z − + − − − = 和 0 0 0 0 0 0 0 ( , ) ( , ) 1 x y x x y x z z f x y f x y − − − = = − , 其中 0 0 0 z f x y = ( , ) . (八)多元函数的极值 1.二元函数的一般极值 (1)设点 0 0 0 P x y ( , ) 是二元函数 z f x y = ( , ) 定义域中的一个内点,若存在 0 ,使得当 0 P x y U P ( , ) ( , ) 时,有 0 0 f x y f x y ( , ) ( , ) ,则称 f x y ( , ) 在点 P0 处取得极大值, 0 0 f x y ( , ) 称 为 f x y ( , ) 的极大值, P0 称为 f x y ( , ) 的极大值点. 类似地可以定义极小值以及极小值点. (2)若 z f x y = ( , ) 在点 0 0 0 P x y ( , ) 处的偏导数存在,且 0 0 0 0 ( , ) ( , ) 0 x y f x y f x y = = ,则称 P0 为 f x y ( , ) 的驻点(或稳定点). 若函数 z f x y = ( , ) 在点 0 0 0 P x y ( , ) 处的偏导数存在且取得极值,则 P0 一定为 f x y ( , ) 的驻 点,因此,若 z f x y = ( , ) 在区域 D 内偏导数存在,则 f x y ( , ) 在 D 内的极值点一定是驻点.

(3)二元函数取得极值的必要条件:设函数:=fx,y)在点B(:,)具有偏导数,且 在点(化)处有极值,则有x)=36)=0. (4)二元函数取得极值的充分条件:设:=,)在P(:,)处存在二阶连续偏导数, )为fx)的驻点,记 A=),B=(o-),C=() 则有 4>0 A=AC-B2 A>0 4<0 4=0 A<0 fx)在(化)处 取极小值 取极大值 不取极值 是否取极值不能确 定,需另作讨论 2.条件极值 求函数fx,)在条件x,)=0下的极值的方法与步骤 (1)令F(x52)=fx)+0x,): (2)求使正=正==0的点(),即为可能的极值点 (3)由函数取得极值的充分条件或定义来确定(,)是否为极值点: (4)求极值. 上述方法称为拉格朗日乘数法,该方法可推广到多个变量的函数在多个约束条件下的条 件极值问题.例如,要求函数u=fxy,:,)在附加条件(x,八,:,)=0和y(化,y,)=0 下的极值: 可以先作拉格朗日函数Lx=,)=x,y,)+x,水,)+4x=,)其中元“均 为参数,求其一阶偏导数,并令一阶偏导数为零,然后与两个附加条件方程联立起来求解, 这样得出的(化,o,)就是函数u=fx以,)在附加条件o(x,以,)=0和w(x以,)=0 下的可能极值点.再由函数取得极值的充分条件或定义来确定(化,)是否为极值点。 3.最值 若fx,)在有界闭区域D上连续,则fx,)在D上存在最大值和最小值,求最大值利 最小值的方法是:求出x,)在D内的驻点和偏导数不存在的点,将其函数值与∫x,)在 D的边界上的最大值和最小值进行比较,最大者为最大值,而最小者为最小值。 (九)二元函数的泰勒公式 设:=f(x)在点(化,为)的某一邻域内连续且有直到n+1阶的连续偏导数, (伍。+h,%+)为此邻域内任一点,则有
(3)二元函数取得极值的必要条件:设函数 z f x y = ( , ) 在点 0 0 0 P x y ( , ) 具有偏导数,且 在点 0 0 0 P x y ( , ) 处有极值,则有 0 0 0 0 ( , ) ( , ) 0 x y f x y f x y = = . (4)二元函数取得极值的充分条件:设 z f x y = ( , ) 在 0 0 0 P x y ( , ) 处存在二阶连续偏导数, 0 0 0 P x y ( , ) 为 f x y ( , ) 的驻点,记 0 0 ( , ) A f x y xx = , 0 0 ( , ) B f x y xy = , 0 0 ( , ) C f x y yy = , 则有 2 = − AC B 0 0 = 0 A>0 A<0 f x y ( , ) 在 0 0 ( , ) x y 处 取极小值 取极大值 不取极值 是否取极值不能确 定,需另作讨论 2.条件极值 求函数 f x y ( , ) 在条件 ( , ) 0 x y = 下的极值的方法与步骤: (1)令 F x y f x y x y ( , , ) ( , ) ( , ) = + ; (2)求使 0 FFF x y === 的点 0 0 ( , ) x y ,即为可能的极值点; (3)由函数取得极值的充分条件或定义来确定 0 0 ( , ) x y 是否为极值点; (4)求极值. 上述方法称为拉格朗日乘数法.该方法可推广到多个变量的函数在多个约束条件下的条 件极值问题.例如,要求函数 u f x y z t = ( , , , ) 在附加条件 ( , , , ) 0 x y z t = 和 ( , , , ) 0 x y z t = 下的极值: 可以先作拉格朗日函数 L x y z t f x y z t x y z t x y z t ( , , , ) ( , , , ) ( , , , ) ( , , , ), = + + 其中 , 均 为参数,求其一阶偏导数,并令一阶偏导数为零,然后与两个附加条件方程联立起来求解, 这样得出的 0 0 0 0 ( , , , ) x y z t 就是函数 u f x y z t = ( , , , ) 在附加条件 ( , , , ) 0 x y z t = 和 ( , , , ) 0 x y z t = 下的可能极值点.再由函数取得极值的充分条件或定义来确定 0 0 0 0 ( , , , ) x y z t 是否为极值点. 3.最值 若 f x y ( , ) 在有界闭区域 D 上连续,则 f x y ( , ) 在 D 上存在最大值和最小值,求最大值和 最小值的方法是:求出 f x y ( , ) 在 D 内的驻点和偏导数不存在的点,将其函数值与 f x y ( , ) 在 D 的边界上的最大值和最小值进行比较,最大者为最大值,而最小者为最小值. (九)二元函数的泰勒公式 设 z f x y = ( , ) 在点 0 0 ( , ) x y 的某 一邻 域内 连续 且有直 到 n +1 阶的连 续偏 导数, 0 0 ( , ) x h y k + + 为此邻域内任一点,则有 2 0 0 0 0 0 0 0 0 1 ( , ) ( , ) ( , ) ( , ) 2! f x h y k f x y h k f x y h k f x y x y x y + + = + + + +

(0<0<,其中记号 (会号}6)表示60+x小 (侵+号化)表示化+2化+化 般地,记号 g+标ggwa
1 0 0 0 0 1 1 ( , ) ( , ) ! ( 1)! n n h k f x y h k f x h y k n x y n x y + + + + + + + + + , (0 1) ,其中记号 0 0 h k f x y ( , ) x y + 表示 0 0 0 0 ( , ) ( , ), x y hf x y kf x y + 2 0 0 h k f x y ( , ) x y + 表示 2 2 0 0 0 0 0 0 ( , ) 2 ( , ) ( , ), xx xy yy h f x y hkf x y k f x y + + 一般地,记号 0 0 ( , ) m h k f x y x y + 表示 0 0 0 ( , ) m m p p m p m p m p p x y f C h k x y − − = .