
第六章 空间解析几何 数学实验 Mat1ab软件为我们提供了众多的功能强大的绘制空间图形的函数,它们分别是plot3, mesh,meshc,meshz,meshgrid,sphere,cylinder,hesurfc等等,下面分别介绍. “、空间曲线的绘制 plot3是Matlab中最常用的画空间曲线的函数,它的主要功能是用于绘制显示函数 =,)和参数式函数x=0,y=0, :=的空间曲线,也可以用空间中的一组平 行平面上的截线的方式表示曲面.plot3函数的调用格式与lot十分相似,具体如下: plot3(x.y.z. 可选项s') 其中如果x,y,:为同维数的向量时,则绘制以x,y,:元素为横、纵、竖坐标的三维曲 线:如果x,y,z为同维矩阵时,则以x,y,z对应元素为横、纵、竖坐标分别绘制曲线, 曲线条数等于矩阵的列数.曲线上的'可选项s'中通常包含确定曲线颜色、线型、两坐标轴 上的比例等等的参数.用户在作图时可以根据需要选择可选项,如果不用可选项,那么pl0t3 函数将自动选择一组默认值,画出空间曲线。 例1作出以方程x=6”c0s受,y=c”sm1,=1,10,2刘表示的空间曲线。 解相应的Matlab程序为 >t=0:0.01:20: >x=exp(-0.2*t).*cos(0.5*pi*t):y=exp(-0.2*t).*sin(0.5*和i*t):z=t: >>plot3(x,y,z): >text(x(1),y(1),z(1),'start'); %在(x(1),y(1),z(1)处加标字符串 'start' >n=length(x):text(x(n,y(m),z(n),'end');%在(x(n),y(n,z(m)处加标字符串 'end' >xlabel(CX'):ylabel('Y'),zlabel(CZ');%说明坐标轴标记 >grid on: %grid on/,grid off为显示/不显示格栅命令 运行结果如图6-47
1 第六章 空间解析几何 数学实验 Matlab 软件为我们提供了众多的功能强大的绘制空间图形的函数,它们分别是 plot3, mesh,meshc,meshz,meshgrid,sphere,cylinder,hesurfc 等等,下面分别介绍. 一、空间曲线的绘制 plot3 是 Matlab 中最常用的画空间曲线的函数,它的主要功能是用于绘制显示函数 z f x y = ( , ) 和参数式函数 x x t = ( ) , y y t = ( ) , z z t = ( ) 的空间曲线,也可以用空间中的一组平 行平面上的截线的方式表示曲面. plot3 函数的调用格式与 plot 十分相似,具体如下: plot3(x,y,z, ′可选项 s′) 其中如果 x , y , z 为同维数的向量时,则绘制以 x , y ,z 元素为横、纵、竖坐标的三维曲 线;如果 x,y,z 为同维矩阵时,则以 x,y,z 对应元素为横、纵、竖坐标分别绘制曲线, 曲线条数等于矩阵的列数.曲线上的′可选项 s′中通常包含确定曲线颜色、线型、两坐标轴 上的比例等等的参数.用户在作图时可以根据需要选择可选项,如果不用可选项,那么 plot3 函数将自动选择一组默认值,画出空间曲线. 例 1 作出以方程 0.2 e cos 2 t x t − = , 0.2 e sin 2 t y t − = , z t = ,t 0,20 表示的空间曲线. 解 相应的 Matlab 程序为 >>t=0:0.01:20; >>x=exp(-0.2*t).*cos(0.5*pi*t) ; y= exp(-0.2*t).*sin(0.5*pi*t) ; z=t; >>plot3(x,y,z); >>text(x(1),y(1),z(1),'start') ; %在(x(1),y(1),z(1)处加标字符串 'start' >> n=length(x);text(x(n),y(n),z(n),'end') ; %在(x(n),y(n),z(n)处加标字符串 'end' >> xlabel('X');ylabel('Y'),zlabel('Z') ; %说明坐标轴标记 >> grid on; % grid on/grid off 为显示/不显示格栅命令 运行结果如图 6-47

y10 0.6 0.5 06 图6-1 例2作出函数x=me2+在矩形区域-l≤x≤c2,-d机≤y≤d2上的图形,其中 a=b=0.1,cl=c2=5,dl=d2=6. 解相应的Matlab程序为 >》[x,y]=meshgrid(-5:0.1:5,6:0.1:6):%生成自变量矩阵,将坐标(仪,)网格化 >z=0.1*x.*exD(-0.1*(x.“2+y.2): >plot3(x,y,z) 运行后屏幕显示所作的图形如图6-48所示 02 01 5 405 图6-2 二、空间曲面的绘制 Matlab软件中用于绘制曲面的常用网图函数有以下几个: m©sh(x,y,z)用空间中的两组相关的平行平面上的网状线的方式表示曲面 meshc(x,y,z) 用mesh函数的方式表示曲面,并附带有等高线 meshz(x,y,z)屏蔽的网格图
2 图 6-1 例 2 作出函数 2 2 ( ) e b x y x ax − + = 在矩形区域 −c1 ≤ x ≤ c2 , −d1 ≤ y ≤ d 2 上的图形,其中 a b = = 0.1, c c 1 2 5 = = , d d 1 2 6 = = . 解 相应的 Matlab 程序为 >> [x,y]=meshgrid(-5:0.1:5,-6:0.1:6); %生成自变量矩阵,将坐标(X,Y)网格化 >> z=0.1*x.*exp(-0.1*(x.^2+y.^2)); >> plot3(x,y,z) 运行后屏幕显示所作的图形如图 6-48 所示. 图 6-2 二、空间曲面的绘制 Matlab 软件中用于绘制曲面的常用网图函数有以下几个: mesh(x,y,z) meshc(x,y,z) meshz(x,y,z) 用空间中的两组相关的平行平面上的网状线的方式表示曲面 用 mesh 函数的方式表示曲面,并附带有等高线 屏蔽的网格图

surf(x,y,z) 用空间中网状线并网格中填充色彩的方式表示曲面 surfc(x,y,z) 用surf函数的方式表示曲面,并附带有等高线 surfl(x,y,z) 用surf函数的方式表示曲面,并附带有阴影 hidden on 消除掉被遮住部分的网状线 hidden off 将被遮住部分的网状线显示出来 例3画出函数:=√2+了的图形,其中(,y)[-3,3引×-3,3引 解相应的Matlab程序为 >>x=-3:0.1:3: %x的范围为[-3,3引 >》y=-3:0.1:3: %y的范围为[-3,3引 >[X,Y]=meshgrid(x,y) %将向量x,y指定的区域转化为矩阵X,Y >Z=sqrt(X.^2+Y.^2): %产生函数值Z >>mesh(X,Y,Z) 运行结果如图6-49.图6-49是网格线图,如果要画完整的曲面图,只需将上述的Mat1ab代 码mesh(仪,Y,Z)改为surf(仪,Y,Z),运行结果如图6-50. 图6-3 图6-4 如果画等高线,还可以单独调用contour,contour3命令.其中contour命令画二维等 高线,contour3命令画三维等高线.先对上述锥面画二维等高线,相应的Matlab程序为 >x=-3:0.1:3: y=-3:0.1:3: >[X,Y]=meshgrid(x,y):Z=sqrt (X."2+Y.2): >>contour (X.Y.Z.10) %画10条等高线 >>xlabel('X-axis'),ylabel('Y-axis') %坐标轴的标记 >title('Contour of Surface') %加标题 >grid on %画网格线 运行结果如图6-51
3 surf(x,y,z) surfc(x,y,z) surfl(x,y,z) hidden on hidden off 用空间中网状线并网格中填充色彩的方式表示曲面 用 surf 函数的方式表示曲面,并附带有等高线 用 surf 函数的方式表示曲面,并附带有阴影 消除掉被遮住部分的网状线 将被遮住部分的网状线显示出来 例 3 画出函数 2 2 z x y = + 的图形,其中 ( , ) [ 3,3] [ 3,3] x y − − . 解 相应的 Matlab 程序为 >> x=-3:0.1:3; % x 的范围为 [ 3,3] − >> y=-3:0.1:3; % y 的范围为 [ 3,3] − >> [X,Y]=meshgrid(x,y); %将向量 x,y 指定的区域转化为矩阵 X,Y >>Z=sqrt(X.^2+Y.^2); %产生函数值 Z >>mesh(X,Y,Z) 运行结果如图 6-49.图 6-49 是网格线图,如果要画完整的曲面图,只需将上述的 Matlab 代 码 mesh(X,Y,Z)改为 surf(X,Y,Z),运行结果如图 6-50. 图 6-3 图 6-4 如果画等高线,还可以单独调用 contour,contour3 命令.其中 contour 命令画二维等 高线,contour3 命令画三维等高线.先对上述锥面画二维等高线,相应的 Matlab 程序为 >> x=-3:0.1:3; y=-3:0.1:3; >> [X,Y]=meshgrid(x,y); Z=sqrt(X.^2+Y.^2); >>contour(X,Y,Z,10) %画 10 条等高线 >>xlabel('X-axis'),ylabel('Y-axis') %坐标轴的标记 >> title('Contour of Surface') %加标题 >> grid on %画网格线 运行结果如图 6-51
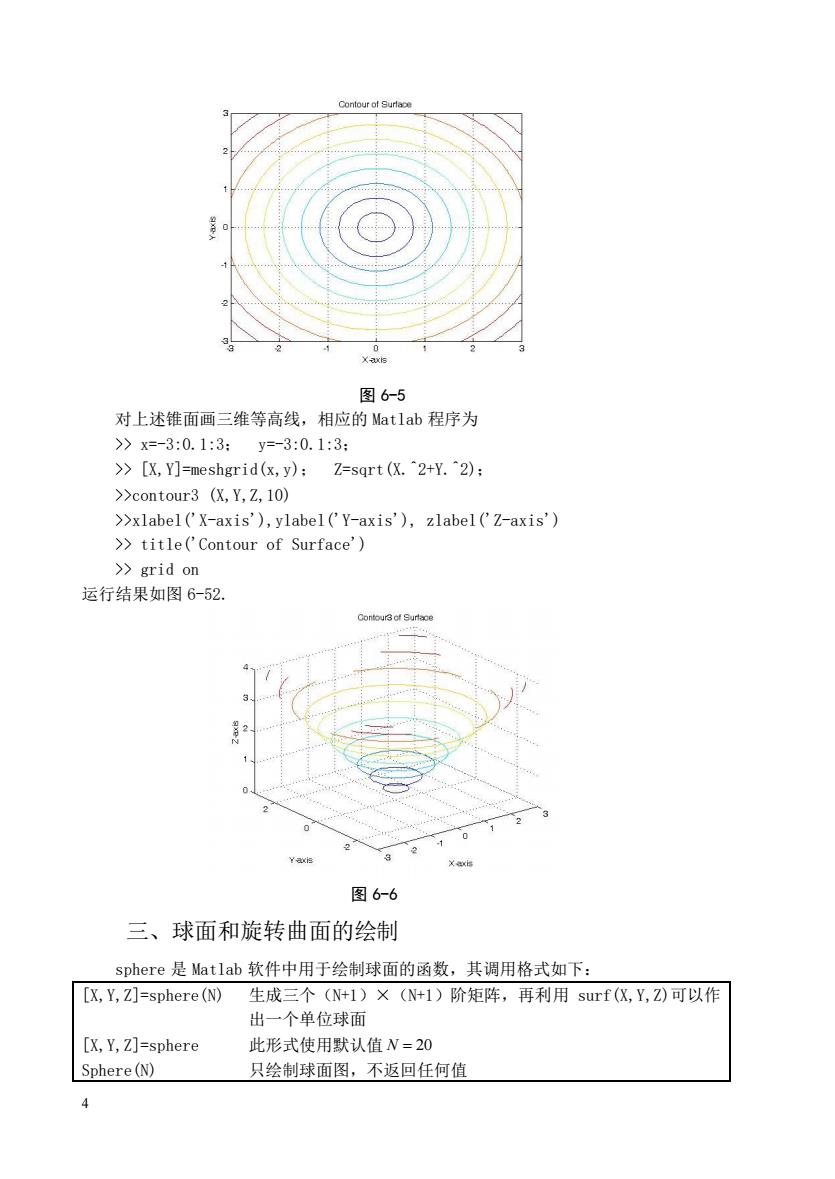
ur of s 图6-5 对上述锥面画三维等高线,相应的Matlab程序为 >x=-3:0.1:3: y=-3:0.1:3: >[X,Y]=meshgrid(x,y):Z=sqrt (X.2+Y.2); >>contour3 (X,Y,Z,10) >>xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis') >>title('Contour of Surface') >grid on 运行结果如图6-52, 图6-6 三、球面和旋转曲面的绘制 sphere是Matlab软件中用于绘制球面的函数,其调用格式如下: [X,Y,Z]=sphere(N) 生成三个(N+1)×(N+1)阶矩阵,再利用surf(仪,Y,Z)可以作 出一个单位球面 [X,Y,Z]=sphere 此形式使用默认值N=20 Sphere(N) 只绘制球面图,不返回任何值
4 图 6-5 对上述锥面画三维等高线,相应的 Matlab 程序为 >> x=-3:0.1:3; y=-3:0.1:3; >> [X,Y]=meshgrid(x,y); Z=sqrt(X.^2+Y.^2); >>contour3 (X,Y,Z,10) >>xlabel('X-axis'),ylabel('Y-axis'), zlabel('Z-axis') >> title('Contour of Surface') >> grid on 运行结果如图 6-52. 图 6-6 三、球面和旋转曲面的绘制 sphere 是 Matlab 软件中用于绘制球面的函数,其调用格式如下: [X,Y,Z]=sphere(N) [X,Y,Z]=sphere Sphere(N) 生成三个(N+1)×(N+1)阶矩阵,再利用 surf(X,Y,Z)可以作 出一个单位球面 此形式使用默认值 N = 20 只绘制球面图,不返回任何值

cylinder是Matlab软件中用于绘制旋转曲面的函数,其调用格式如下 [X,Y,Z]=cylinder(R,)以母线向量R生成单位柱面,母线向量R在单位高度 里等分刻度上定义的半径向量,N为旋转圆周上的分格线的务 数,再利用surf(X,Y,Z)可作出一个旋转面 [X,Y,Z]=cylinder (R) 此形式使用默认值N=20和R=[1,1] 或[X,Y,Z]=cylinder 例4输入下列Mat1ab程序 >>[a,b,c]=sphere(30); >surf(a,b,c) >axis'equal'),axis'square')%将横、纵、竖坐标的刻度控制为相同 运行后输出球面如图6-53. 四、综合作图 我们可以综合使用上面介绍的方法,作平 05 面区域和空间区域的图形,下面将通过一些具 体的例题来介绍. 例5画出由旋转抛物面:=8-x2-y2,圆柱 05 面x2+y=4和坐标面:=0所围成的空间闭 040 05 05 区域及其在xOy面上的投影. 解相应的Matlab程序为 图6-7 >[x,y]=meshgrid(-2:0.01:2): >》z1=8-x.^2-y.^2: >>figure(1) >>meshc(x,y,21) >hold on >x=-2:0.01:2: >》r=2: >[x,y,z]=cylinder(r,30); >mesh(x.v.z) >>hold off >>figure(2) >contour(x,y,2,10) axis(equal'),axis('square') 运行后屏幕显示如图6-54、图6-55所示
5 cylinder 是 Matlab 软件中用于绘制旋转曲面的函数,其调用格式如下: [X,Y,Z]=cylinder(R,N) [X,Y,Z]=cylinder(R) 或 [X,Y,Z]=cylinder 以母线向量 R 生成单位柱面,母线向量 R 在单位高度 里等分刻度上定义的半径向量,N 为旋转圆周上的分格线的条 数,再利用 surf(X,Y,Z)可作出一个旋转面 此形式使用默认值 N = 20 和 R=[1,1] 例 4 输入下列 Matlab 程序 >> [a,b,c]=sphere(30); >> surf(a,b,c); >>axis('equal'),axis('square') %将横、纵、竖坐标的刻度控制为相同 运行后输出球面如图 6-53. 四、综合作图 我们可以综合使用上面介绍的方法,作平 面区域和空间区域的图形,下面将通过一些具 体的例题来介绍. 例 5 画出由旋转抛物面 2 2 z x y = − − 8 ,圆柱 面 2 2 x y + = 4 和坐标面 z = 0 所围成的空间闭 区域及其在 xOy 面上的投影. 解 相应的 Matlab 程序为 图 6-7 >> [x,y]=meshgrid(-2:0.01:2); >> z1=8-x.^2-y.^2; >> figure(1) >> meshc(x,y,z1) >> hold on >> x=-2:0.01:2; >> r=2; >> [x,y,z]=cylinder(r,30); >> mesh(x,y,z) >> hold off >> figure(2) >> contour(x,y,z,10) axis('equal'),axis('square') 运行后屏幕显示如图 6-54、图 6-55 所示

图6-8 图69 例6画出马鞍面:=x2-2y2和平面:=2x-3y的交线 解相应的Matlab程序为 >[x,y=meshgrid(-52:2:52: >z1=x.^2-2*灯.^2: 4000 >》z2=2*x-3*y 200 >>mesh(x,y,z1) 0 >hold on 200 >>mesh(x,y,22) >hold off 运行后屏幕显示如图6-56. .10m.1m 图6-10 6
6 图 6-8 图 6-9 例 6 画出马鞍面 2 2 z x y = − 2 和平面 z x y = − 2 3 的交线. 解 相应的 Matlab 程序为 >> [x,y]=meshgrid(-52:2:52; >> z1=x.^2-2*y.^2; >> z2=2*x-3*y; >> mesh(x,y,z1) >> hold on >> mesh(x,y,z2) >> hold off 运行后屏幕显示如图 6-56. 图 6-10