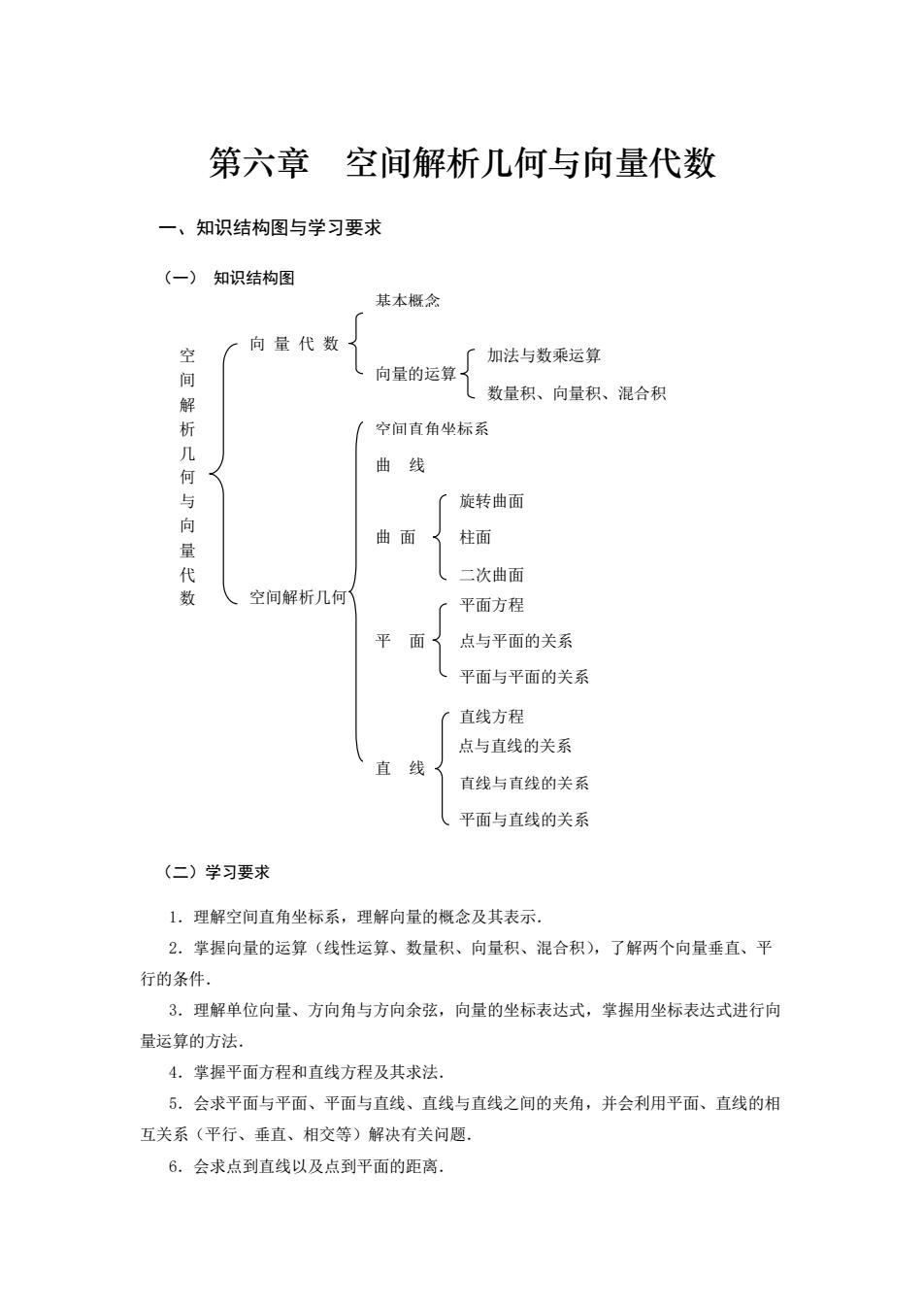
第六章 空间解析几何与向量代数 一、知识结构图与学习要求 (一)知识结构图 基本概念 空 向量代数 「加法与数乘运算 间 向量的运算 数量积、向量积、混合积 空间直角坐标系 曲线 何 与 了旋转曲面 曲面 柱面 ,二次曲面 数 空间解析几何 平面方程 面 点与平面的关系 平面与平面的关系 直线方程 点与直线的关系 直线 直线与直线的关系 平面与直线的关系 (二)学习要求 1.理解空间直角坐标系,理解向量的概念及其表示。 2.掌握向量的运算(线性运算、数量积、向量积、混合积),了解两个向量垂直、平 行的条件 3.理解单位向量、方向角与方向余弦,向量的坐标表达式,掌握用坐标表达式进行向 量运算的方法 4.掌握平面方程和直线方程及其求法. 5.会求平面与平面、平面与直线、直线与直线之间的夹角,并会利用平面、直线的相 互关系(平行、垂直、相交等)解决有关问题, 6.会求点到直线以及点到平面的距离
第六章 空间解析几何与向量代数 一、知识结构图与学习要求 (一) 知识结构图 (二)学习要求 1.理解空间直角坐标系,理解向量的概念及其表示. 2.掌握向量的运算(线性运算、数量积、向量积、混合积),了解两个向量垂直、平 行的条件. 3.理解单位向量、方向角与方向余弦,向量的坐标表达式,掌握用坐标表达式进行向 量运算的方法. 4.掌握平面方程和直线方程及其求法. 5.会求平面与平面、平面与直线、直线与直线之间的夹角,并会利用平面、直线的相 互关系(平行、垂直、相交等)解决有关问题. 6.会求点到直线以及点到平面的距离. 空 间 解 析 几 何 与 向 量 代 数 平面方程 数量积、向量积、混合积 空间解析几何 加法与数乘运算 向 量 代 数 点与平面的关系 平面与平面的关系 平 面 曲 面 空间直角坐标系 直 线 直线方程 平面与直线的关系 点与直线的关系 重心坐标 直线与直线的关系 二次曲面 曲 线 基本概念 旋转曲面 柱面 向量的运算

7.了解曲面方程和空间曲线方程的概念· 8.了解常用二次曲面的方程及其图形,会求以坐标轴为旋转轴的旋转曲面及母线平行 于坐标轴的柱面方程。 9。了解空间曲线的参数方程和一般方程。了解空间曲线在坐标平面上的投影,并会求 其方程 二、内容提要 (一)向量 1.基本概念 (1)向量是指既有大小又有方向的量,或以小写字母表示,或者以空间有向线段的 起点与终点表示,如AB表示以A为起点,B为终点的向量. (2)向量a的大小称为向量a的模,记为al (3)两个向量相等指其大小相等且方向相同. (4)模等于1的向量称为单位向量:模等于0的向量称为零向量,且规定其方向是任 意的:与a大小相等且方向相反的向量称为a的负向量,记作-a. 2.向量平行与向量的坐标 (1)设a,b为非零向量,若其方向相同或相反,则称向量a与b平行,记为a∥b.特 别地,规定零向量与任何向量都平行. (2)使向量a的起点与空间直角坐标系的原点重合,称向量的终点坐标(x,,) 为向量a的坐标,记为(x,),且有1a非√F+y严+F 3.方向角与方向余弦 (1)非零向量a与三个坐标轴r轴、y轴、:轴正向的夹角a,B,y称为向量a的方 向角,且a,B,y∈0,π].称cosa,cosB,cosy为向量a的方向余弦.以向量a的方向余弦为坐 标的向量即为与a同方向的单位向量e。,且 cosa+coB+cos=1,e=(cosa.cos B.cos). (2)若a=(x,y,),则有 4.向量在轴上的投影 (I)定义:设向量a与轴u的夹角为p,则称alcos为向量a在u轴上的投影,记 为Prja或(a. (2)性质:
7.了解曲面方程和空间曲线方程的概念. 8.了解常用二次曲面的方程及其图形,会求以坐标轴为旋转轴的旋转曲面及母线平行 于坐标轴的柱面方程. 9.了解空间曲线的参数方程和一般方程.了解空间曲线在坐标平面上的投影,并会求 其方程. 二、内容提要 (一)向量 1.基本概念 (1)向量是指既有大小又有方向的量,或以小写字母 a 表示,或者以空间有向线段的 起点与终点表示,如 AB 表示以 A 为起点, B 为终点的向量. (2)向量 a 的大小称为向量 a 的模,记为 | | a . (3)两个向量相等指其大小相等且方向相同. (4)模等于 1 的向量称为单位向量;模等于 0 的向量称为零向量,且规定其方向是任 意的;与 a 大小相等且方向相反的向量称为 a 的负向量,记作−a . 2.向量平行与向量的坐标 (1)设 ab, 为非零向量,若其方向相同或相反,则称向量 a 与 b 平行,记为 a b // .特 别地,规定零向量与任何向量都平行. (2)使向量 a 的起点与空间直角坐标系的原点重合,称向量 a 的终点坐标 ( , , ) x y z 为向量 a 的坐标,记为 ( , , ) x y z ,且有 2 2 2 | | a = + + x y z . 3.方向角与方向余弦 (1)非零向量 a 与三个坐标轴 x 轴、 y 轴、 z 轴正向的夹角 , , 称为向量 a 的方 向角,且 , , [0, ] .称 cos ,cos ,cos 为向量 a 的方向余弦.以向量 a 的方向余弦为坐 标的向量即为与 a 同方向的单位向量 a e ,且 2 2 2 cos cos cos 1 + + = , = (cos ,cos ,cos ) a e . (2)若 a = ( , , ) x y z ,则有 2 2 2 cos x x y z = + + , 2 2 2 cos y x y z = + + , 2 2 2 cos z x y z = + + . 4.向量在轴上的投影 (1)定义:设向量 a 与轴 u 的夹角为 ,则称 | | cos a 为向量 a 在 u 轴上的投影,记 为 Pr j u a 或 ( ) u a . (2)性质:

a.Prja-al-coso, b.Prj.(a+az)=Prja+Prj.az' c.Prj.(Za)=APrja (3)向量a在与其方向相同的轴上的投影为其模a小.在空间直角坐标系下,:在各 坐标轴的投影即为向量a的坐标x,y,:,则向量a可表成a=d+以+k. 5.向量的线性运算及其性质 (1)加减法运算: 向量加法运算遵循平行四边形法则或三角形法则。 设a=(,b=(3,),则 a±b=(g±x,3±为,5±) (2)数乘运算: 向量a与实数2的乘积,记为a.设a=(x,y),则 a=(2x,ya), 且2a的方向为:当>0时,2a与a方向相同: 当无<0时,a与a方向相反: 当元=0时,和为零向量,方向任意. a的模:liaHal-la, (3)性质: a.a+b=b+a,(a+b)+c=a+(b+c). b.2ua)=0)=(r)a,(+)a=a+n,(a+b=2a+b. c.设a为非零向量,则b∥a一存在唯一实数入,使b=2a. 6.两个向量的数量积 向量a与向量b的数量积定义为 a.bal-lblcos(a,b) 由此可知a上√aa. (1)在空间直角坐标系下,若a=(:,片,),b=(,片,),则 ab=x++的: 且对于非零向量a与向量b的夹角(a,b)满足 a.b xx3+片y2+52 osa.=a1++++ 由此可知: a1b白ab=0台x+y+52=0, (2)向量的数量积的投影表示:
a. Pr j | | cos u a a = , b. Pr j ( ) Pr j Pr j u u u a a a a 1 2 1 2 + = + , c. Pr j ( ) Pr j u u a a = . (3)向量 a 在与其方向相同的轴上的投影为其模 | | a .在空间直角坐标系下,a 在各 坐标轴的投影即为向量 a 的坐标 x y z , , ,则向量 a 可表成 a i j k = + + x y z . 5.向量的线性运算及其性质 (1)加减法运算: 向量加法运算遵循平行四边形法则或三角形法则. 设 1 1 1 a = ( , , ) x y z , 2 2 2 b = ( , , ) x y z ,则 1 2 1 2 1 2 a b = ( , , ) x x y y z z . (2)数乘运算: 向量 a 与实数 的乘积,记为 a .设 a = ( , , ) x y z ,则 a = ( , , ) x y z , 且 a 的方向为:当 0 时, a 与 a 方向相同; 当 0 时, a 与 a 方向相反; 当 = 0 时, a 为零向量,方向任意. a 的模:| | | | | | a a = , (3)性质: a. a b b a + = + , ( ) ( ) a b c a b c + + = + + . b. ( ) ( ) ( ) a a a = = ,( ) + = + a a a , ( ) a b a b + = + . c.设 a 为非零向量,则 b a // 存在唯一实数 ,使 b a = . 6.两个向量的数量积 向量 a 与向量 b 的数量积定义为: a b a b a b = | | | | cos , ( ), 由此可知 | | a a a = . (1)在空间直角坐标系下,若 1 1 1 a = ( , , ) x y z , 2 2 2 b = ( , , ) x y z ,则 1 2 1 2 1 2 a b = + + x x y y z z , 且对于非零向量 a 与向量 b 的夹角 (a b, ) 满足 1 2 1 2 1 2 2 2 2 2 2 2 1 1 1 2 2 2 cos , | | | | x x y y z z x y z x y z + + = = + + + + ( ) a b a b a b , 由此可知: 1 2 1 2 1 2 a b a b ⊥ = + + = 0 0 x x y y z z . (2)向量的数量积的投影表示:

a.b=bPria日alPrib (3)数量积满足下列运算规律: a.交换律:a-b=b-a b.分配律:(a+b)-c=ac+bc. c.结合律:(2a)b=(ab),其中2为实数 7.两个向量的向量积 向量a与向量b的向量积a×b是一个新的向量,其模为absin(a,b),方向垂直于 a、b,其指向按右手规则从a转向b来确定. (1)在空间直角坐标系下,若a=(:,片,),b=(3,乃,-),则 i jk a×b=片马 由此可知: aWb白a×b=0台立=当=互,特别地a×a=0 (2)向量积的几何意义: 以向量a与b为邻边的平行四边形的面积 S=曰a×b 以向量a与b为邻边的三角形的面积 S-laxbl. (3)向量积满足下列运算规律: a.反交换律:b×a=-a×b: b.结合律:(a)×b=ax(2b)=(a×b),其中元为实数 c.分配律:(a+b)xc=axe+bxc, 8.三个向量的混合积 称(a×b)c为向量a、五、c的混合积,记为[abc]· (1)在直角坐标系下,若a=(,),b=(,片,),c=(:,),则 片 且有如下常用结论: 向量、bc共面存在常数乙,4,使
| | Pr j | | Pr j b a a b b a a b = = . (3)数量积满足下列运算规律: a.交换律: a b b a = . b.分配律: ( ) a b c a c b c + = + . c.结合律: ( ) ( ) a b a b = ,其中 为实数. 7.两个向量的向量积 向量 a 与向量 b 的向量积 a b 是一个新的向量,其模为 | | | | sin , a b a b ( ) ,方向垂直于 a 、 b ,其指向按右手规则从 a 转向 b 来确定. (1)在空间直角坐标系下,若 1 1 1 a = ( , , ) x y z , 2 2 2 b = ( , , ) x y z ,则 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 y z x z x y x y z y z x z x y x y z = = − + i j k a b i j k , 由此可知: 1 1 1 2 2 2 // x y z x y z a b a b = = = 0 ,特别地 a a = 0 . (2)向量积的几何意义: 以向量 a 与 b 为邻边的平行四边形的面积 S = | | a b . 以向量 a 与 b 为邻边的三角形的面积 1 | | 2 S = a b . (3)向量积满足下列运算规律: a.反交换律: b a = − a b ; b.结合律: ( ) ( ) ( ) a b a b a b = = ,其中 为实数; c.分配律: ( ) a b c a c b c + = + . 8.三个向量的混合积 称 ( ) a b c 为向量 a b c 、 、 的混合积,记为 [ ] abc . (1)在直角坐标系下,若 1 1 1 a = ( , , ) x y z , 2 2 2 b = ( , , ) x y z , 3 3 3 c = ( , , ) x y z ,则 1 1 1 2 2 2 3 3 3 [ ] x y z x y z x y z abc = , 且有如下常用结论: 向量 a b c 、 、 共面 存在常数 , ,使

c=aa+ub台[abc=0台 =0 馬乃 (2)混合积的几何意义: (ax)c的绝对值在数值上等于以向量a、c为棱的平行六面体的体积,即 V(axb)-cl. (3)混合积的性质: [abe]=[cab]=[beal,[abe]=-bac]=-cba]=-acb]. (二)曲面与曲线 1.空间曲面方程 a.一般方程:F(x,y)=0: b.显式方程:=fx,y): c.参数方程 「x=xu,) y=Mu,v) =u,y) 其中(u,)eD,D为m平面上某一区域。 2.旋转曲面方程 设C:fy,)=0为O平面上的曲线,则C绕:轴旋转所得的曲面 f±2+y2,)=0 C绕y轴旋转所得的曲面为 f0y,±2+2)=0. 其它坐标面上的曲线绕相应坐标轴旋转的情形完全类似,旋转曲面主要由母线和旋转轴确 定 3.柱面方程 母线平行于:轴的柱面方程为F(x,y)=0:母线平行于x轴的柱面方程为G以,)=0: 母线平行于y轴的柱面方程为H(x,)=0.当曲面方程中缺少一个变量时,则曲面为柱面.柱 面方程须注意准线和母线两个要素。 4.常见的二次曲面 (1)球面方程(x-子+心-为+-2=R,其中(3)为球心,R>0为 球的半径. (2)球面方程等++号=a>06>0c>0),当a=b=c时,即为球面方程 12 -2
c a b = + = [ ] 0 abc 1 1 1 2 2 2 3 3 3 0 x y z x y z x y z = . (2)混合积的几何意义: ( ) a b c 的绝对值在数值上等于以向量 a b c 、 、 为棱的平行六面体的体积,即 V = | ( ) | a b c . (3)混合积的性质: [ ] [ ] [ ] abc cab bca = = ,[ ] [ ] [ ] [ ] abc bac cba acb = − = − = − . (二)曲面与曲线 1.空间曲面方程 a.一般方程: F x y z ( , , ) 0 = ; b.显式方程: z f x y = ( , ) ; c.参数方程 ( , ) ( , ) ( , ) x x u v y y u v z z u v = = = 其中 ( , ) u v D , D 为 uv 平面上某一区域. 2.旋转曲面方程 设 C f y z : ( , ) 0 = 为 yOz 平面上的曲线,则 C 绕 z 轴旋转所得的曲面 2 2 f x y z ( , ) 0 + = , C 绕 y 轴旋转所得的曲面为 2 2 f y x z ( , ) 0 + = . 其它坐标面上的曲线绕相应坐标轴旋转的情形完全类似,旋转曲面主要由母线和旋转轴确 定. 3.柱面方程 母线平行于 z 轴的柱面方程为 F x y ( , ) 0 = ;母线平行于 x 轴的柱面方程为 G y z ( , ) 0 = ; 母线平行于 y 轴的柱面方程为 H x z ( , ) 0 = .当曲面方程中缺少一个变量时,则曲面为柱面.柱 面方程须注意准线和母线两个要素. 4.常见的二次曲面 (1)球面方程 2 2 2 2 0 0 0 ( ) ( ) ( ) x x y y z z R − + − + − = ,其中 0 0 0 ( , , ) x y z 为球心, R 0 为 球的半径. (2)椭球面方程 2 2 2 2 2 2 1( 0, 0, 0) x y z abc a b c + + = ,当 abc = = 时,即为球面方程.

(3)单叶双曲面方程 其中a>0,b>0,c>0,即系数两项为正,一项为负。 (4)双叶双曲面方程 其中a>0,b>0,c>0,即系数两项为负,一项为正。 (5)椭圆抛物面方程 12-2 (6)双曲抛物面方程(又称为马鞍面) (7)圆柱面方程 x2+y2=R2或y+2=R2或x2+2=R2(R>0) (8)椭圆柱面方程 号+若1攻若+号1成若+号1o>06>0c>0 (9)双曲柱面方程 手-若-1政手-号成岁-1a>06>0c>0, (10)抛物柱面方程 =2m或y=2px,y=2pr或2=2pm,2=2pm或x=-2 其中p为非零实数。 5.空间曲线 (1)空间曲线两种表示形式: 一般方程∫Fx5)=O [x=x) Gxy=)=0 和参数方程 (2)空间曲线在坐标面上的投影:求投影曲线方程的方法是先求出空间曲线在给定平 面上的投影柱面方程,然后将投影柱面方程与给定平面方程联立,即求得投影曲线方程。 (三)平面 1.平面方程 (1)点法式方程:4x-x)+B心y-)+C(e-)=0,其中P(x,%,)为平面上已知 点,n=(A,B,C)为平面的法向量
(3)单叶双曲面方程 2 2 2 2 2 2 1 x y z a b c + − = 或 2 2 2 222 1 x y z a b c − + = 或 2 2 2 2 2 2 1 x y z a b c − + + = . 其中 abc 0, 0, 0 ,即系数两项为正,一项为负. (4)双叶双曲面方程 2 2 2 2 2 2 1 x y z a b c − − = 或 2 2 2 2 2 2 1 y x z b a c − − = 或 2 2 2 2 2 2 1 z x y c a b − − = . 其中 abc 0, 0, 0 ,即系数两项为负,一项为正. (5)椭圆抛物面方程 2 2 2 2 x y z a b = + 或 2 2 2 2 x z y a c = + 或 2 2 2 2 y z x b c = + ( 0, 0, 0) abc . (6)双曲抛物面方程(又称为马鞍面) 2 2 2 2 ( ) x y z a b = + 或 2 2 2 2 ( ) x z y a c = − 或 2 2 2 2 ( ) y z x b c = + ( 0, 0, 0) abc . (7)圆柱面方程 2 2 2 x y R + = 或 2 2 2 y z R + = 或 2 2 2 x z R + = ( 0) R . (8)椭圆柱面方程 2 2 2 2 1 x y a b + = 或 2 2 2 2 1 x z a c + = 或 2 2 2 2 1 y z b c + = ( 0, 0, 0) abc . (9)双曲柱面方程 2 2 2 2 1 x y a b − = 或 2 2 2 2 1 x z a c − = 或 2 2 2 2 1 y z b c − = ( 0, 0, 0) abc . (10)抛物柱面方程 2 x py = 2 或 2 y px = 2 , 2 y pz = 2 或 2 z py = 2 , 2 z px = 2 或 2 x pz = 2 , 其中 p 为非零实数. 5.空间曲线 (1)空间曲线两种表示形式: 一般方程 ( , , ) 0 ( , , ) 0 F x y z G x y z = = 和参数方程 ( ) ( ) ( ) x x t y y t z z t = = = . (2)空间曲线在坐标面上的投影:求投影曲线方程的方法是先求出空间曲线在给定平 面上的投影柱面方程,然后将投影柱面方程与给定平面方程联立,即求得投影曲线方程. (三)平面 1.平面方程 (1)点法式方程: 0 0 0 A x x B y y C z z ( ) ( ) ( ) 0 − + − + − = ,其中 0 0 0 P x y z ( , , ) 为平面上已知 点, n = ( , , ) A B C 为平面的法向量.

(2)一般式方程:Ar++C-+D=0,其中n=(4B,C)为平面的法向量. (3)截距式方程:+兰+三=1,其中a,bc分别为平面在x:轴上的截距.由于要 求a,6.c非零,故并非所有平面均可表示成这种形式。 2.平面之间的关系 若平面元:4x+By+C:+D=0,元2:4x+B,y+C,:+D,=0,则两平面法向量%, 的夹角(取锐角)称为平面元,与,的夹角,记为日,且 c0s0=4·久1 44+BB+CC m川%√++CG√G+房+CG 由上可知, 当0-0时、平与元平行(合重合)台冬-叠-会 (2)当8=时,平面元,与石垂直口A4+BB+CC=0. 3.平面束方程 设平面π:Ax+By+C:+D=0,元2:4x+By+C,:+D,=0,若平面元,与0,不平行, 且其交线为1,则过1的所有平面方程可表示为 (4x+By+CF+D)+4(4r+By+C+D,)=0, 其中乙,4eR,称这样一族平面为过直线1的平面束。特别地,若元=1,则 Ax+By+C=+D+x+By+C:+D)=0 (HER) 表示除平面元外,过1的所有其它平面的方程. (四)直线 1.直线方程 Ax+By+Cz+D=0 (1)一般方程: 4x+y+C:+=0记%=(4.G),%=4,民,C,则直 线的方向向量可取为s=,×,· Q)对称式方程(点向式方程:片.之-号,其中x)为直线上给 定的已知点,=(m,P)为直线的方向向量 [x=6+m (3)参数方程:{y=%+H,其中1∈R且Px,)为直线上已知点,5=(m,np) (==50+pt 为直线的方向向量 直线的上述三种方程可互相转化 2.点、直线、平面之间的关系
(2)一般式方程: Ax By Cz D + + + = 0 ,其中 n = ( , , ) A B C 为平面的法向量. (3)截距式方程: 1 x y z a b c + + = ,其中 abc , , 分别为平面在 x y z , , 轴上的截距.由于要 求 abc , , 非零,故并非所有平面均可表示成这种形式. 2.平面之间的关系 若平面 1 1 1 1 1 : 0 A x B y C z D + + + = , 2 2 2 2 2 : 0 A x B y C z D + + + = ,则两平面法向量 1 2 n n, 的夹角(取锐角)称为平面 1 与 2 的夹角,记为 ,且 1 2 1 2 1 2 1 2 2 2 2 2 2 2 1 2 1 1 1 2 2 2 | | cos | | | | A A B B C C A B C A B C + + = = + + + + n n n n , 由上可知, (1)当 = 0 时,平面 1 与 2 平行(含重合) 1 1 1 2 2 2 A B C A B C = = ; (2)当 2 = 时,平面 1 与 2 垂直 1 2 1 2 1 2 + + = A A B B C C 0 . 3.平面束方程 设平面 1 1 1 1 1 : 0 A x B y C z D + + + = , 2 2 2 2 2 : 0 A x B y C z D + + + = ,若平面 1 与 2 不平行, 且其交线为 l ,则过 l 的所有平面方程可表示为 1 1 1 1 2 2 2 2 ( ) ( ) 0 A x B y C z D A x B y C z D + + + + + + + = , 其中 , R ,称这样一族平面为过直线 l 的平面束.特别地,若 =1 ,则 1 1 1 1 2 2 2 2 A x B y C z D A x B y C z D R + + + + + + + = ( ) 0 ( ) 表示除平面 2 外,过 l 的所有其它平面的方程. (四)直线 1.直线方程 (1)一般方程: 1 1 1 1 2 2 2 2 0 0 A x B y C z D A x B y C z D + + + = + + + = .记 1 1 1 1 n = ( , , ) A B C , 2 2 2 2 n = ( , , ) A B C ,则直 线的方向向量可取为 = 1 2 s n n . (2)对称式方程(点向式方程): 0 0 0 x x y y z z m n p − − − = = ,其中 0 0 0 P x y z ( , , ) 为直线上给 定的已知点, s = ( , , ) m n p 为直线的方向向量. (3)参数方程: 0 0 0 x x mt y y nt z z pt = + = + = + ,其中 t R 且 0 0 0 P x y z ( , , ) 为直线上已知点, s = ( , , ) m n p 为直线的方向向量. 直线的上述三种方程可互相转化. 2.点、直线、平面之间的关系

(1)两条直线之间的关系 、设有线一-兰=,:是=之=产,且其方向向量分别为 。=(m,%,)和s=(m,m,P),两直线的夹角是指两直线的方向向量、s,之间的夹角(取 锐角)记为日.则 mm+n凸+PP凸L 川西底+所+屏所+四+店0≤≤ 由此可知: a.两直线平行(含重合):4,%==A∥5 m n Pa b.两直线垂直:人⊥h台mm+%h+乃P2=0一禹1马: c.两直线共面:若B,B分别为直线4,上的两点,则 4,4共面台B(s×马2)=0 d.两直线异面: 4,异面台P×5)≠0. (2)直线与平面的关系 已知平面:+y+C+D=0与直线1:-=-业=-,其中n=(4BC, m nD s=(m,np),则直线与平面的夹角定义为:当直线与平面不垂直时,直线1与其在平面π上 的投影直线r的夹角(取锐角)称为直线与平面的夹角,记为6,且 0品品7e2700 1Am+Bn+Cpl 由此可知: a,若直线与平面垂直,则有 Lr台合8-分aa b.若直线与平面平行,则有 IWπ台Am+Bn+Cp=0白s⊥n. (3)距离公式 。点到直线的距离:设给定点化火及直线1:片片产,片,则儿到直 线1的距离为d=PPx到 IsI 其中G,)为直线上任意一点,5=(m儿P)为直线的方向向量
(1)两条直线之间的关系 设直线 1 1 1 1 1 1 1 : x x y y z z l m n p − − − = = , 2 2 2 2 2 2 2 : x x y y z z l m n p − − − = = ,且其方向向量分别为 1 1 1 1 s = ( , , ) m n p 和 2 2 2 2 s = ( , , ) m n p ,两直线的夹角是指两直线的方向向量 1 s 、 2 s 之间的夹角(取 锐角)记为 .则 1 2 1 2 1 2 1 2 2 2 2 2 2 2 1 2 1 1 1 2 2 2 | | | | cos | | | | m m n n p p m n p m n p + + = = + + + + s s s s (0 ) 2 . 由此可知: a.两直线平行(含重合): 1 1 1 1 2 1 2 2 2 2 // // m n p l l m n p = = s s . b.两直线垂直: 1 2 1 2 1 2 1 2 1 2 l l m m n n p p ⊥ + + = ⊥ 0 s s . c.两直线共面:若 1 2 P P, 分别为直线 1 2 l l, 上的两点,则 1 2 l l, 共面 1 2 1 2 = PP ( ) 0 s s . d.两直线异面: 1 2 l l, 异面 1 2 1 2 PP ( ) 0 s s . (2)直线与平面的关系 已知平面 : 0 Ax By Cz D + + + = 与直线 0 0 0 : x x y y z z l m n p − − − = = ,其中 n = ( , , ) A B C , s = ( , , ) m n p ,则直线与平面的夹角定义为:当直线与平面不垂直时,直线 l 与其在平面 上 的投影直线 l 的夹角(取锐角)称为直线与平面的夹角,记为 ,且 2 2 2 2 2 2 | | | | sin (0 ) | | | | 2 Am Bn Cp A B C m n p + + = = + + + + s n s n . 由此可知: a.若直线与平面垂直,则有 // A B C l m n p ⊥ = = s n. b.若直线与平面平行,则有 l Am Bn Cp // 0 + + = ⊥s n. (3)距离公式 a.点到直线的距离:设给定点 0 0 0 0 P x y z ( , , ) 及直线 1 1 1 : x x y y z z l m n p − − − = = ,则 P0 到直 线 l 的距离为 0 1 | | | | P P d = s s , 其中 1 1 1 1 P x y z ( , , ) 为直线上任意一点, s = ( , , ) m n p 为直线的方向向量.

b.点到平面的距离:设给定点Px,)及平面x:k+y+C+D=0,则B到x的 距离为: d=+,+C+0 √R+B+C
b.点到平面的距离:设给定点 0 0 0 P x y z ( , , ) 及平面 : 0 Ax By Cz D + + + = ,则 P0 到 的 距离为: 0 0 0 2 2 2 Ax By Cz D d A B C + + + = + + .