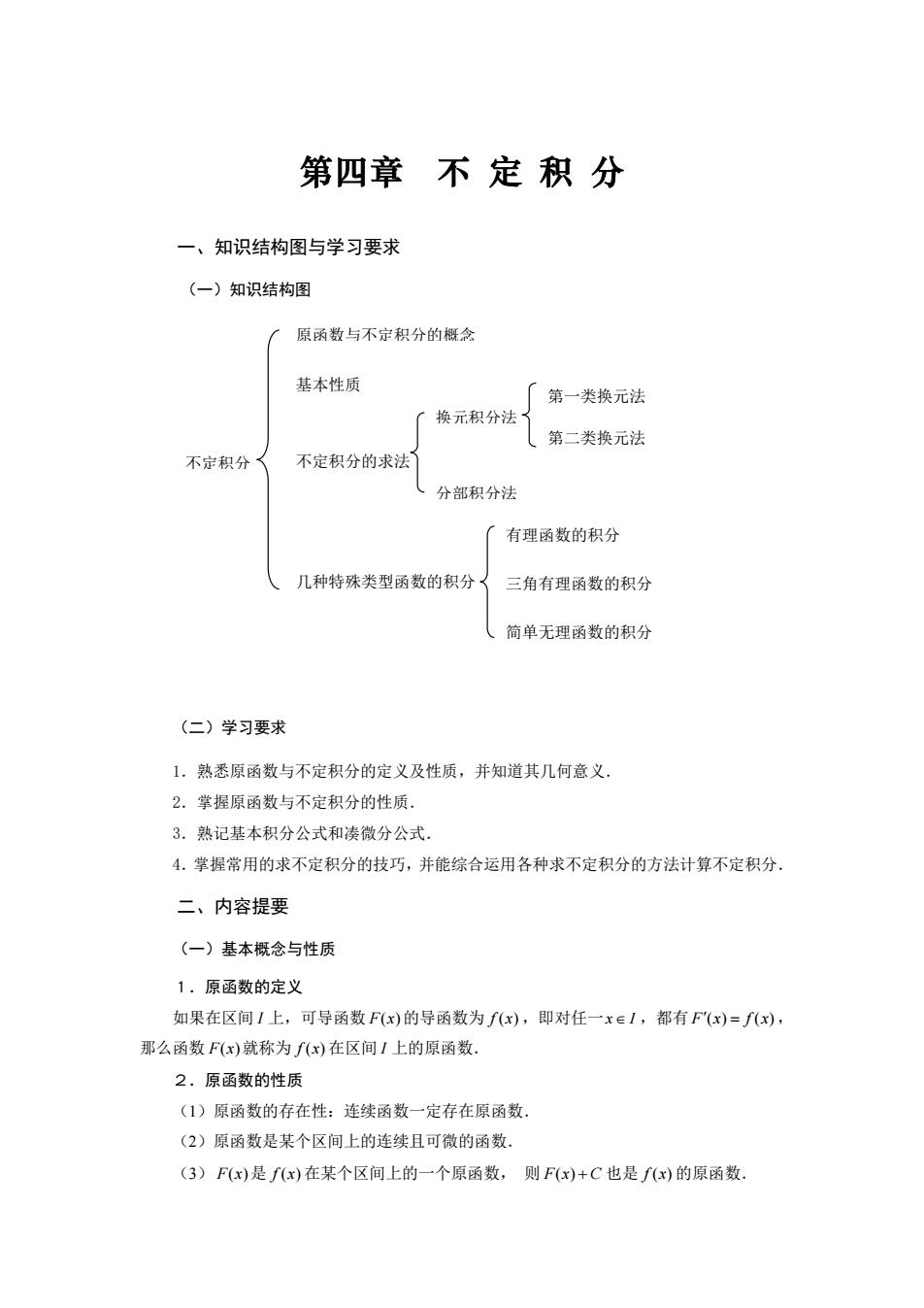
第四章不定积分 一、知识结构图与学习要求 (一)知识结构图 「原函数与不定积分的概念 基本性质 [第一类换元法 换元积分法 (第二类换元法 不定积分 不定积分的求法 (分部积分法 有理函数的积分 几种特殊类型函数的积分 角有理函数的积分 、简单无理函数的积分 (二)学习要求 1.熟悉原函数与不定积分的定义及性质,并知道其几何意义 2.掌握原函数与不定积分的性质. 3.熟记基本积分公式和凑微分公式。 4.掌握常用的求不定积分的技巧,并能综合运用各种求不定积分的方法计算不定积分。 二、内容提要 (一)基本概念与性质 1.原函数的定义 如果在区间1上,可导函数F(x)的导函数为fx),即对任一x∈1,都有F(x)=fx), 那么函数F(x)就称为fx)在区间1上的原函数. 2.原函数的性质 (1)原函数的存在性:连续函数一定存在原函数, (2)原函数是某个区间上的连续且可微的函数. (3)F(x)是f(x)在某个区间上的一个原函数,则Fx)+C也是fx)的原函数
第四章 不 定 积 分 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.熟悉原函数与不定积分的定义及性质,并知道其几何意义. 2.掌握原函数与不定积分的性质. 3.熟记基本积分公式和凑微分公式. 4.掌握常用的求不定积分的技巧,并能综合运用各种求不定积分的方法计算不定积分. 二、内容提要 (一)基本概念与性质 1.原函数的定义 如果在区间 I 上,可导函数 F x( ) 的导函数为 f x( ) ,即对任一 x I ,都有 F x f x ( ) ( ) = , 那么函数 F x( ) 就称为 f x( ) 在区间 I 上的原函数. 2.原函数的性质 (1)原函数的存在性:连续函数一定存在原函数. (2)原函数是某个区间上的连续且可微的函数. (3) F x( ) 是 f x( ) 在某个区间上的一个原函数, 则 F x C ( ) + 也是 f x( ) 的原函数. 不定积分 几种特殊类型函数的积分 有理函数的积分 第二类换元法 换元积分法 分部积分法 不定积分的求法 原函数与不定积分的概念 三角有理函数的积分 简单无理函数的积分 基本性质 第一类换元法

(4)F(x)和Gx)均是f(x)在同一区间上的原函数,则F(x)和G(x)仅相差一个常数 约定在本章出现的C如果未加说明均指任意常数 注如果f)在区间1上连续,则fx)在区间1上存在原函数.反之,若fx)在区间 1内有原函数,了x)在区间1内却不一定连续,例如 F)sin 0x=0 在(一。,+∞)内处处有导数, 0 x=0 故f)在(-D,+o)内有原函数Fx),但f)显然在x=0处不连续.容易看出,这个间断 点是第二类间断点。所以,函数x)连续仅是存在原函数的充分条件而不是必要条件。 3.不定积分的定义 在区间1上,函数f(x)的带有任意常数项的原函数称为f(x)(或f(x)k)在区间I上 的不定积分,记作∫/x体.如果F(x)是fx)在区间I上的一个原函数,则 ∫fx)=Fx)+C, 或者称f(x)的原函数的全体为f(x)的不定积分. 4.积分与微分的关系 ①D/达]=或可/=达(先积后微,作用抵) (2)∫f(x)女=fx)+C或∫dx)=fx)+C.(先微后积,添加一个常数) 5.不定积分的性质 性质1设函数f)及g(x)的原函数存在,则 Jfx)±gxt=∫fxd±∫gx)达 性质2设函数x)的原函数存在,k为非零常数,则 ∫xd=kfx). (二)不定积分的积分方法 1.利用如下积分公式表 (1)∫=:+C(k是常数), 2jr+c(u-1 (3)∫=lnl+c (4)j=aanx+c, arcsin x+C (6)∫cos xdx=sinx+C
(4) F x( ) 和 G x( ) 均是 f x( ) 在同一区间上的原函数,则 F x( ) 和 G x( ) 仅相差一个常数. 约定 在本章出现的 C 如果未加说明均指任意常数. 注 如果 f x( ) 在区间 I 上连续,则 f x( ) 在区间 I 上存在原函数.反之,若 f x( ) 在区间 I 内有原函数, f x( ) 在区间 I 内却不一定连续.例如 2 1 sin , 0 ( ) , 0 0 x x F x x x = = , 在 (− + , ) 内处处有导数, 1 1 2 sin cos , 0 ( ) ( ) 0 0 x x F x f x x x x − = = = , 故 f x( ) 在 ( , ) − + 内有原函数 F x( ) ,但 f x( ) 显然在 x = 0 处不连续.容易看出,这个间断 点是第二类间断点.所以,函数 f x( ) 连续仅是存在原函数的充分条件而不是必要条件. 3.不定积分的定义 在区间 I 上,函数 f x( ) 的带有任意常数项的原函数称为 f x( ) (或 f x dx ( ) )在区间 I 上 的不定积分,记作 f x dx ( ) .如果 F x( ) 是 f x( ) 在区间 I 上的一个原函数,则 f x dx F x C ( ) ( ) = + , 或者称 f x( ) 的原函数的全体为 f x( ) 的不定积分. 4.积分与微分的关系 (1) ( ) ( ) d f x dx f x dx = 或 d f x dx f x dx [ ( ) ] ( ) = (先积后微,作用抵消) (2) f x dx f x C ( ) ( ) = + 或 df x f x C ( ) ( ) = + .(先微后积,添加一个常数) 5.不定积分的性质 性质 1 设函数 f x( ) 及 g x( ) 的原函数存在,则 [ ( ) ( )] ( ) ( ) f x g x dx f x dx g x dx = . 性质 2 设函数 f x( ) 的原函数存在, k 为非零常数,则 kf x dx k f x dx ( ) ( ) = . (二)不定积分的积分方法 1.利用如下积分公式表 (1) kdx kx C = + ( k 是常数), (2) 1 1 x x dx C + = + + ( −1 ), (3) ln dx x C x = + , (4) 2 arctan 1 dx x C x = + + , (5) 2 arcsin 1 dx x C x = + − , (6) cos sin xdx x C = +

(7)∫sinxdx=-cosx+C, (8)∫=jsec2d=tanx+C, (9)j产-joch=-mx+C, (10)[secxtanxdx=secx+C, (11)[cscxcotxdx =-cscx+C, (12)je=e+C, ajo=品c (14)∫shxdx=cdr+C (15)∫chxdx=shr+C (16)[tanxdx=-Incos+C (17)[cotxdx =Insin+C (18)[secxdx =Insecx+tanx+C (19)[cscxd=Incscx-cot+c (20》∫n中-rcan后+c awj产六c 2)j产am子c dx 23》∫a=l+F+)+c2∫。=nx+F-G+C d在 2.第一类换元法设f)具有原函数,M=)可导,则有换元公式 Jf几o(xlp'(x)t=[fu)dl-e· 这种方法又称为凑微分法,例如求积分「g(x),则要将g(x)凑成几(x()的形式, 而∫f(u)du容易积分,即∫f(u)du是属于公式表中有的类型或者接近的类型 3.第二类换元法设x=w)是单调的、可导的函数,并且w)≠0.又设几ww) 具有原函数,则有换元公式 这种方法是作新的代换,将∫x)本化成更容易积分的形式,常用的第二类换元法如三角代 换、倒代换等。 4.分部积分法若x)与(x)可导,且不定积分x(x存在,则不定积分 ∫x'x)也存在,并有 「mxr(xk=xrx)-「r'x(xk. 当被积函数是反三角函数、对数函数、幂函数、指数函数、三角函数(简称反、对、幂、指、 三)中的某两类函数的乘积时,通常用分部积分法。 5.有理函数的积分 (1)一般有理函数的积分:用待定系数法或赋值法将有理真分式化为部分分式之和
(7) sin cos xdx x C = − + , (8) 2 2 sec tan cos dx xdx x C x = = + , (9) 2 2 csc cot sin dx xdx x C x = = − + , (10) sec tan sec x xdx x C = + , (11) csc cot csc x xdx x C = − + , (12) x x e dx e C = + , (13) ln x x a a dx C a = + (14) shxdx chx C = + (15) chxdx shx C = + (16) tan ln cos xdx x C = − + (17) cot ln sin xdx x C = + (18) sec ln sec tan xdx x x C = + + (19) csc ln csc cot xdx x x C = − + (20) 2 2 1 arctan dx x C a x a a = + + (21) 2 2 1 ln 2 dx x a C x a a x a − = + − + (22) 2 2 arcsin dx x C a x a = + − (23) 2 2 2 2 ln( ) dx x x a C x a = + + + + (24) 2 2 2 2 ln( ) dx x x a C x a = + − + − 2.第一类换元法 设 f u( ) 具有原函数, u x =( ) 可导,则有换元公式 ( ) [ ( )] ( ) [ ( ) ] u x f x x dx f u du = = . 这种方法又称为凑微分法,例如求积分 g x dx ( ) ,则要将 g x( ) 凑成 f x x [ ( )] ( ) 的形式, 而 f u du ( ) 容易积分,即 f u du ( ) 是属于公式表中有的类型或者接近的类型. 3.第二类换元法 设 x t = ( ) 是单调的、可导的函数,并且 ( ) 0 t .又设 f t t [ ( )] ( ) 具有原函数,则有换元公式 1 ( ) ( ) [ [ ( )] ( ) ] t x f x dx f t t dt − = = . 这种方法是作新的代换,将 f x dx ( ) 化成更容易积分的形式,常用的第二类换元法如三角代 换、倒代换等. 4.分部积分法 若 u x( ) 与 v x( ) 可导,且不定积分 u x v x dx ( ) ( ) 存在,则不定积分 u x v x dx ( ) ( ) 也存在,并有 u x v x dx u x v x u x v x dx ( ) ( ) ( ) ( ) ( ) ( ) = − . 当被积函数是反三角函数、对数函数、幂函数、指数函数、三角函数(简称反、对、幂、指、 三)中的某两类函数的乘积时,通常用分部积分法. 5.有理函数的积分 (1)一般有理函数的积分:用待定系数法或赋值法将有理真分式化为部分分式之和

那么有理函数的积分就可转化为较简单的部分分式积分之和, (2)三角有理函数的积分:用万能公式将「R(sinx,cosx)k化为有理函数的积分. (3)其它简单无理函数的积分:通过适当变量代换使其转化为有理函数的积分
那么有理函数的积分就可转化为较简单的部分分式积分之和. (2)三角有理函数的积分:用万能公式将 R x x dx (sin ,cos ) 化为有理函数的积分. (3)其它简单无理函数的积分:通过适当变量代换使其转化为有理函数的积分.