
第四章不定积分 数学实验 利用Matlab软件中的函数int可以对不定积分进行符号计算,其调用格式和功能如下 所示 int(s) 求符号表达式s的不定积分 int(s,x) 求符号表达式s关于变量x的不定积分 说明:在初等函数范围内,不定积分有时是不存在的,也就是说,即使(x)是初等函数 但是不定积分∫/xd却不一定是初等函数例如,e,nx,C, 吧是初等数, 面小e血,了受4,配每不能用初等西数表示出来比如,给入程序: 1 >》5ymsX >F=int(sin(x)/x) 运行后屏幕显示: F =sinint(x) 其中sinint(x)是非初等函数,称作积分正弦函数.在使用int函数求不定积分时,读者要注 意这种情况. 例1求∫x2 sinxdx 解用符号积分命令int计算此积分,Matlab程序为 >syms x: >int(x"2*sin(x)) 结果为an5=-x^2*cos(x)+2*cos(x)+2*x*sin(x) 如果用微分命令diff验证积分正确性,Matlab程序为 >diff(-x"2*cos(x)+2*cos(x)+2*x*sin(x)) 结果为 ans =x'2*sin(x) 例2求下列函数的一个原函数: (1)x: (2)e (e-amx:(3)1+cos2x (4)nr+) 2x+3 x+l' (5)x2 arctanx (6)7+3x-10 解(1)相应的Matlab程序为 >clear all:
1 第四章 不定积分 数学实验 利用 Matlab 软件中的函数 int 可以对不定积分进行符号计算,其调用格式和功能如下 所示. int(s) int(s,x) 求符号表达式 s 的不定积分 求符号表达式 s 关于变量 x 的不定积分 说明:在初等函数范围内,不定积分有时是不存在的,也就是说,即使 f x( ) 是初等函数, 但是不定积分 f x x ( )d 却不一定是初等函数.例如, 2 e −x , sin x x , e x x , 1 loga x 是初等函数, 而 2 e dx x − , sin d x x x , e d x x x , 1 d loga x x 却不能用初等函数表示出来.比如,输入程序: >> syms x >> F=int(sin(x)/x) 运行后屏幕显示: F =sinint(x) 其中 sinint(x)是非初等函数,称作积分正弦函数.在使用 int 函数求不定积分时,读者要注 意这种情况. 例 1 求 2 x x x sin d . 解 用符号积分命令 int 计算此积分,Matlab 程序为 >> syms x; >> int(x^2*sin(x)) 结果为 ans =-x^2*cos(x)+2*cos(x)+2*x*sin(x) 如果用微分命令 diff 验证积分正确性,Matlab 程序为 >> diff(-x^2*cos(x)+2*cos(x)+2*x*sin(x)) 结果为 ans =x^2*sin(x) 例 2 求下列函数的一个原函数: (1) x x ; (2) sec (sec tan ) x x x − ; (3) 1 1 cos 2 + x ; (4) ln( 1) 1 x x + + ; (5) 2 x x arctan ; (6) 2 2 3 3 10 x x x + + − 解(1)相应的 Matlab 程序为 >> clear all;

>syms x: >f=x*sart (x) >int(f,x) 结果为ans=2/5*x(5/2): (2)相应的Matlab程序为 >clear all >》syms x >f=sec(x)*(sec(x)-tan(x)): >int(f.x) 结果为ans=sin(x)/cos(x)-1/cos(x): (3)相应的Matlab程序为 >clear all >syms x: >f=1/(1+cos(2*x): >int(f.x) 结果为ans=1/2*tan(x): (4)相应的Matlab程序为 >clear all >SVms x: >f=log(x+1)/sqrt(x+1): >int (f.x) 结果为ans=2*1og(x+1)*(x+1)(1/2)-4*(x+1)(1/2): (5)相应的Matlab程序为 >>clear all >svms x: >》f=x^2*atan(x): >int (f,x) 结果为ans=1/3*x^3*atan(x)-1/6*x^2+1/6*1og(x^2+1): (6)相应的Matlab程序为 >>clear all >syms x: >f=(2*x+3)/(x^2+3*x-10): >int (f,x) 结果为ans=1og(x^2+3*x-10). 例3设曲线通过点(L,2),且其切线的斜率为3x2+2x-9,求此曲线的方程并绘制其图像 解设所求的曲线方程为y=f),根据题意,y=3x2+2x-9,所以 y=∫y'r=∫3xr2+2x-9d 相应的Matlab程序为 >syms x C: >》f=3*x^2+2*x-9:
2 >> syms x; >> f=x*sqrt(x); >> int(f,x) 结果为 ans =2/5*x^(5/2); (2)相应的 Matlab 程序为 >> clear all >> syms x; >> f=sec(x)*(sec(x)-tan(x)); >> int(f,x) 结果为 ans =sin(x)/cos(x)-1/cos(x); (3)相应的 Matlab 程序为 >> clear all >> syms x; >> f=1/(1+cos(2*x)); >> int(f,x) 结果为 ans =1/2*tan(x); (4)相应的 Matlab 程序为 >> clear all >> syms x; >> f=log(x+1)/sqrt(x+1); >> int(f,x) 结果为 ans =2*log(x+1)*(x+1)^(1/2)-4*(x+1)^(1/2); (5)相应的 Matlab 程序为 >> clear all >> syms x; >> f=x^2*atan(x); >> int(f,x) 结果为 ans =1/3*x^3*atan(x)-1/6*x^2+1/6*log(x^2+1); (6)相应的 Matlab 程序为 >> clear all >> syms x; >> f=(2*x+3)/(x^2+3*x-10); >> int(f,x) 结果为 ans =log(x^2+3*x-10). 例 3 设曲线通过点 (1,2) ,且其切线的斜率为 2 3 2 9 x x + − ,求此曲线的方程并绘制其图像. 解 设所求的曲线方程为 y f x = ( ) ,根据题意, 2 y x x = + − 3 2 9 ,所以 2 y y x x x x = = + − d (3 2 9)d 相应的 Matlab 程序为 >> syms x C; >> f=3*x^2+2*x-9;
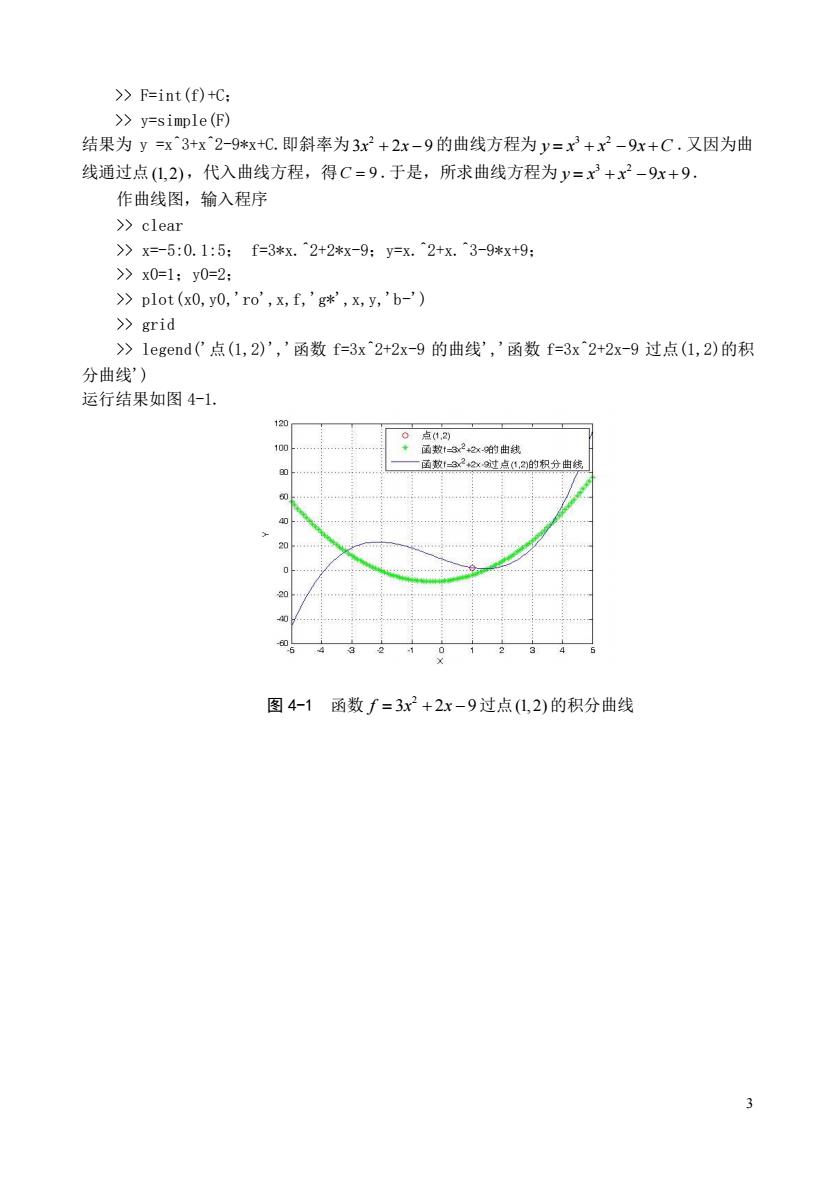
>F=int(f)+C: >y=simple(F) 结果为y=x^3+x^2-9*x+C.即斜率为3x2+2r-9的曲线方程为y=x2+xX2-9x+C.又因为曲 线通过点(L,2),代入曲线方程,得C=9.于是,所求曲线方程为y=x+x2-9x+9 作曲线图,给入程序 >>clear >》X=-5:0.1:5:f=3*x.^2+2*x-9:y=x.2+x.^3-9*x+9: >》x0=1:y0=2: >plot(x0,y0,'ro',x,f,'g*',x,y,'b-') >grid >1 egend('点(1,2)',’函数f=3x^2+2x9的曲线',’函数f=3x2+2x-9过点(1,2)的积 分曲线) 运行结果如图4-1. 的由线 2过点L2的分由 21 图4-1函数f=3x2+2x-9过点(L,2)的积分曲线 3
3 >> F=int(f)+C; >> y=simple(F) 结果为 y =x^3+x^2-9*x+C.即斜率为 2 3 2 9 x x + − 的曲线方程为 3 2 y x x x C = + − + 9 .又因为曲 线通过点 (1,2) ,代入曲线方程,得 C = 9 .于是,所求曲线方程为 3 2 y x x x = + − + 9 9 . 作曲线图,输入程序 >> clear >> x=-5:0.1:5; f=3*x.^2+2*x-9;y=x.^2+x.^3-9*x+9; >> x0=1;y0=2; >> plot(x0,y0,'ro',x,f,'g*',x,y,'b-') >> grid >> legend('点(1,2)','函数 f=3x^2+2x-9 的曲线','函数 f=3x^2+2x-9 过点(1,2)的积 分曲线') 运行结果如图 4-1. 图 4-1 函数 2 f x x = + − 3 2 9 过点 (1,2) 的积分曲线