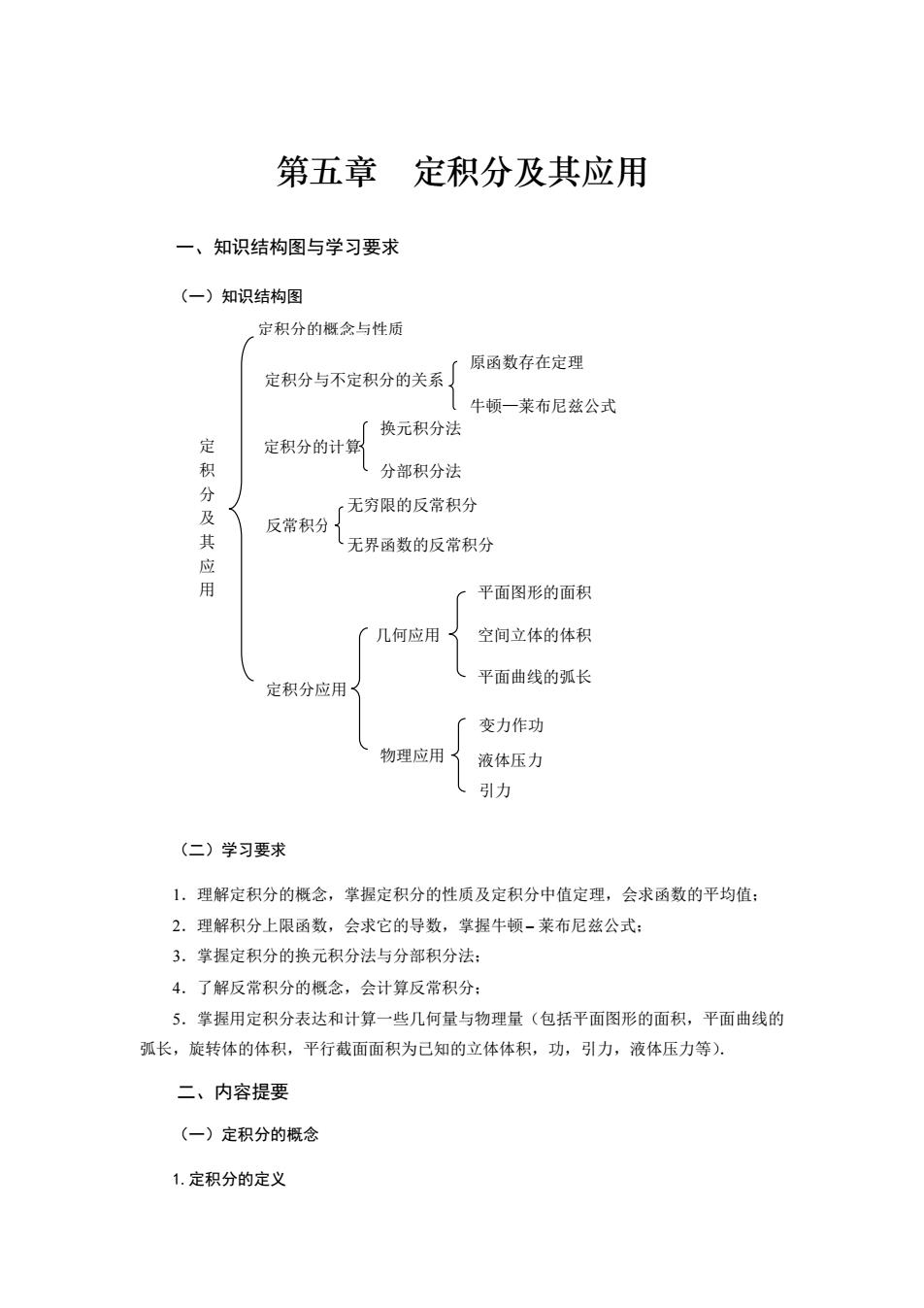
第五章定积分及其应用 一、知识结构图与学习要求 (一)知识结构图 ,定积分的概今与性质 原函数存在定理 定积分与不定积分的关系」 【牛顿一莱布尼兹公式 换元积分 定 定积分的计算 、分部积分法 无穷限的反常积分 反常积分 (无界函数的反常积分 多 平面图形的面积 千几何应用〈 空间立体的体积 定积分应用 (平面曲线的弧长 「变力作功 物理应用〈 液体压力 (引力 (二)学习要求 1.理解定积分的概念,掌握定积分的性质及定积分中值定理,会求函数的平均值 2.理解积分上限函数,会求它的导数,掌握牛顿-莱布尼兹公式: 3.掌握定积分的换元积分法与分部积分法: 4.了解反常积分的概念,会计算反常积分: 5.掌据用定积分表达和计算一些几何量与物理量(包括平面图形的面积,平面曲线的 弧长,旋转体的体积,平行截面面积为已知的立体体积,功,引力,液体压力等). 二、内容提要 (一)定积分的概念 1.定积分的定义
第五章 定积分及其应用 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解定积分的概念,掌握定积分的性质及定积分中值定理,会求函数的平均值; 2.理解积分上限函数,会求它的导数,掌握牛顿 − 莱布尼兹公式; 3.掌握定积分的换元积分法与分部积分法; 4.了解反常积分的概念,会计算反常积分; 5.掌握用定积分表达和计算一些几何量与物理量(包括平面图形的面积,平面曲线的 弧长,旋转体的体积,平行截面面积为已知的立体体积,功,引力,液体压力等). 二、内容提要 (一)定积分的概念 1.定积分的定义 定 积 分 及 其 应 用 定积分应用 平面图形的面积 原函数存在定理 反常积分 牛顿—莱布尼兹公式 定积分与不定积分的关系 定积分的概念与性质 空间立体的体积 平面曲线的弧长 定积分的计算 几何应用 无界函数的反常积分 无穷限的反常积分 物理应用 变力作功 换元积分法 引力 液体压力 分部积分法

定积分是积分和的极限,即 ∫广fx)t=lim∑f(5)Ax 定积分的值完全由被积函数和积分区间所确定,而与积分变量的记法无关。 2.定积分的几何意义 表示介于曲线y=fx)、x轴、直线x=a及x=b各部分面积的代数和 3.定积分的可积性 (1)有限区间上的连续函数一定可积: (2)有限区间上有界且只有有限多个间断点的函数也可积 (二)定积分的性质 L.规定fxd=0,fx=∫fx 2.∫[fx)±gxt=∫fx±gxt: 3.∫x)本=fx达(k是常数) 4.1.dx=b-a; 5.∫fx=fxd+fxd: 6.若fx)≥0,则fx20(a<b): 7.若fx)≥gx),则∫fx)t≥gxt(a<b: 8.(x)d(xd (a<b): 9.若msf)sM,x∈[a,b,则 mb-a)sfxt≤Mb-a): 10.定积分中值定理设函数fx)在闭区间[a,b]上连续,则在积分区间[a,上至少存 在一点5使得 ["f(x)dx=f(EXb-a): 11.定积分中值定理的推广设函数f(x)在闭区间[a,上连续,函数g(x)不变号,则 在[a,b)上至少存在一点E使得 [f(x)g(x)d=f()g(x)dx. (三)积分上限函数及其导数 1.定义
定积分是积分和的极限,即 0 1 ( ) lim ( ) n b i i a i f x dx f x → = = 定积分的值完全由被积函数和积分区间所确定, 而与积分变量的记法无关. 2.定积分的几何意义 表示介于曲线 y f x = ( ) 、 x 轴、直线 x a = 及 x b = 各部分面积的代数和. 3.定积分的可积性 (1)有限区间上的连续函数一定可积; (2)有限区间上有界且只有有限多个间断点的函数也可积. (二)定积分的性质 1.规定 ( ) 0 a a f x dx = , ( ) ( ) b a a b f x dx f x dx = − ; 2. [ ( ) ( )] ( ) ( ) b b b a a a f x g x dx f x dx g x dx = ; 3. ( ) ( ) b b a a kf x dx k f x dx = ( k 是常数); 4. 1 b a = − dx b a ; 5. ( ) ( ) ( ) b c b a a c f x dx f x dx f x dx = + ; 6. 若 f x( ) 0 ,则 ( ) 0 ( ) b a f x dx a b ; 7. 若 f x g x ( ) ( ) ,则 ( ) ( ) ( ) b b a a f x dx g x dx a b ; 8. ( ) ( ) ( ) b b a a f x dx f x dx a b ; 9. 若 m f x M ( ) , x a b [ , ] , 则 ( ) ( ) ( ) b a m b a f x dx M b a − − ; 10. 定积分中值定理 设函数 f x( ) 在闭区间 [ , ] a b 上连续,则在积分区间 [ , ] a b 上至少存 在一点 使得 ( ) ( )( ) b a f x dx f b a = − ; 11. 定积分中值定理的推广 设函数 f x( ) 在闭区间 [ , ] a b 上连续,函数 g x( ) 不变号,则 在 [ , ] a b 上至少存在一点 使得 ( ) ( ) ( ) ( ) b b a a f x g x dx f g x dx = . (三)积分上限函数及其导数 1.定义

设函数fx)在闭区间[a,b上连续,称)=广f0h为积分上限函数,其中x∈a,: 完全类似地可定义积分下限函数 2.原函数存在定理 如果函数fx)在区间[a,上连续,则积分上限函数(x)=了广f)h在[a,b)上可导,其 导数为 )=&f0h=)(asxsb创 推论1(x)是fx)在[a,b1上的一个原函数,即连续函数的原函数一定存在. 推论2设∫为连续函数,u与v均为可导函数,且复合函数几u(x儿,f(x川都存在, 则有 &foh=ee)-us咖e 注上述公式条件是被积函数f0连续且被积表达式fd中不含有变量x。 (四)定积分的计算 1.牛顿-莱布尼兹公式 设F(x)是连续函数fx)在区间[a,)上的一个原函数,则有 ∫fx)d=Fb)-Fa, 此公式又称微积分基本公式. 2.定积分的换元积分法 设fx)在区间[a,月上连续,p)在[a,B例或[B,a]上连续,则 ∫fx=几op'u)dh 其中a=a,b=B) 注使用定积分的换元法时,应注意两点:一是所设的变量代换在定义区间上要具有连 续导数:二是该变量代换要为单调函数 3.定积分的分部积分法 设u=x),v=x)有连续导数,则 [广uh=[mt-∫"th 4.对于一些特殊类型的积分,有如下常用结论: (1)若fx)在[-a,ad上连续且f(x)为偶函数,则 f(x)d=2[f(x)dx (2)若fx)在-a,d上连续且fx)为奇函数,则 fx)=0:
设函数 f x( ) 在闭区间 [ , ] a b 上连续,称 ( ) ( ) x a = x f t dt 为积分上限函数,其中 x a b [ , ] ; 完全类似地可定义积分下限函数. 2.原函数存在定理 如果函数 f x( ) 在区间 [ , ] a b 上连续, 则积分上限函数 ( ) ( ) x a = x f t dt 在 [ , ] a b 上可导,其 导数为 ( ) ( ) ( ) x a d x f t dt f x dx = = ( ) a x b . 推论 1 ( ) x 是 f x( ) 在 [ , ] a b 上的一个原函数,即连续函数的原函数一定存在. 推论 2 设 f 为连续函数, u 与 v 均为可导函数,且复合函数 f u x f v x [ ( )], [ ( )] 都存在, 则有 ( ) ( ) ( ) [ ( )] ( ) [ ( )] ( ) v x u x d f t dt f v x v x f u x u x dx = − . 注 上述公式条件是被积函数 f t() 连续且被积表达式 f t dt ( ) 中不含有变量 x . (四)定积分的计算 1.牛顿 − 莱布尼兹公式 设 F x( ) 是连续函数 f x( ) 在区间 [ , ] a b 上的一个原函数,则有 ( ) ( ) ( ) b a f x dx F b F a = − , 此公式又称微积分基本公式. 2.定积分的换元积分法 设 f x( ) 在区间 [ , ] a b 上连续, ()t 在 [ , ] 或 [ , ] 上连续,则 ( ) [ ( )] ( ) b a f x dx f t t dt = , 其中 a b = = ( ), ( ). 注 使用定积分的换元法时,应注意两点:一是所设的变量代换在定义区间上要具有连 续导数;二是该变量代换要为单调函数. 3.定积分的分部积分法 设 u u x v v x = = ( ), ( ) 有连续导数, 则 [ ] b b b a a a udv uv vdu = − . 4.对于一些特殊类型的积分,有如下常用结论: (1)若 f x( ) 在 [ , ] −a a 上连续且 f x( ) 为偶函数,则 0 ( ) 2 ( ) a a a f x dx f x dx − = ; (2)若 f x( ) 在 [ , ] −a a 上连续且 f x( ) 为奇函数,则 ( ) 0 a a f x dx − = ;

(3)若fx)是以T为周期的连续函数,则 ∫fx=nfxd=nfxd 其中a是任意常数,n为整数: (4)若x)在0,上连续,则有 信fsn达-f(cosxybs, f(sinx)d=2f(sinx)d, (sin)d(sin)ds. (6)cos=后sim'= 只号2ueN 只器 n=2k,keN (五)反常积分 1.无穷限的反常积分 设函数x)在相应区间上连续,定义 fx)d=imJ广fx)d:八fx)d=lim f()d 若上述等式右端极限存在,则称左边的反常积分收敛,否则称为发散 而 fx)=fx)本+心fx达 当广fx达和心fx)达同时收敛时,称反常积分广fx达收敛,否则称为发散。 2.无界函数的反常积分(瑕积分) 设函数x)在相应区间上连续,且分别在a的右邻域、b的左邻域、c的邻域内无界, 定义:fx=limf():∫fx)=limf( 若上述等式右端极限存在,则称左边的反常积分收敛,否则称为发散 而 ∫fxd=∫fxd+f 当x)达和广fx)同时收敛时,称反常积分fx达收敛,否则称为发散. (六)定积分的应用 1.运用元素法建立所求量的定积分表达式的一般步骤: (1)根据问题的具体情形,选取一个变量(如x)作为积分变量,并确定该积分变量的 变化区间[ab1: (2)任取一小区间记为[x,x+],计算出在此小区间上的部分量AU的近似值:
(3)若 f x( ) 是以 T 为周期的连续函数,则 0 ( ) ( ) ( ) a nT a T T a a f x dx n f x dx n f x dx + + = = , 其中 a 是任意常数, n 为整数; (4)若 f x( ) 在 [0,1] 上连续,则有 2 0 f x dx (sin ) = 2 0 f x dx (cos ) , 0 f x dx (sin ) = 2 0 2 (sin ) f x dx , 0 xf x dx (sin ) = 0 (sin ) 2 f x dx . (5) 2 2 0 0 cos sin n n xdx xdx = = 1 3 4 2 , 2 1, 2 5 3 1 3 1 , 2 , 2 2 2 n n n k k N n n n n n k k N n n − − = + − − − = − . (五)反常积分 1. 无穷限的反常积分 设函数 f x( ) 在相应区间上连续,定义 ( ) lim ( ) b a a b f x dx f x dx + →+ = ; ( ) lim ( ) b b a a f x dx f x dx − →− = 若上述等式右端极限存在,则称左边的反常积分收敛,否则称为发散. 而 0 0 f x dx f x dx f x dx ( ) ( ) ( ) + + − − = + 当 0 f x dx ( ) + 和 0 f x dx ( ) − 同时收敛时, 称反常积分 f x dx ( ) + − 收敛,否则称为发散. 2.无界函数的反常积分(瑕积分) 设函数 f x( ) 在相应区间上连续,且分别在 a 的右邻域、 b 的左邻域、 c 的邻域内无界, 定义: ( ) lim ( ) b b a t t a f x dx f x dx → + = ; ( ) lim ( ) b t a a t b f x dx f x dx → − = 若上述等式右端极限存在,则称左边的反常积分收敛,否则称为发散. 而 ( ) ( ) ( ) b c b a a c f x dx f x dx f x dx = + 当 ( ) c a f x dx 和 ( ) b c f x dx 同时收敛时, 称反常积分 ( ) b a f x dx 收敛,否则称为发散. (六)定积分的应用 1.运用元素法建立所求量的定积分表达式的一般步骤: (1)根据问题的具体情形,选取一个变量(如 x )作为积分变量,并确定该积分变量的 变化区间 [ , ] a b ; (2)任取一小区间记为 [ , ] x x dx + ,计算出在此小区间上的部分量 U 的近似值:

dU=fx)本,称它是所求量U的元素: (3)以fx女作为被积表达式,在区间[a,b上作定积分,即U=[fx) 2.求平面图形的面积 (1)直角坐标系的情形: 由连续曲线y=fx),(∫x)≥0),直线x=a,x=b及x轴所围成的曲边梯形的面积 A=f(x)ds (a<b): (2)参数方程情形: 由连续曲线x=9),y=)(a≤1sB),直线x=a,x=b及x轴所围成的曲边梯形的 面积 A=v((dt: (3)极坐标情形: 连续曲线p=(8)以及0=a,0=B(a≤B)所围成的图形的面积 A=te(OF do 3.立体的体积 (1)旋转体的体积 由连续曲线y=∫x),直线x=a,x=b及x轴所围成的曲边梯形绕x轴旋转一周的旋 转体的体积为 V=πfx(a<b): 当a≥0,f(x)≥0时,此曲边梯形绕y轴旋转一周的旋转体的体积为 ,=2πfxd (2)平行截面面积为已知的立体的体积 设连续函数x)表示过点x且垂直于x轴的截面面积,则该立体的体积为 V=4x达 4.平面曲线的弧长 (1)直角坐标系的情形 y=f(x)(asxsb),ds=+f(xd,s=[+(xx (2)参数方程情形 x=).y=w()(astsB),ds=+dr,s=[+di (3)极坐标情形 r=r(0)(asosB),ds=r(+r(o de,s=[r(+r(o)de
dU f x dx = ( ) ,称它是所求量 U 的元素; (3)以 f x dx ( ) 作为被积表达式,在区间 [ , ] a b 上作定积分,即 ( ) b a U f x dx = . 2.求平面图形的面积 (1)直角坐标系的情形: 由连续曲线 y f x = ( ) ,( f x( ) 0 ),直线 x a = , x b = 及 x 轴所围成的曲边梯形的面积 ( ) ( ) b a A f x dx a b = ; (2)参数方程情形: 由连续曲线 x t y t t = = ( ), ( ) ( ) ,直线 x a = ,x b = 及 x 轴所围成的曲边梯形的 面积 A t t dt ( ) ( ) = ; (3)极坐标情形: 连续曲线 = ( ) 以及 = = , ( )所围成的图形的面积 1 2 [ ( )] 2 A d = . 3.立体的体积 (1)旋转体的体积 由连续曲线 y f x = ( ) ,直线 x a = , x b = 及 x 轴所围成的曲边梯形绕 x 轴旋转一周的旋 转体的体积为 2 [ ( )] ( ) b x a V f x dx a b = ; 当 a f x 0, ( ) 0 时,此曲边梯形绕 y 轴旋转一周的旋转体的体积为 2 ( ) b y a V xf x dx = . (2)平行截面面积为已知的立体的体积 设连续函数 A x( ) 表示过点 x 且垂直于 x 轴的截面面积,则该立体的体积为 ( ) b a V A x dx = . 4. 平面曲线的弧长 (1)直角坐标系的情形 y f x a x b = ( ) ( ) , 2 ds f x dx = +1 [ ( )] , 2 1 [ ( )] b a s f x dx = + ; (2)参数方程情形 x t y t t = = ( ), ( ) ( ) , 2 2 ds t t dt = + [ ( )] [ ( )] , 2 2 s t t dt [ ( )] [ ( )] = + ; (3)极坐标情形 r r = ( ) ( ) , 2 2 ds r r d = + [ ( )] [ ( )] , 2 2 s r r d [ ( )] [ ( )] = + .

5.变力沿直线所作的功 物体在平行于x轴的力F(x)作用下由x=a处运动到x=b处,力F(x)所作的功为 w-F(ds. 6.水压力 设一薄板铅直浸在相对密度为y的静止液体中,薄板上、下与液面平行且分别位于 x=a,x=b处(原点在液面上),两腰分别为y=fx).y=g(x),则薄板一侧所受压力为 P=∫yxx)-gx 7.引力 主要利用万有引力公式
5.变力沿直线所作的功 物体在平行于 x 轴的力 F x( ) 作用下由 x a = 处运动到 x b = 处,力 F x( ) 所作的功为 ( ) b a W F x dx = . 6.水压力 设一薄板铅直浸在相对密度为 的静止液体中,薄板上、下与液面平行且分别位于 x a = , x b = 处(原点在液面上),两腰分别为 y f x y g x = = ( ), ( ) ,则薄板一侧所受压力为 ( ) ( ) b a P x f x g x dx = − . 7.引力 主要利用万有引力公式.