
第一章 函数与极限 数学实验 一、一元函数作图(二维图形) 函数的图形不仅揭示了函数的本质特性,有时还是解题的钥匙.例如,观察函数 )=xmx的图形可知当x→0时,f)=xsmx是无穷小:根据函数f)=sn的图形可 以判定x=0为函数的振荡间断点等. Matlab软件为我们提供了众多的功能强大的图形绘制函数.plot是Matlab中最常用的 画平面曲线的函数,它的主要功能是用于绘制显示函数y=x)和参数式函数x=x), y=)的平面曲线.plot函数的调用格式如下: PIot(x,y,'可选项s') 其中x是曲线上的横坐标,y是曲线上的纵坐标,'可选项s'中通常包含确定曲线颜色、 线型、两坐标轴上的比例等等参数.在作图时可根据需要选择可选项,如果在绘图时省略可 选项,那么Dlot函数将自动选择一组默认值,画出曲线, ezplot是Matlab中另外一个画平面曲线的函数,它的主要功能是用于绘制隐函数 F(x,y)=0、参数式函数x=x(),y=)和显示函数y=f(x)的平面曲线.ezplot函数的调 用格式如下: ezplot(F,[a,b,c,d)绘制隐函数F(,y)=0在a≤x≤b和c≤y≤d上的平面曲线. ezplot(F,[a,b]) 绘制隐函数F(x,)=0在a≤x≤b和a≤y≤b上的平面曲线 ezplot(x,y,[a,b])绘制参数方程x=x(),y=)在a≤t≤b上的平面曲线. polar的主要功能是用于绘制极坐标函数p=p(0)的平面曲线,它的调用格式如下: polar (THETA,RHO,'s') 其中THETA是极角(弧度值),RHO是极径,s是可选项,s的内容和用法与前面的plot函数 完全相同. 例1作函数y=sinx,,y=cosx的图形,并观察它们的周期性 解先作函数y=sinx在[-4元,4π上的图形,用Matlab作图的程序为 >>x=linspace(-4*pi,4*pi,300): %产生300维向量x >>y=sin(x): >plot(x,y) %二维图形绘图命令 运行结果如图1-35.上述语句中,%后面如“%二维图形绘图命令”是说明性语句,无需键入
1 第一章 函数与极限 数学实验 一、一元函数作图(二维图形) 函数的图形不仅揭示了函数的本质特性,有时还是解题的钥匙.例如,观察函数 f x x x ( ) sin = 的图形可知当 x →0 时, f x x x ( ) sin = 是无穷小;根据函数 1 f x( ) sin x = 的图形可 以判定 x = 0 为函数的振荡间断点等. Matlab 软件为我们提供了众多的功能强大的图形绘制函数.plot 是 Matlab 中最常用的 画平面曲线的函数,它的主要功能是用于绘制显示函数 y f x = ( ) 和参数式函数 x x t = ( ) , y y t = ( ) 的平面曲线.plot 函数的调用格式如下: Plot(x,y,′可选项 s′) 其中 x 是曲线上的横坐标,y 是曲线上的纵坐标,′可选项 s′中通常包含确定曲线颜色、 线型、两坐标轴上的比例等等参数.在作图时可根据需要选择可选项,如果在绘图时省略可 选项,那么 plot 函数将自动选择一组默认值,画出曲线. ezplot 是 Matlab 中另外一个画平面曲线的函数,它的主要功能是用于绘制隐函数 F x y ( , ) 0 = 、参数式函数 x x t = ( ) ,y y t = ( ) 和显示函数 y f x = ( ) 的平面曲线.ezplot 函数的调 用格式如下: ezplot(F,[a,b,c,d]) 绘制隐函数 F x y ( , ) 0 = 在 a ≤ x ≤ b 和 c ≤ y ≤ d 上的平面曲线. ezplot(F,[a,b]) 绘制隐函数 F x y ( , ) 0 = 在 a ≤ x ≤ b 和 a ≤ y ≤ b 上的平面曲线. ezplot(x,y,[a,b]) 绘制参数方程 x x t = ( ) , y y t = ( ) 在 a ≤ t ≤ b 上的平面曲线. polar 的主要功能是用于绘制极坐标函数 = ( ) 的平面曲线,它的调用格式如下: polar(THETA,RHO,′s′) 其中 THETA 是极角(弧度值),RHO 是极径,s 是可选项,s 的内容和用法与前面的 plot 函数 完全相同. 例 1 作函数 y x = sin , y x = cos 的图形,并观察它们的周期性. 解 先作函数 y x = sin 在 [ 4 ,4 ] − 上的图形,用 Matlab 作图的程序为 >>x=linspace(-4*pi,4*pi,300); %产生 300 维向量 x >>y=sin(x) ; >>plot(x,y) %二维图形绘图命令 运行结果如图 1-35.上述语句中,%后面如“%二维图形绘图命令”是说明性语句,无需键入
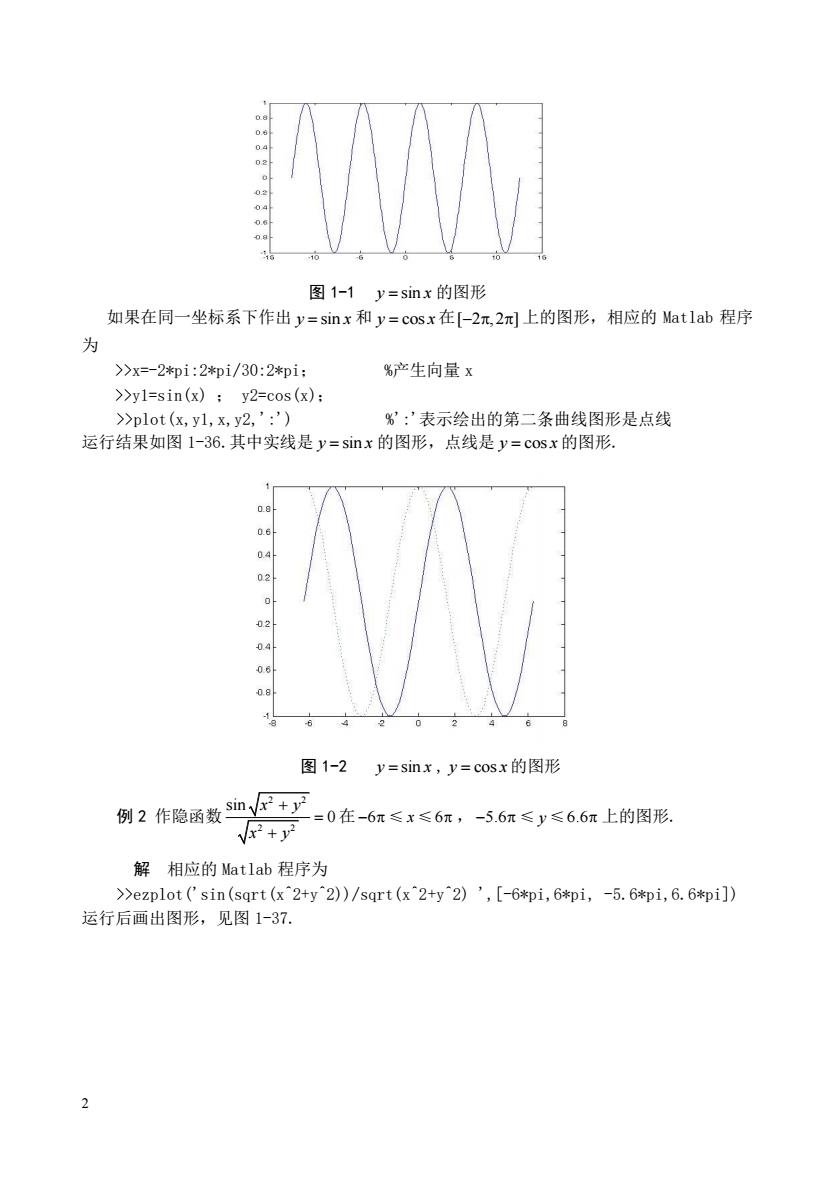
图1-1y=sinx的图形 如果在同一坐标系下作出y=sinx和y=cosx在[-2元2上的图形,相应的Matlab程序 为 >x=-2*pi:2*和i/30:2*和i: %产生向量x >>yl=sin(x):y2=cos(x); 2plot6xy1,x,y2,' %:'表示绘出的第二条曲线图形是点线 运行结果如图1-36.其中实线是y=sinx的图形,点线是y=cosx的图形. 0 图1-2 y=sinx,y=cosx的图形 例2作隐函数血F+户 =0在-6π≤x≤6m,-5.6π≤y≤6.6π上的图形 x2+y2 解相应的Matlab程序为 >>ezplot ('sin(sqrt (x"2+y"2))/sqrt(x"2+y"2)'[-6*pi,6*pi,-5.6*pi,6.6*pi]) 运行后画出图形,见图1-37
2 图 1-1 y x = sin 的图形 如果在同一坐标系下作出 y x = sin 和 y x = cos 在 [ 2 ,2 ] − 上的图形,相应的 Matlab 程序 为 >>x=-2*pi:2*pi/30:2*pi; %产生向量 x >>y1=sin(x) ; y2=cos(x); >>plot(x,y1,x,y2,':') %':'表示绘出的第二条曲线图形是点线 运行结果如图 1-36.其中实线是 y x = sin 的图形,点线是 y x = cos 的图形. 图 1-2 y x = sin , y x = cos 的图形 例 2 作隐函数 2 2 2 2 sin 0 x y x y + = + 在 − 6 ≤ x ≤ 6 , − 5.6 ≤ y ≤ 6.6 上的图形. 解 相应的 Matlab 程序为 >>ezplot('sin(sqrt(x^2+y^2))/sqrt(x^2+y^2) ',[-6*pi,6*pi, -5.6*pi,6.6*pi]) 运行后画出图形,见图 1-37
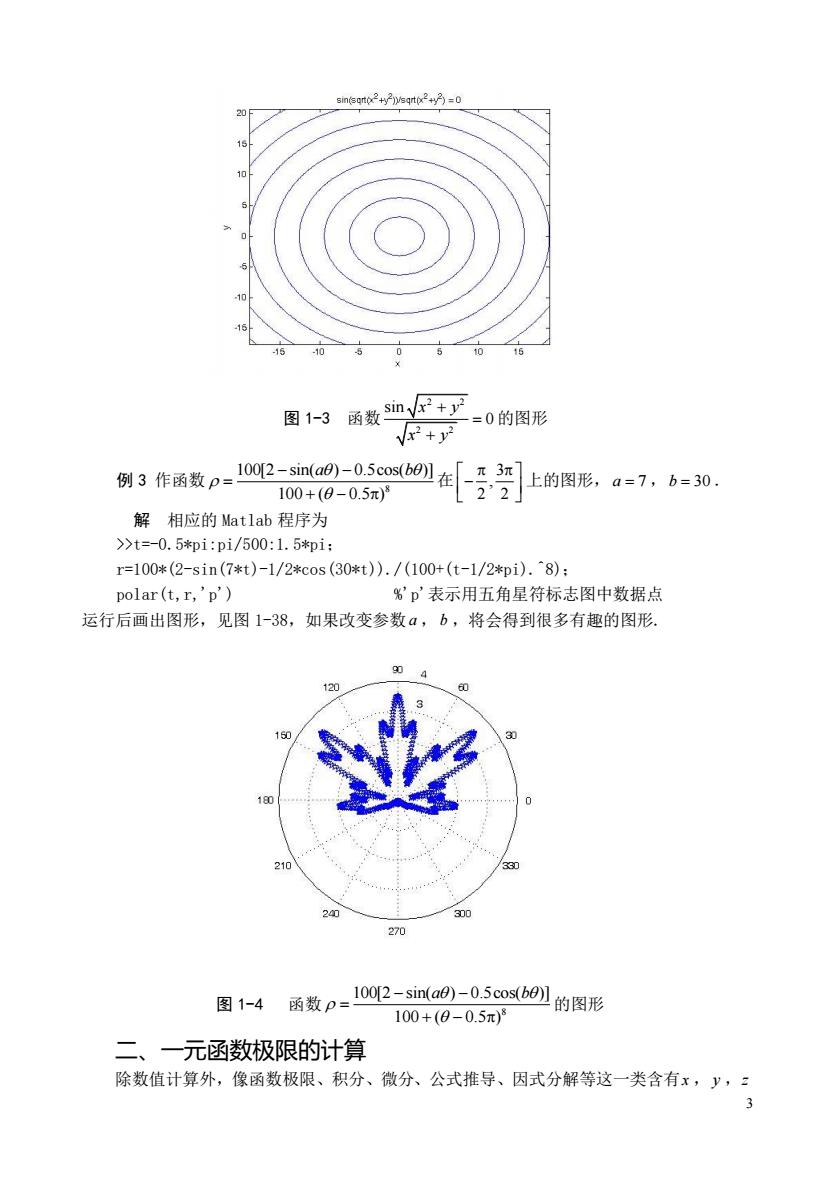
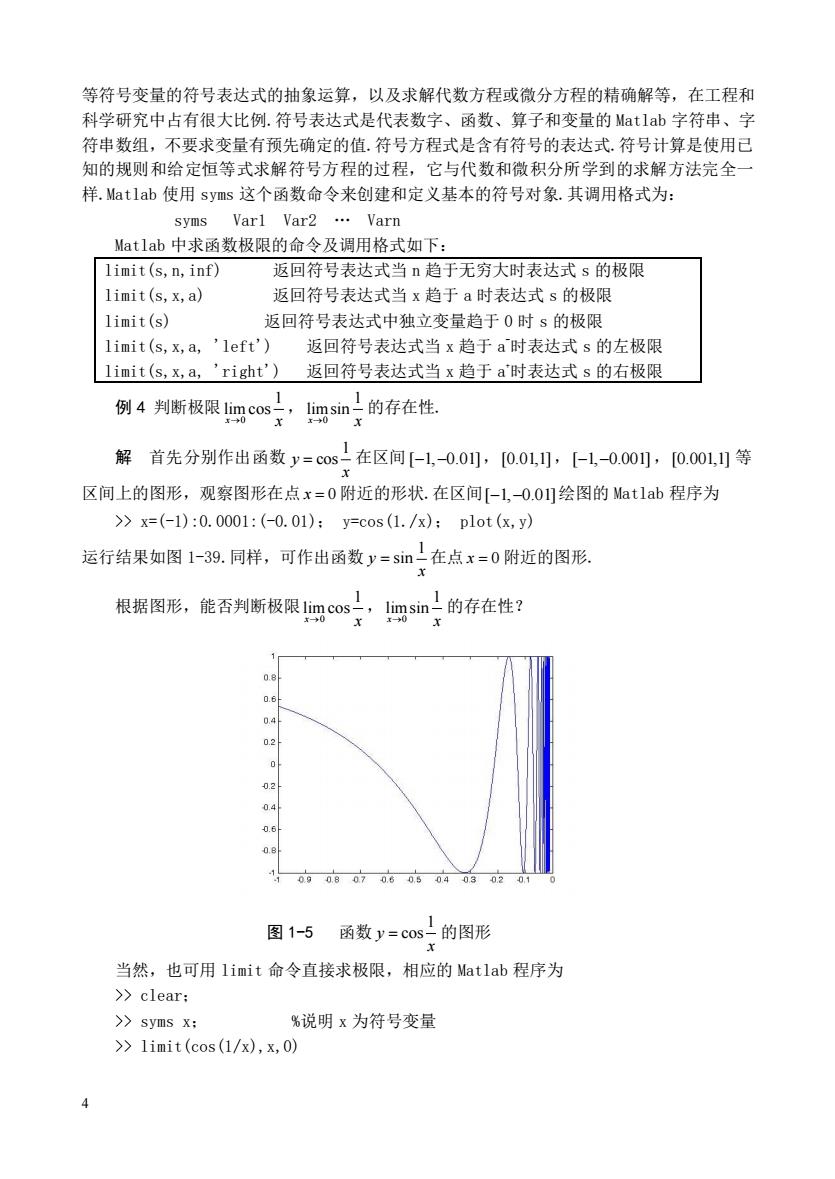
ane9o2+gtw2-0 图13函数咖P+ ·=0的图形 r+y 例3作西数p-10@P:@0g在[]上的图形,a=7,6=0 100+(8-0.5m) 解相应的latlab程序为 >t=-0.5*pi:pi/500:1.5*i: r=100*(2-sin(7*t)-1/2*cos(30*t)./(100+(t-1/2*pi).8): polar(t,r,'p') %p'表示用五角星符标志图中数据点 运行后画出图形,见图1-38,如果改变参数a,b,将会得到很多有趣的图形 0 120 27 图1-4 函数p=102-sm-05cosb0的图形 100+(0-0.5π) 二、一元函数极限的计算 除数值计算外,像函数极限、积分、微分、公式推导、因式分解等这一类含有x,y,: 3
3 图 1-3 函数 2 2 2 2 sin 0 x y x y + = + 的图形 例 3 作函数 8 100[2 sin( ) 0.5cos( )] 100 ( 0.5 ) a b − − = + − 在 3 , 2 2 − 上的图形, a = 7 ,b = 30 . 解 相应的 Matlab 程序为 >>t=-0.5*pi:pi/500:1.5*pi; r=100*(2-sin(7*t)-1/2*cos(30*t))./(100+(t-1/2*pi).^8); polar(t,r,'p') %'p'表示用五角星符标志图中数据点 运行后画出图形,见图 1-38,如果改变参数 a ,b ,将会得到很多有趣的图形. 图 1-4 函数 8 100[2 sin( ) 0.5cos( )] 100 ( 0.5 ) a b − − = + − 的图形 二、一元函数极限的计算 除数值计算外,像函数极限、积分、微分、公式推导、因式分解等这一类含有 x ,y ,z
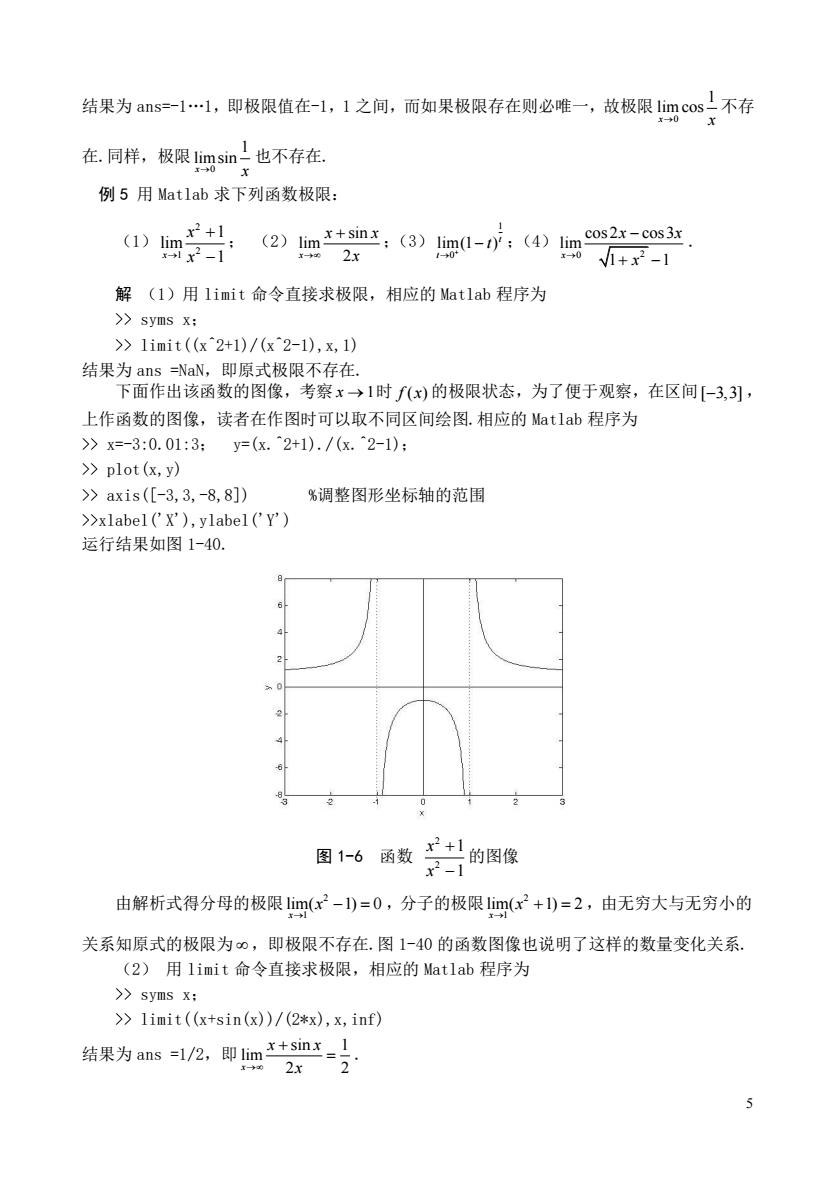
等符号变量的符号表达式的抽象运算,以及求解代数方程或微分方程的精确解等,在工程和 科学研究中占有很大比例.符号表达式是代表数字、函数、算子和变量的Matlab字符串、字 符串数组,不要求变量有预先确定的值.符号方程式是含有符号的表达式.符号计算是使用已 知的规则和给定恒等式求解符号方程的过程,它与代数和微积分所学到的求解方法完全 样.Matlab使用syms这个函数命令来创建和定义基本的符号对象.其调用格式为: syms Varl Var2·Varn Matlab中求函数极限的命令及调用格式如下: limit(s,n,inf) 返回符号表达式当n趋于无穷大时表达式s的极限 limit(s,x,a) 返回符号表达式当x趋于a时表达式s的极限 limit(s) 返回符号表达式中独立变量趋于0时s的极限 limit(s,x,a,'left') 返回符号表达式当x趋于a时表达式s的左极限 limit(s,x,a,'right')返回符号表达式当x趋于a时表达式s的右极限 例4判断极限c0s子sm的存在性 解首先分别作出函数y=cos在区间[-1,-0.010.01,-1-0.001,0.001,等 区间上的图形,观察图形在点x=0附近的形状.在区间[-l,O.0川绘图的Matlab程序为 >x=(-1):0.0001:(-0.01):y=cos(1./x):plot(x,y) 运行结果如图1-39.同样,可作出函数)y=m在点x=0附近的图形 根据图形,能否判断极限c0s子一sn的存在性? 1 09007060504030 图1-5函数y=cos-的图形 当然,也可用limit命令直接求极限,相应的Matlab程序为 >>clear; >syms x: %说明x为符号变量 >limit(cos(1/x),x,0)
4 等符号变量的符号表达式的抽象运算,以及求解代数方程或微分方程的精确解等,在工程和 科学研究中占有很大比例.符号表达式是代表数字、函数、算子和变量的 Matlab 字符串、字 符串数组,不要求变量有预先确定的值.符号方程式是含有符号的表达式.符号计算是使用已 知的规则和给定恒等式求解符号方程的过程,它与代数和微积分所学到的求解方法完全一 样.Matlab 使用 syms 这个函数命令来创建和定义基本的符号对象.其调用格式为: syms Var1 Var2 . Varn Matlab 中求函数极限的命令及调用格式如下: limit(s,n,inf) 返回符号表达式当 n 趋于无穷大时表达式 s 的极限 limit(s,x,a) 返回符号表达式当 x 趋于 a 时表达式 s 的极限 limit(s) 返回符号表达式中独立变量趋于 0 时 s 的极限 limit(s,x,a, 'left') 返回符号表达式当 x 趋于 a -时表达式 s 的左极限 limit(s,x,a, 'right') 返回符号表达式当 x 趋于 a +时表达式 s 的右极限 例 4 判断极限 0 1 lim cos x→ x , 0 1 limsin x→ x 的存在性. 解 首先分别作出函数 1 y cos x = 在区间 [ 1, 0.01] − − ,[0.01,1],[ 1, 0.001] − − ,[0.001,1] 等 区间上的图形,观察图形在点 x = 0 附近的形状.在区间 [ 1, 0.01] − − 绘图的 Matlab 程序为 >> x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 运行结果如图 1-39.同样,可作出函数 1 y sin x = 在点 x = 0 附近的图形. 根据图形,能否判断极限 0 1 lim cos x→ x , 0 1 limsin x→ x 的存在性? 图 1-5 函数 1 y cos x = 的图形 当然,也可用 limit 命令直接求极限,相应的 Matlab 程序为 >> clear; >> syms x; %说明 x 为符号变量 >> limit(cos(1/x),x,0)
结果为ams=一-1.l,即极限值在-1,1之间,而如果极限存在则必唯一,故极限1mc0s不存 在.同样,极限imsin-也不存在。 例5用Matlab求下列函数极限: 2x 1+x2-1 解(1)用limit命令直接求极限,相应的latlab程序为 >syms x: >1imit(x^2+1)/(x^2-1),x,1) 结果为ans=NaN,即原式极限不存在. 下面作出该函数的图像,考察x→1时fx)的极限状态,为了便于观察,在区间-3,3 上作函数的图像,读者在作图时可以取不同区间绘图.相应的Matlab程序为 >x=-3:0.01:3:y=(x.2+1)./(x.2-1): >plot (x.v) >axis([-3,3,-8,8]) %调整图形坐标轴的范围 >>xlabel('X'),ylabel('Y') 运行结果如图1-40. 国16函数的图除 由解析式得分母的极限四(2-)=0,分子的极限(+)=2,由无穷大与无穷小的 关系知原式的极限为,即极限不存在.图1-40的函数图像也说明了这样的数量变化关系, (2)用limit命令直接求极限,相应的Matlab程序为 >》5ym5X: >limit((x+sin(x))(2*x),x,inf) 结果为s即-号 5
5 结果为 ans=-1.1,即极限值在-1,1 之间,而如果极限存在则必唯一,故极限 0 1 lim cos x→ x 不存 在.同样,极限 0 1 limsin x→ x 也不存在. 例 5 用 Matlab 求下列函数极限: (1) 2 2 1 1 lim x 1 x → x + − ; (2) sin lim x 2 x x → x + ;(3) 1 0 lim(1 )t t t → + − ;(4) 0 2 cos 2 cos3 lim 1 1 x x x x → − + − . 解 (1)用 limit 命令直接求极限,相应的 Matlab 程序为 >> syms x; >> limit((x^2+1)/(x^2-1),x,1) 结果为 ans =NaN,即原式极限不存在. 下面作出该函数的图像,考察 x →1 时 f x( ) 的极限状态,为了便于观察,在区间 [ 3,3] − , 上作函数的图像,读者在作图时可以取不同区间绘图.相应的 Matlab 程序为 >> x=-3:0.01:3; y=(x.^2+1)./(x.^2-1); >> plot(x,y) >> axis([-3,3,-8,8]) %调整图形坐标轴的范围 >>xlabel('X'),ylabel('Y') 运行结果如图 1-40. 图 1-6 函数 2 2 1 1 x x + − 的图像 由解析式得分母的极限 2 1 lim( 1) 0 x x → − = ,分子的极限 2 1 lim( 1) 2 x x → + = ,由无穷大与无穷小的 关系知原式的极限为 ,即极限不存在.图 1-40 的函数图像也说明了这样的数量变化关系. (2) 用 limit 命令直接求极限,相应的 Matlab 程序为 >> syms x; >> limit((x+sin(x))/(2*x),x,inf) 结果为 ans =1/2,即 sin 1 lim x 2 2 x x → x + =

(3)用limit命令直接求极限,相应的Matlab程序为 >syms t: >1imit(1-t)^(1/t),t,0,'right') 结果为as=em0,即ml-e (4)用1imit命令直接求极限,相应的Matlab程序为 >syms x: >1imit(cos(2*x)-cos(3*x)/(sqrt(1+x^2)-1),x,0) 结果为即5 注意:Mat1b同其他数学软件一样,进行极限、导数、积分等运算时,都不能给出运算 的中间过程,如果仅仅不明就里地求出了运算结果,这样的学习是没有意义的,所以在使用 软件计算时,千万不能忽视数学课程的学习.我们一再强调的是:软件应用不应该也不能代 替数学课程的学习. 三、作图观察函数的连续性 例6考察下列函数在x=0点的连续性.若是间断点,说明其类型. x2,x0 解首先作出分段函数在区间[-4,4]上的图形,观察图形在点x=0附近的形状.相应的 Matlab程序为 >x1=-4:0.01:0:y1=x1.^2 >x2=0:0.01:4:y2=2: >>plot(x1,yl,x2,y2) 运行结果如图1-41.从函数图像上可以明显看出x=0点是间断点,且在x=0处左右极限存 在但不相等,所以x=0点是第一类间断点中的跳跃间断点】 图1-7分段函数图 6
6 (3) 用 limit 命令直接求极限,相应的 Matlab 程序为 >> syms t; >> limit((1-t)^(1/t),t,0,'right') 结果为 ans = exp(-1),即 1 1 0 1 lim(1 ) e e t t t + − → − = = . (4)用 limit 命令直接求极限,相应的 Matlab 程序为 >> syms x; >> limit((cos(2*x)-cos(3*x))/(sqrt(1+x^2)-1),x,0) 结果为 ans =5,即 0 2 cos 2 cos3 lim 5 1 1 x x x x → − = + − . 注意:Matlab 同其他数学软件一样,进行极限、导数、积分等运算时,都不能给出运算 的中间过程,如果仅仅不明就里地求出了运算结果,这样的学习是没有意义的,所以在使用 软件计算时,千万不能忽视数学课程的学习.我们一再强调的是:软件应用不应该也不能代 替数学课程的学习. 三、作图观察函数的连续性 例 6 考察下列函数在 x = 0 点的连续性.若是间断点,说明其类型. 2 , 0 ( ) 0, 0 2, 0 x x f x x x = = 解 首先作出分段函数在区间 [ 4,4] − 上的图形,观察图形在点 x = 0 附近的形状.相应的 Matlab 程序为 >>x1=-4:0.01:0;y1=x1.^2; >>x2=0:0.01:4;y2=2; >>plot(x1,y1,x2,y2) 运行结果如图 1-41.从函数图像上可以明显看出 x = 0 点是间断点,且在 x = 0 处左右极限存 在但不相等,所以 x = 0 点是第一类间断点中的跳跃间断点. 图 1-7 分段函数图