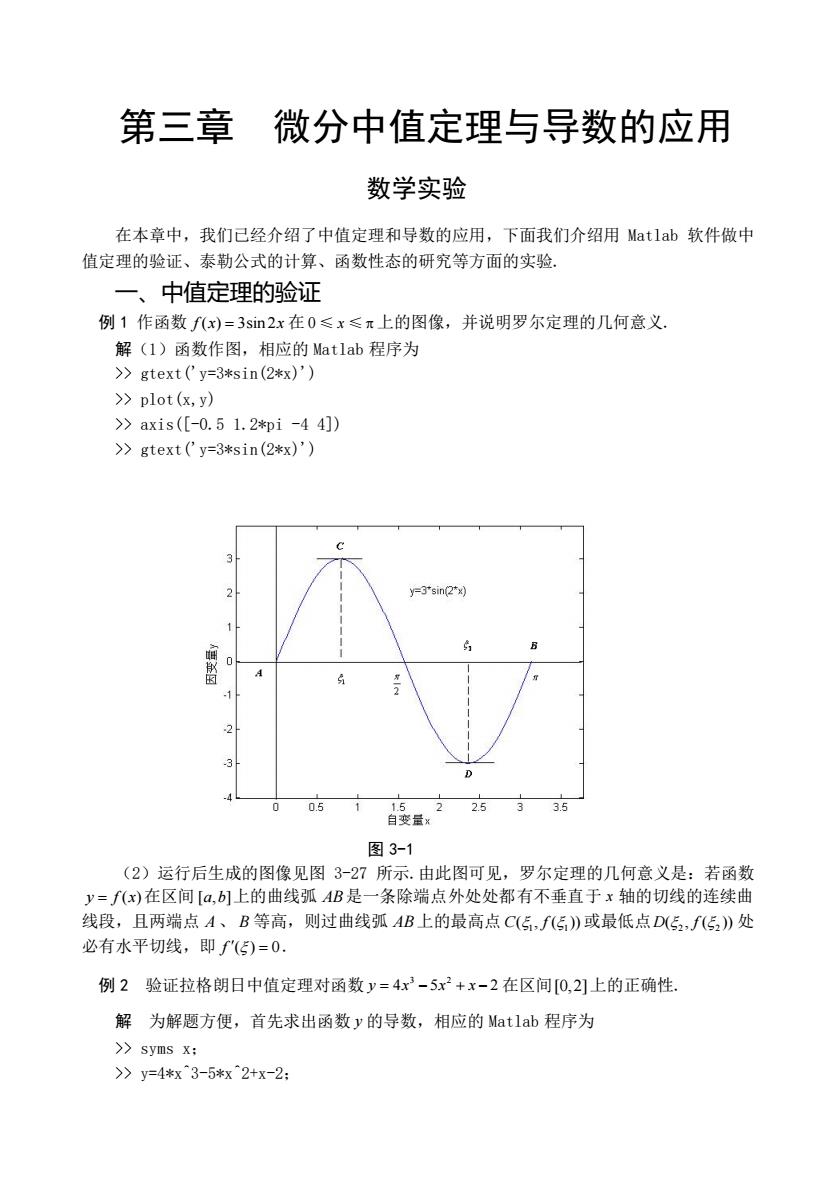
第三章 微分中值定理与导数的应用 数学实验 在本章中,我们己经介绍了中值定理和导数的应用,下面我们介绍用Mat1ab软件做中 值定理的验证、泰勒公式的计算、函数性态的研究等方面的实验。 一、中值定理的验证 例1作函数f(x)-3sin2x在0≤x≤π上的图像,并说明罗尔定理的几何意义. 解(1)函数作图,相应的Matlab程序为 >gtext ('y=3*sin(2*x)') >plot(x,y) >axis([-0.51.2*pi-44]) >gtext('y=3*sin(2*x)') y=3"sin(2x) A 05 25 3 35 图3-1 (2)运行后生成的图像见图3-27所示.由此图可见,罗尔定理的几何意义是:若函数 y=f(x)在区间[a,b]上的曲线弧AB是一条除端点外处处都有不垂直于x轴的切线的连续曲 线段,且两端点A、B等高,则过曲线弧AB上的最高点C(,fG》或最低点D(5,f5》处 必有水平切线,即”()=0. 例2验证拉格朗日中值定理对函数y=4x2-5x2+x-2在区间0,2】上的正确性. 解为解题方便,首先求出函数y的导数,相应的fatlab程序为 >syms x: >》y=4*x^3-5*x^2+x-2:
第三章 微分中值定理与导数的应用 数学实验 在本章中,我们已经介绍了中值定理和导数的应用,下面我们介绍用 Matlab 软件做中 值定理的验证、泰勒公式的计算、函数性态的研究等方面的实验. 一、中值定理的验证 例 1 作函数 f x x ( ) 3sin 2 = 在 0 ≤ x ≤ 上的图像,并说明罗尔定理的几何意义. 解(1)函数作图,相应的 Matlab 程序为 >> gtext('y=3*sin(2*x)') >> plot(x,y) >> axis([-0.5 1.2*pi -4 4]) >> gtext('y=3*sin(2*x)') 图 3-1 (2)运行后生成的图像见图 3-27 所示.由此图可见,罗尔定理的几何意义是:若函数 y f x = ( ) 在区间 [ , ] a b 上的曲线弧 AB 是一条除端点外处处都有不垂直于 x 轴的切线的连续曲 线段,且两端点 A 、 B 等高,则过曲线弧 AB 上的最高点 1 1 C f ( , ( )) 或最低点 2 2 D f ( , ( )) 处 必有水平切线,即 f ( ) 0 = . 例 2 验证拉格朗日中值定理对函数 3 2 y x x x = − + − 4 5 2 在区间 [0,2] 上的正确性. 解 为解题方便,首先求出函数 y 的导数,相应的 Matlab 程序为 >> syms x; >> y=4*x^3-5*x^2+x-2;

>dy=diff(y) 结果为dy=12*x2-10*x+1,接下来利用该结果来验证拉格朗日中值定理,输入程序 >》a=0:b=2:.ya=4*阳3-5*a^2+a-2:yb=4籼^3-5b^2+b-2:%求端点处函数值 >mm=solve(C12*x^2-10*x+1-(yb-ya)/(b-a)=0,x)%求解中值点5的符号解 >m=subs(mm,'[a,b,yb,ya]',[0,2,yb,ya])%代入端点值,求数值解 结果为mm= -0.4041 1.2374 从以上实验结果中可以看到存在一个5=123740,2引,从而验证了拉格朗日中值定理的 正确性. 二、泰勒公式计算 利用Matlab软件提供的taylor函数可以迅速进行函数泰勒公式的计算,taylor函数的 调用格式如下: r=taylor(f) 求函数/形如.0的泰勒展开式 r =taylor(f,m) 求函数)形如.O的泰勒展开式,其中m为正整数 n! r taylor(f,m,a) 求函数形如空-ar.一的勒展开式其中m为正 n 整数,a为实数 例3求下列函数的麦克劳林展开式: (1)y=lnl+x,m-7: (2)y3+4 c=8, 1 解(1)输入Matlab程序 >syms x >f=1og(1+x) >r=taylor(f,7) 结果为r1=x-1/2*x^2+1/3*x^3-1/4*x4+1/5*x^5-1/6*x6. (2)输入Matlab程序 >syms x >f=1/(5+4*cos(x) >>r=taylor(f,8) 结果为r=1/9+2/81*x^2+5/1458*x4+49/131220*x^6. 例4求下列函数在指定点的泰勒展开式: (1)y=x-5x2+x2-3x+4,0=1.5,m=5(2)y=x2nx,=1,m=4
2 >> dy=diff(y) 结果为 dy =12*x^2-10*x+1,接下来利用该结果来验证拉格朗日中值定理,输入程序 >> a=0; b=2; ya=4*a^3-5*a^2+a-2; yb=4*b^3-5*b^2+b-2; %求端点处函数值 >> mm= solve('12*x^2-10*x+1-(yb-ya)/(b-a)=0',x) %求解中值点 的符号解 >>mm=subs(mm,'[a,b,yb,ya]',[0,2,yb,ya]) %代入端点值,求数值解 结果为 mm = -0.4041 1.2374 从以上实验结果中可以看到存在一个 = 1.2374 [0,2] ,从而验证了拉格朗日中值定理的 正确性. 二、泰勒公式计算 利用 Matlab 软件提供的 taylor 函数可以迅速进行函数泰勒公式的计算,taylor 函数的 调用格式如下: r = taylor(f) 求函数 f x( ) 形如 5 ( ) 0 (0) ! n n n f x = n 的泰勒展开式 r = taylor(f,m) 求函数 f x( ) 形如 ( ) 0 (0) ! m n n n f x = n 的泰勒展开式,其中 m 为正整数 r = taylor(f,m,a) 求函数 f x( ) 形如 ( ) 0 ( ) ( ) ! m n n n f a x a = n − 的泰勒展开式,其中 m 为正 整数, a 为实数 例 3 求下列函数的麦克劳林展开式: (1) y x m = + = ln(1 ), 7 ; (2) 1 , 8 5 4cos y m x = = + . 解(1) 输入 Matlab 程序 >> syms x >> f=log(1+x); >> r=taylor(f,7) 结果为 r1 =x-1/2*x^2+1/3*x^3-1/4*x^4+1/5*x^5-1/6*x^6. (2)输入 Matlab 程序 >> syms x >> f=1/(5+4*cos(x)); >> r=taylor(f,8) 结果为 r =1/9+2/81*x^2+5/1458*x^4+49/131220*x^6. 例 4 求下列函数在指定点的泰勒展开式: (1) 4 3 2 0 y x x x x x m = − + − + = = 5 3 4, 1.5, 5 ;(2) 2 0 y x x x m = = = ln , 1, 4
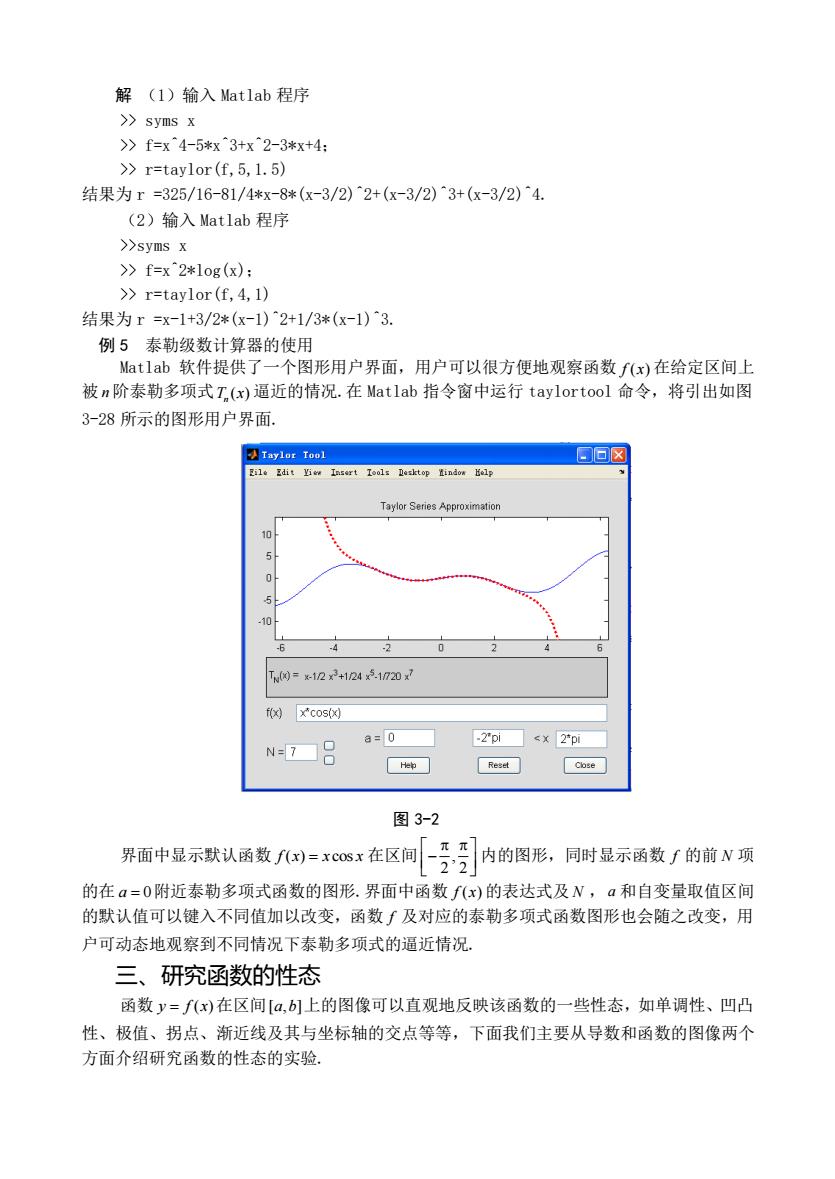
解(1)输入Matlab程序 >sVms x >》f=x4-5*x^3+x^2-3*x+4 >r=taylor(f,5,1.5) 结果为r=325/16-81/4*x-8*(x-3/2)^2+(x-3/2)^3+(x-3/2)^4. (2)输入Matlab程序 >>syms x >》f=x^2*10g(x): >>r=taylor(f,4,1) 结果为r=x-1+3/2*(x-1)2+1/3*(x-1)3. 例5泰勒级数计算器的使用 Matlab软件提供了 个图形用户界面,用户可以很方便地观察函数∫x)在给定区间上 被n阶泰勒多项式T,(x)逼近的情况.在Matlab指令窗中运行taylortool命令,将引出如图 3-28所示的图形用户界面. 日▣☒ Zile Elit yee Intert Zoals Desktep tindow Help T网=x122+12451720 f例cosx) N=79 8=0 -2"pi <x 2"pi e电 Resst Close 图3-2 界面中显示玖认爵数-0:在区间[引内的图形,同时是示函数∫的前N项 的在a=0附近泰勒多项式函数的图形.界面中函数∫(x)的表达式及N,,a和自变量取值区间 的默认值可以键入不同值加以改变,函数∫及对应的泰勒多项式函数图形也会随之改变,用 户可动态地观察到不同情况下泰勒多项式的逼近情况 三、研究函数的性态 函数y=f(x)在区间[a,b上的图像可以直观地反映该函数的一些性态,如单调性、凹凸 性、极值、拐点、渐近线及其与坐标轴的交点等等,下面我们主要从导数和函数的图像两个 方面介绍研究函数的性态的实验
解 (1)输入 Matlab 程序 >> syms x >> f=x^4-5*x^3+x^2-3*x+4; >> r=taylor(f,5,1.5) 结果为 r =325/16-81/4*x-8*(x-3/2)^2+(x-3/2)^3+(x-3/2)^4. (2)输入 Matlab 程序 >>syms x >> f=x^2*log(x); >> r=taylor(f,4,1) 结果为 r =x-1+3/2*(x-1)^2+1/3*(x-1)^3. 例 5 泰勒级数计算器的使用 Matlab 软件提供了一个图形用户界面,用户可以很方便地观察函数 f x( ) 在给定区间上 被 n 阶泰勒多项式 ( ) T x n 逼近的情况.在 Matlab 指令窗中运行 taylortool 命令,将引出如图 3-28 所示的图形用户界面. 图 3-2 界面中显示默认函数 f x x x ( ) cos = 在区间 , 2 2 − 内的图形,同时显示函数 f 的前 N 项 的在 a = 0 附近泰勒多项式函数的图形.界面中函数 f x( ) 的表达式及 N ,a 和自变量取值区间 的默认值可以键入不同值加以改变,函数 f 及对应的泰勒多项式函数图形也会随之改变,用 户可动态地观察到不同情况下泰勒多项式的逼近情况. 三、研究函数的性态 函数 y f x = ( ) 在区间 [ , ] a b 上的图像可以直观地反映该函数的一些性态,如单调性、凹凸 性、极值、拐点、渐近线及其与坐标轴的交点等等,下面我们主要从导数和函数的图像两个 方面介绍研究函数的性态的实验

例6求解函数fx)=x2+6x2+12x+4的单调性、凹凸性、极值和拐点. 解首先求解函数的一、二阶导数,然后画出它们的图像,最后利用图像研究该函数的 性态.相应的Matlab程序如下: >syms x: >>f=x3-6*x"2+12*x+4 >fl=diff(f,x) >f2=diff(f1,x) >f1jie=solve(fL,'x')%求驻点 >>x=-3:057. >>y=subs(f,'x',x) %代入自变量x的取值,求y=x)函数值 >》yl=subs(f1,’x',x):%代入自变量x,求导函数y=f'(x)的值 >》y2=subs(f2,'x',x):%代入自变量x,求导函数y=f"(x)的值 >hold on >plot(x,y) %绘制函数y=fx)的图像 >》plot(x,yl,’-.k')%绘制函数的y=f"(x)图像 》plot(x,y2,’一r'):%绘制函数的y=f(x)图像 >》grid on%加上网格线,为方便观察函数性态 相应输出函数的一阶、二阶导数 150 表达式及驻点如下,三个函数图像如 图3-29所示 f1=3*x2-12*x+12 f2=6*x-12 fljie= 2 2 由fx),fx),f"(x)这三个函 数的图像可以看到:当x∈R时,总 有(x)≥0(黑色点划线),所以 (-.+0)是f(x)的单调递增区间,又 4 图3-3 由于f(x)不变号,所以函数没有极值点和极值:又当x∈(-m,2)时,f"(0,所以(-,2)是f(x)的四区间,而(2,+o)是fx)的凸区间,又有f2)=0,因 此(2,12)为函数f(x)的拐点
4 例 6 求解函数 3 2 f x x x x ( ) 6 12 4 = + + + 的单调性、凹凸性、极值和拐点. 解 首先求解函数的一、二阶导数,然后画出它们的图像,最后利用图像研究该函数的 性态.相应的 Matlab 程序如下: >> syms x; >> f=x^3-6*x^2+12*x+4; >> f1=diff(f,x) >> f2=diff(f1,x) >> f1jie=solve(f1,'x') %求驻点 >> x=-3:0.5:7; >> y=subs(f,'x',x); %代入自变量 x 的取值,求 y f x = ( ) 函数值 >> y1=subs(f1,'x',x); %代入自变量 x ,求导函数 y f x = ( ) 的值 >> y2=subs(f2,'x',x); %代入自变量 x ,求导函数 y f x = ( ) 的值 >> hold on >> plot(x,y); %绘制函数 y f x = ( ) 的图像 >> plot(x,y1,'-.k') %绘制函数的 y f x = ( ) 图像 >> plot(x,y2,'-r'); %绘制函数的 y f x = ( ) 图像 >> grid on %加上网格线,为方便观察函数性态 相应输出函数的一阶、二阶导数 表达式及驻点如下,三个函数图像如 图 3-29 所示. f1 =3*x^2-12*x+12 f2 =6*x-12 f1jie = 2 2 由 f x( ),f x ( ), f x ( ) 这三个函 数的图像可以看到:当 x R 时,总 有 f x ( ) ≥ 0 (黑色点划线),所以 ( , ) − + 是 f x( ) 的单调递增区间,又 图 3-3 由于 f x ( ) 不变号,所以函数没有极值点和极值;又当 x − ( ,2) 时, f x ( ) 0 ,当 x + (2, ) 时, f x ( ) 0 ,所以 ( ,2) − 是 f x( ) 的凹区间,而 (2, ) + 是 f x( ) 的凸区间,又有 f (2) 0 = ,因 此 (2,12) 为函数 f x( ) 的拐点