
重点:对弧长的曲线积分及计算方法 难点:计算方法 关键:定义与曲线方程的表达 相关知识:微元素法、平面曲线积分的计算 授课内容 2012329 泰山医学院信息工程学院高等数学教研室

第一节对弧长的曲线积分 -、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法 三、小结 2012-3-29 泰山医学院信息工程学院高等数学教研室 2
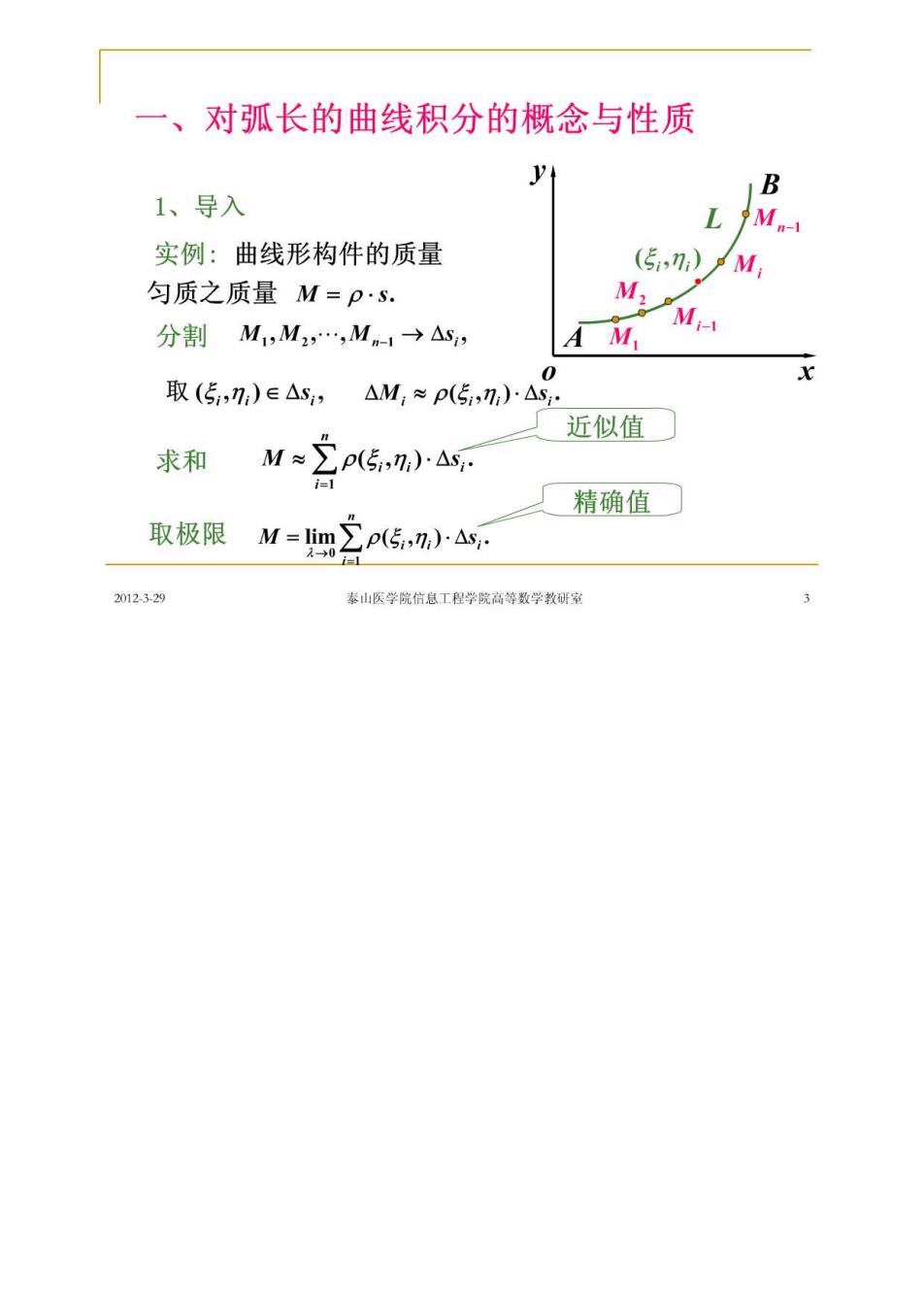
一、对弧长的曲线积分的概念与性质 y B 1、导入 实例:曲线形构件的质量 (5,n)M 匀质之质量M=ps. 分割M1,M,Mn1→△s, A M M 取(5,n)∈△s1, △M,*P(,-A号 一近似值○ 求和 W~2G,2-4 取极限M=m之p5,)a 精确值口 2012329 泰山医学院信息工程学院高等数学教研室
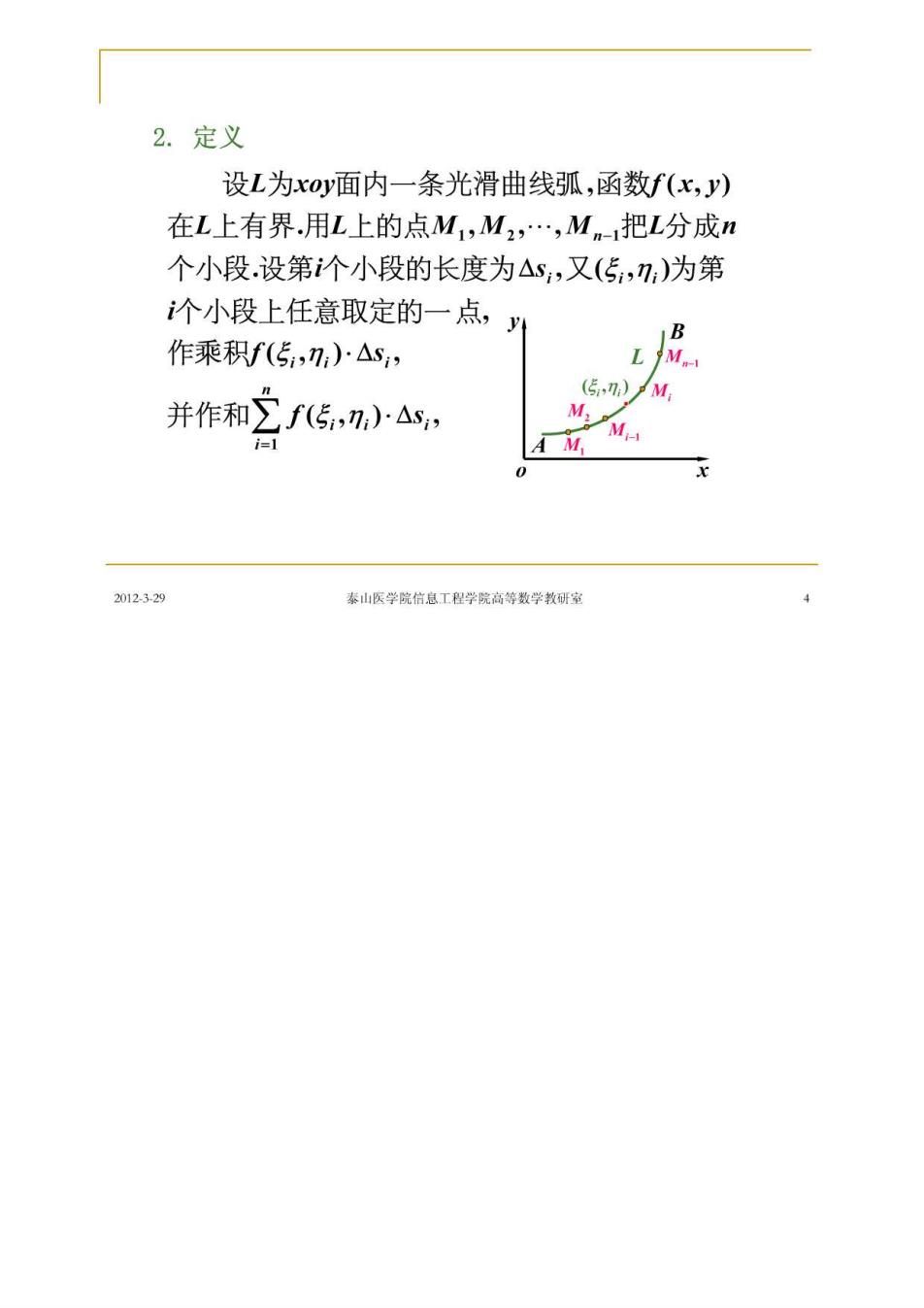
2.定义 设L为x0y面内一条光滑曲线弧,函数f(x,y) 在L上有界.用L上的点M1,M2,Mn-把L分成n 个小段.设第个小段的长度为△s,又(5,)为第 个小段上任意取定的一点, 作乘积f(5,n,)△s, L M. 并作和2f5,n,)△, (5,n)M M: AM M 2012329 泰山医学院信息工程学院高等数学教研室

如果当各小弧段的长度的最大值入→0时, 这和的极限存在,则称此极限为函数f(x,y) 在曲线弧L上对弧长的曲线积分或第一类曲 线积分,记作[f(x,y)ds,即 积分和式 被积函数 f().As 积分弧段 曲线形构件的质量M=∫p(x,Jy)d. 2012329 泰山医学院信息工程学院高等数学教研室

3.存在条件: 当f(x,y)在光滑曲线弧L上连续时,对弧长的曲线积分 ∫f(x,y)存在. 4.推广: 函数f(x,y,)在空间曲线弧T上对弧长的曲线积分为 [f(x.y.ds=m)As 2012329 泰山医学院信息工程学院高等数学教研室

注意: 1.若L(或T)是分段光滑的,(L=L,+) Lxk=fxh+Lfx,. 2.函数f(x,y)在闭曲线L上对弧长的曲线积分记为 f(x,y)ds. 2012329 素山医学院信息工程学院高等数学教研室

5.性质 (四fx,)±gc,s=fx,J)±g(x,)s. (2)∫f(x,)=kf(x,)(k为常数). (3)[f(x,y)ds=[f(x,y)ds+f(x,y)ds. (L=L+L2) 2012329 泰山医学院信息工程学院高等数学教研室

二、对弧长的曲线积分的计算方法 1、计算方法 定理设f(x,y)在曲线弧L上有定义且连续,L的参数 方程为r=p, (a≤1≤B)其中p(t),w()在[a,B]上 y=v(t), 具有一阶连续导数,则 If(x,y)ds=[f(t).v(t"()+v"(t)di (a<B) 2012329 素山医学院信息工程学院高等数学教研室

注意: 1.定积分的下限a一定要小于上限B: 2.f(x,y)中x,y不彼此独立,而是相互有关的. 特殊情形 (1)L:y=v(x) a≤x≤b. [f(x,y)ds=[flx,v(x)+V(xdx.(a<b) 2012329 泰山医学院信息工程学院高等数学教研室