
第三章检测 一、选择题(每小题4分,共32分) 1.已知⊙O与直线AB相交,且圆心O到直线AB的距离是方程2x-1=4的根,则 ⊙0的半径可以为) A.1 B.2 C.2.5 D.3 2.如图,AB,CD是⊙0的直径,AE=BD,若∠AOE=32°,则∠COE的度数是() A.32 B.60° C.68 D.64° 3.(2022贵州贵阳中考)如图,己知∠ABC=60°,点D为BA边上一点,BD=10,点O 为线段BD的中点,以点O为圆心,线段OB的长为半径作弧,交BC于点E,连接 DE,则BE的长是() E A.5 B.5V2 C.5v3 D.5v5 4如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线 交于A,B两点,他测得图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处 位置到太阳完全跳出海平面的时间为16分钟,则图上”太阳升起的速度为() A.1.0厘米分 B.0.8厘米/分 C.1.2厘米/分 D.1.4厘米/分 5.如图,边长为2v3的等边△ABC的内切圆的半径为) A.1 B.v3 C.2 D.2v3
第三章检测 一、选择题(每小题 4 分,共 32 分) 1.已知☉O 与直线 AB 相交,且圆心 O 到直线 AB 的距离是方程 2x-1=4 的根,则 ☉O 的半径可以为( ). A.1 B.2 C.2.5 D.3 2.如图,AB,CD 是☉O 的直径,𝐴𝐸⏜ = 𝐵𝐷⏜ ,若∠AOE=32°,则∠COE 的度数是( ). A.32° B.60° C.68° D.64° 3.(2022·贵州贵阳中考)如图,已知∠ABC=60°,点 D 为 BA 边上一点,BD=10,点 O 为线段 BD 的中点,以点 O 为圆心,线段 OB 的长为半径作弧,交 BC 于点 E,连接 DE,则 BE 的长是( ). A.5 B.5√2 C.5√3 D.5√5 4.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线 交于 A,B 两点,他测得“图上”圆的半径为 10 厘米,AB=16 厘米.若从目前太阳所处 位置到太阳完全跳出海平面的时间为 16 分钟,则“图上”太阳升起的速度为( ). A.1.0 厘米/分 B.0.8 厘米/分 C.1.2 厘米/分 D.1.4 厘米/分 5.如图,边长为 2√3的等边△ABC 的内切圆的半径为( ). A.1 B.√3 C.2 D.2√3
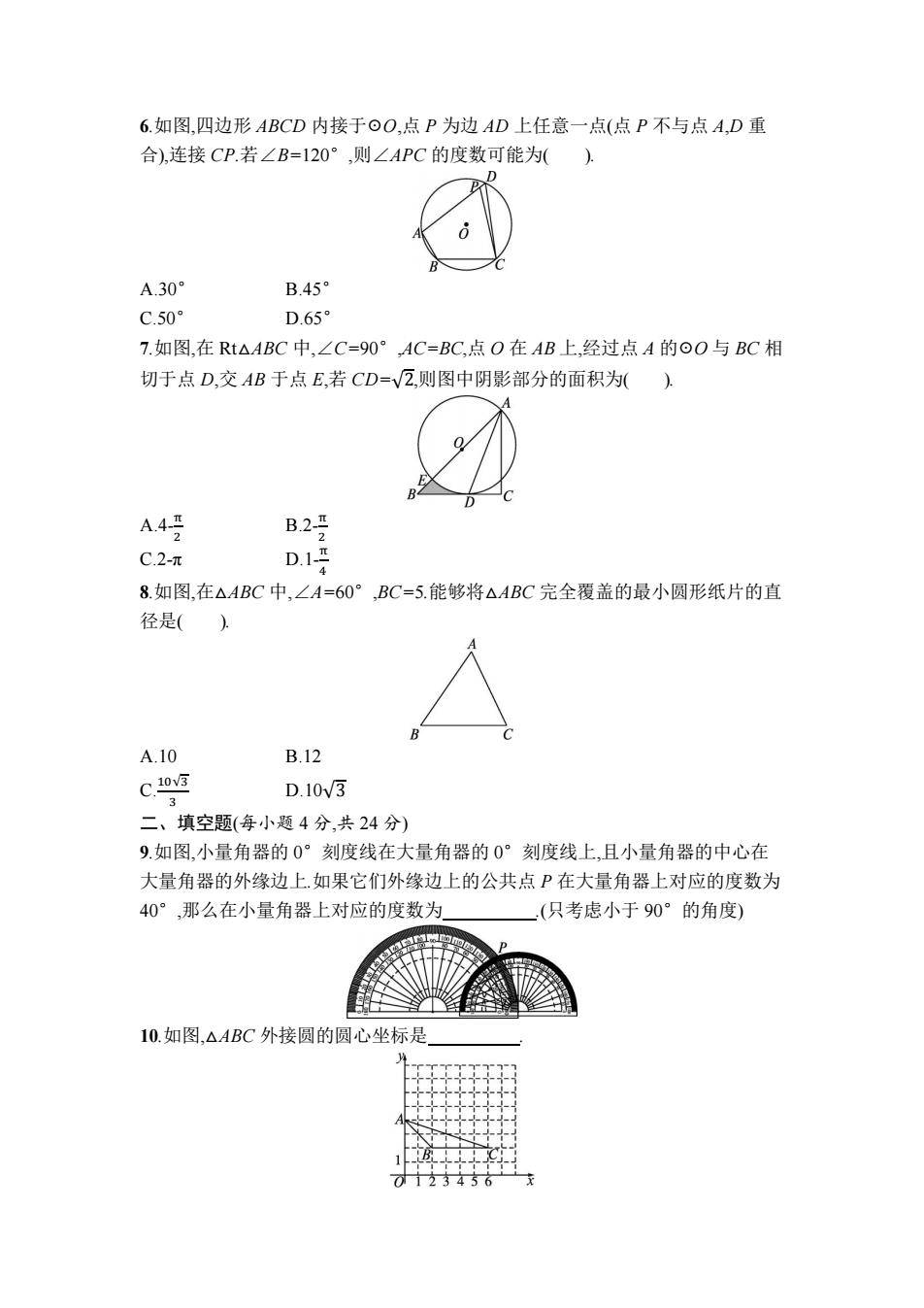
6.如图,四边形ABCD内接于⊙O,点P为边AD上任意一点(点P不与点A,D重 合),连接CP.若∠B=120°,则∠APC的度数可能为( ). A.30° B.45° C.50 D.65° 7.如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相 切于点D,交AB于点E,若CD=√Z,则图中阴影部分的面积为() A.48 B.2-π C.2-π D.13 8.如图,在△ABC中,∠A=60°,BC=5.能够将△ABC完全覆盖的最小圆形纸片的直 径是() A.10 B.12 C.03 D.10v3 3 二、填空题(每小题4分,共24分) 9.如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在 大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为 40°,那么在小量角器上对应的度数为 (只考虑小于90°的角度) 10.如图,△ABC外接圆的圆心坐标是 0123456
6.如图,四边形 ABCD 内接于☉O,点 P 为边 AD 上任意一点(点 P 不与点 A,D 重 合),连接 CP.若∠B=120°,则∠APC 的度数可能为( ). A.30° B.45° C.50° D.65° 7.如图,在 Rt△ABC 中,∠C=90°,AC=BC,点 O 在 AB 上,经过点 A 的☉O 与 BC 相 切于点 D,交 AB 于点 E,若 CD=√2,则图中阴影部分的面积为( ). A.4- π 2 B.2- π 2 C.2-π D.1- π 4 8.如图,在△ABC 中,∠A=60°,BC=5.能够将△ABC 完全覆盖的最小圆形纸片的直 径是( ). A.10 B.12 C. 10√3 3 D.10√3 二、填空题(每小题 4 分,共 24 分) 9.如图,小量角器的 0°刻度线在大量角器的 0°刻度线上,且小量角器的中心在 大量角器的外缘边上.如果它们外缘边上的公共点 P 在大量角器上对应的度数为 40°,那么在小量角器上对应的度数为 .(只考虑小于 90°的角度) 10.如图,△ABC 外接圆的圆心坐标是

11.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15°,弦CD=4,那么AB的 长是 12.如图,PA,PB分别与⊙O相切于A,B两点,PO与AB相交于点C,PA=6, ∠APB=60°,则OC的长为 13.如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则 弦AB所对的圆周角的度数是 14.己知直线y=(0)经过点(12,-5),将直线向上平移m(m>0)个单位,若平移后得 到的直线与半径为6的⊙0相交(点0为坐标原点),则m的取值范围为 三、解答题(共44分) 15.(8分)如图,某广场改造后安装了八个大理石球.小明想知道其中一个球的半径, 于是找了两块厚10cm的砖塞在球的两侧,并量得两砖之间的距离是60cm.请你 在图中利用所学的几何知识,求出大理石球的半径.(要写出计算过程) 5 16.(8分)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连 接BC (I)求证:AE=ED: (2)若AB=10,∠CBD=36°,求劣弧AC的长. 17.(8分)如图,己知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F, 交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF
11.如图,AB 是☉O 的直径,弦 CD⊥AB 于点 E,如果∠A=15°,弦 CD=4,那么 AB 的 长是 . 12.如图,PA,PB 分别与☉O 相切于 A,B 两点,PO 与 AB 相交于点 C,PA=6, ∠APB=60°,则 OC 的长为 . 13.如图,☉O 的半径是 2,AB 是☉O 的弦,点 P 是弦 AB 上的动点,且 1≤OP≤2,则 弦 AB 所对的圆周角的度数是 . 14.已知直线 y=kx(k≠0)经过点(12,-5),将直线向上平移 m(m>0)个单位,若平移后得 到的直线与半径为 6 的☉O 相交(点 O 为坐标原点),则 m 的取值范围为 . 三、解答题(共 44 分) 15.(8 分)如图,某广场改造后安装了八个大理石球.小明想知道其中一个球的半径, 于是找了两块厚 10 cm 的砖塞在球的两侧,并量得两砖之间的距离是 60 cm.请你 在图中利用所学的几何知识,求出大理石球的半径.(要写出计算过程) 16.(8 分)如图,已知 AB 是☉O 的直径,C,D 是☉O 上的点,OC∥BD,交 AD 于点 E,连 接 BC. (1)求证:AE=ED; (2)若 AB=10,∠CBD=36°,求劣弧𝐴𝐶⏜的长. 17.(8 分)如图,已知 AB 是☉O 的直径,☉O 经过 Rt△ACD 的直角边 DC 上的点 F, 交 AC 边于点 E,点 F 是弧 EB 的中点,∠C=90°,连接 AF
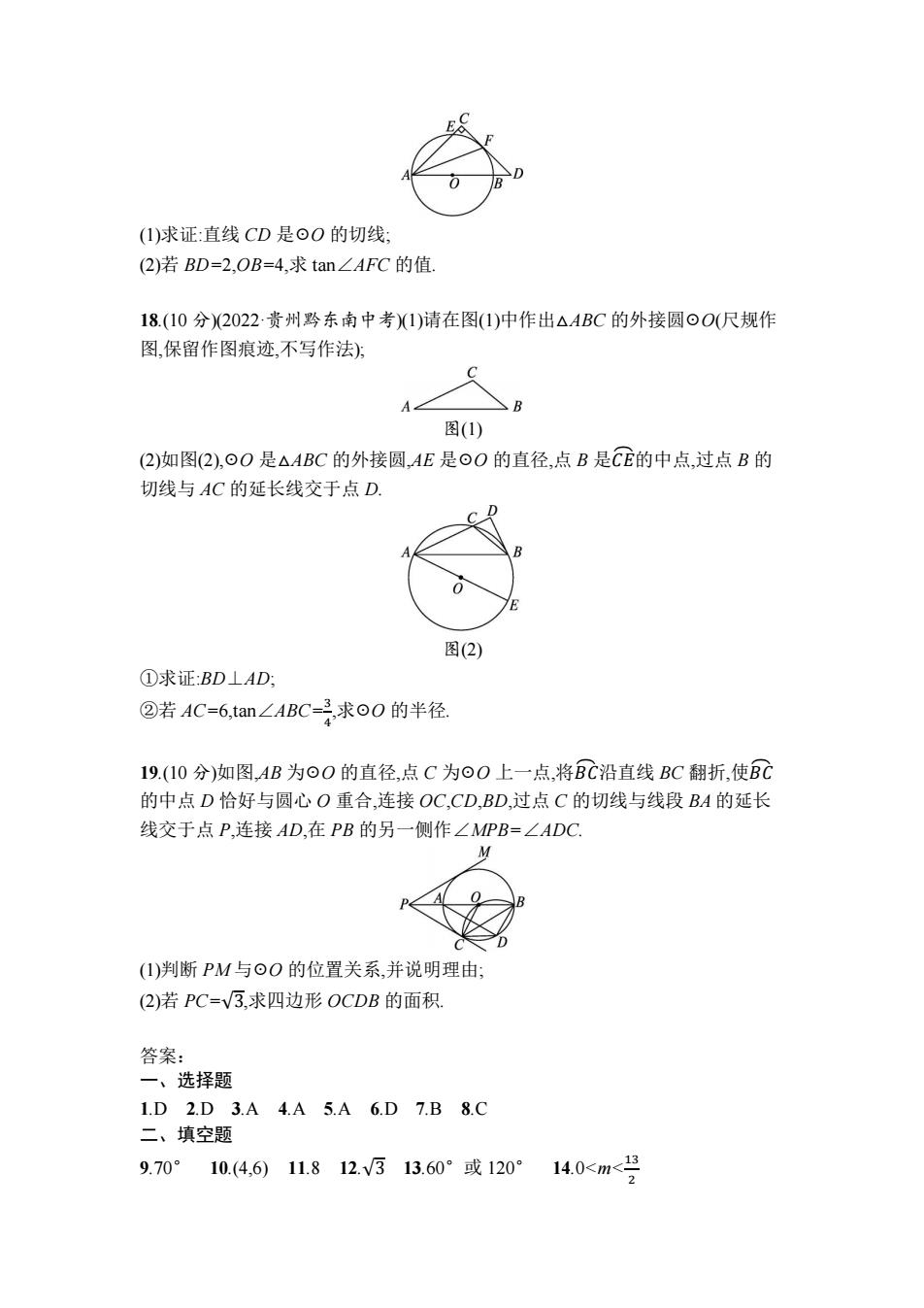
(1)求证:直线CD是⊙O的切线: (2)若BD=2,OB=4,求tan∠AFC的值 18.(10分)2022·贵州黔东南中考)(1)请在图(1)中作出△ABC的外接圆⊙O(尺规作 图,保留作图痕迹,不写作法): 图(1) (2)如图(2),⊙O是△ABC的外接圆,AE是⊙O的直径,点B是CE的中点,过点B的 切线与AC的延长线交于点D. 图(2) ①求证:BD⊥AD: ②若AC=6,tan∠ABC-求o0的半径. 19.(10分)如图,AB为OO的直径,点C为OO上一点,将BC沿直线BC翻折,使BC 的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长 线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC (1)判断PM与⊙O的位置关系,并说明理由; (2)若PC=V3,求四边形OCDB的面积 答案: 一、选择题 1.D2.D3.A4.A5.A6.D7.B8.C 二、填空题 9.70°10.(4,6)11.812.V313.60°或120°14.0<m<5
(1)求证:直线 CD 是☉O 的切线; (2)若 BD=2,OB=4,求 tan∠AFC 的值. 18.(10 分)(2022·贵州黔东南中考)(1)请在图(1)中作出△ABC 的外接圆☉O(尺规作 图,保留作图痕迹,不写作法); 图(1) (2)如图(2),☉O 是△ABC 的外接圆,AE 是☉O 的直径,点 B 是𝐶𝐸⏜的中点,过点 B 的 切线与 AC 的延长线交于点 D. 图(2) ①求证:BD⊥AD; ②若 AC=6,tan∠ABC=3 4 ,求☉O 的半径. 19.(10 分)如图,AB 为☉O 的直径,点 C 为☉O 上一点,将𝐵𝐶⏜ 沿直线 BC 翻折,使𝐵𝐶⏜ 的中点 D 恰好与圆心 O 重合,连接 OC,CD,BD,过点 C 的切线与线段 BA 的延长 线交于点 P,连接 AD,在 PB 的另一侧作∠MPB=∠ADC. (1)判断 PM 与☉O 的位置关系,并说明理由; (2)若 PC=√3,求四边形 OCDB 的面积. 答案: 一、选择题 1.D 2.D 3.A 4.A 5.A 6.D 7.B 8.C 二、填空题 9.70° 10.(4,6) 11.8 12.√3 13.60°或 120° 14.0<m<13 2

三、解答题 15.解:根据题意可以建立圆中垂径定理的模型如图. AC=60cm,BD=10cm,设半径为rcm, ,OB⊥AC ∴.AD=AC=30(cm, 在Rt△ADO中,,AD2+OD2=OA2, .302+(r-102=2 解得r=50(cm). .大理石球的半径为50cm. 16.(1)证明,AB是⊙O的直径, ∴.∠ADB=90° ,OC∥BD .∠AEO=∠ADB=90°, 即OC⊥AD ∴.AE=ED (2)解:OC⊥AD,.AC=CD ∴.∠ABC=∠CBD=36 ∴.∠AOC=2∠ABC=2×36°=72°. AC的长-72mx5=2元 180 17.(1)证明连接OF,BE,如图. ,AB是⊙O的直径 ∴.∠AEB=90 :∠C=90°,∴.∠AEB=∠ACD, ∴.BE∥CD ,点F是孤BE的中点 .OF⊥BE,∴.OF⊥CD ,OF为半径 ∴.直线CD是⊙O的切线」 (2)解:.∠C=∠OFD=90° ∴.AC∥OF,∴.△OFD∽△ACD
三、解答题 15.解:根据题意可以建立圆中垂径定理的模型如图. AC=60 cm,BD=10 cm,设半径为 r cm, ∵OB⊥AC, ∴AD=1 2 AC=30(cm). 在 Rt△ADO 中,∵AD2+OD2=OA2 , ∴302+(r-10)2=r2 , 解得 r=50(cm). ∴大理石球的半径为 50 cm. 16.(1)证明 ∵AB 是☉O 的直径, ∴∠ADB=90°. ∵OC∥BD, ∴∠AEO=∠ADB=90°, 即 OC⊥AD. ∴AE=ED. (2)解:∵OC⊥AD,∴𝐴𝐶⏜ = 𝐶𝐷⏜ . ∴∠ABC=∠CBD=36°. ∴∠AOC=2∠ABC=2×36°=72°. ∴𝐴𝐶⏜的长= 72π×5 180 =2π. 17.(1)证明 连接 OF,BE,如图. ∵AB 是☉O 的直径, ∴∠AEB=90°. ∵∠C=90°,∴∠AEB=∠ACD, ∴BE∥CD. ∵点 F 是弧 BE 的中点, ∴OF⊥BE,∴OF⊥CD. ∵OF 为半径, ∴直线 CD 是☉O 的切线. (2)解:∵∠C=∠OFD=90°, ∴AC∥OF,∴△OFD∽△ACD

柴-岩 .BD=2,0F=OB=4 .OD=6,AD=10, ∴4C-0="=9 OD 6 ∴.CD=VAD2-AC= √102-(92=05 3 .AC∥OF,OA=4, 10v5 票=岩即华=解得C AD 4 3 tam∠AFc-÷-是=v5 18.(1)解:如图(1),⊙O即为△ABC的外接圆 图(1) (2)①证明如图(2),连接OB, 图(2) BD是⊙O的切线, .OB⊥BD :点B是CE的中点, ∴BC=BE ∴.∠CAB=∠EAB. .OA=OB, ∴.∠OBA=∠EAB. ∴.∠CAB=∠OBA. ∴.OB∥AD ∴.BD⊥AD ②解:如图(2),连接EC
∴ 𝑂𝐹 𝐴𝐶 = 𝑂𝐷 𝐴𝐷 . ∵BD=2,OF=OB=4, ∴OD=6,AD=10, ∴AC=𝑂𝐹×𝐴𝐷 𝑂𝐷 = 4×10 6 = 20 3 , ∴CD=√𝐴𝐷2 -𝐴𝐶 2= √10 2 -( 20 3 ) 2 = 10√5 3 . ∵AC∥OF,OA=4, ∴ 𝐶𝐹 𝑂𝐴 = 𝐶𝐷 𝐴𝐷 ,即 𝐶𝐹 4 = 10√5 3 10 ,解得 CF=4√5 3 , ∴tan∠AFC=𝐴𝐶 𝐶𝐹 = 20 3 4√5 3 = √5. 18.(1)解:如图(1),☉O 即为△ABC 的外接圆. 图(1) (2)①证明 如图(2),连接 OB, 图(2) ∵BD 是☉O 的切线, ∴OB⊥BD. ∵点 B 是𝐶𝐸⏜的中点, ∴𝐵𝐶⏜ = 𝐵𝐸⏜ . ∴∠CAB=∠EAB. ∵OA=OB, ∴∠OBA=∠EAB. ∴∠CAB=∠OBA. ∴OB∥AD. ∴BD⊥AD. ②解:如图(2),连接 EC

由圆周角定理得:∠AEC=∠ABC, :tan∠ABC-是 tan∠AEC-月 ,AE是⊙O的直径 .∠ACE=90°, 光=月 ,AC=6 .EC=8. ∴.AE=VAC2+EC2=10. .⊙0的半径为5. 19.解:(1)PM与⊙O相切.理由如下: 如图,连接DO并延长交PM于点E, ,BC沿直线BC翻折,使BC的中点D恰好与圆心O重合 ∴.OC=DC,BO=BD ∴.OC=DC=BO=BD .四边形OBDC为菱形 .OD⊥BC ∴.△OCD和△OBD都是等边三角形. ∴.∠COD=∠BOD=60 ∴.∠COP=∠EOP=60°. ,∠MPB=∠ADC,而∠ADC=∠ABC,∴.∠ABC=∠MPB. ∴.PM∥BC.∴.OE⊥PM ∴.OE=0P .PC为⊙O的切线,∴.OC⊥PC ∴.0C=0P.∴.0E=0C 而OE⊥PM,∴.PM是⊙O的切线,即PM与⊙O相切 (2)在Rt△OPC中,0C=PC=5×V3=1, 四边形0CDB的面积=2Sa0cD=2××12=5 2
由圆周角定理得:∠AEC=∠ABC, ∵tan∠ABC=3 4 , ∴tan∠AEC=3 4 . ∵AE 是☉O 的直径, ∴∠ACE=90°, ∴ 𝐴𝐶 𝐸𝐶 = 3 4 . ∵AC=6, ∴EC=8. ∴AE=√𝐴𝐶 2 + 𝐸𝐶 2=10. ∴☉O 的半径为 5. 19.解:(1)PM 与☉O 相切.理由如下: 如图,连接 DO 并延长交 PM 于点 E, ∵𝐵𝐶⏜ 沿直线 BC 翻折,使𝐵𝐶⏜ 的中点 D 恰好与圆心 O 重合, ∴OC=DC,BO=BD. ∴OC=DC=BO=BD. ∴四边形 OBDC 为菱形. ∴OD⊥BC. ∴△OCD 和△OBD 都是等边三角形. ∴∠COD=∠BOD=60°. ∴∠COP=∠EOP=60°. ∵∠MPB=∠ADC,而∠ADC=∠ABC,∴∠ABC=∠MPB. ∴PM∥BC.∴OE⊥PM. ∴OE=1 2 OP. ∵PC 为☉O 的切线,∴OC⊥PC. ∴OC=1 2 OP.∴OE=OC. 而 OE⊥PM,∴PM 是☉O 的切线,即 PM 与☉O 相切. (2)在 Rt△OPC 中,OC=√3 3 PC=√3 3 × √3=1, ∴四边形 OCDB 的面积=2S△OCD=2× √3 4 ×1 2= √3 2