
第二十四章检测 一、选择题(每小题3分,共30分) 1.如图,已知DC是⊙O的直径,弦AB⊥CD于点F,连接BC,DB,则下列结论不一定 正确的是(C), A.AD-BD B.AF=BF C.OF=CF D.∠DBC=90° 2.如图,AB是⊙O的直径,点C在⊙O上,若∠A=40°,则∠B的度数为(C)】 A.80° B.60° C.50° D.40° 3.如图,P是⊙O外一点,PA是⊙0的切线,若PO=26cm,PA=24cm,则⊙O的周长为 (C). A.18πcm B.16元cm C.20z cm D.24x cm
第二十四章检测 一、选择题(每小题 3 分,共 30 分) 1.如图,已知 DC 是☉O 的直径,弦 AB⊥CD 于点 F,连接 BC,DB,则下列结论不一定 正确的是(C). A.𝐴𝐷⏜=𝐵𝐷⏜ B.AF=BF C.OF=CF D.∠DBC=90° 2.如图,AB 是☉O 的直径,点 C 在☉O 上,若∠A=40°,则∠B 的度数为(C). A.80° B.60° C.50° D.40° 3.如图,P 是☉O 外一点,PA 是☉O 的切线,若 PO=26 cm,PA=24 cm,则☉O 的周长为 (C). A.18π cm B.16π cm C.20π cm D.24π cm

4.如图,已知OA=OB=OC,且∠ACB=30°,则∠AOB的大小是(C) 0 30 A.40° B.50 C.60° D.70° 5.若⊙O1的半径为1cm,⊙O2的半径为4cm,圆心距O1O2=3cm,则两圆的位置关系 是(B) A.相交 B.内切 C.外切 D.内含 6.如图,⊙O的直径AB垂直于弦CD,若∠CAB=36°,则∠BCD的大小是(B) A.18 B.36 C.54° D.72° 7.己知一个三角形的三边长分别为5,7,8,则其内切圆的半径为(C) A号 B C.3 D.2V3
4.如图,已知 OA=OB=OC,且∠ACB=30°,则∠AOB 的大小是(C). A.40° B.50° C.60° D.70° 5.若☉O1的半径为1 cm,☉O2的半径为4 cm,圆心距O1O2=3 cm,则两圆的位置关系 是(B). A.相交 B.内切 C.外切 D.内含 6.如图,☉O 的直径 AB 垂直于弦 CD,若∠CAB=36°,则∠BCD 的大小是(B). A.18° B.36° C.54° D.72° 7.已知一个三角形的三边长分别为 5,7,8,则其内切圆的半径为(C). A.√3 2 B.3 2 C.√3 D.2√3

8.如图①,在扇形AOB中,OA=10,∠AOB=36°若固定点B,将此扇形顺时针方向旋 转,得一新扇形A'OB,其中点A在OB上,如图②所示,则点O旋转至点O所经过 的长度为(D) 图① 图② A.元 B.2元 C.3π D.4元 9.若圆锥的底面半径r=3,高h=4,则圆锥的侧面积是(B) A.12π B.15π C.24π D.30元 10.若以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三 角形,则该三角形的面积是(A), A号 B C.√z D.v3 二、填空题(每小题4分,共24分) 11.如图所示,AB是⊙O的直径,弦DC与AB相交于点E,若∠C=50°,则∠DAB=」 40°
8.如图①,在扇形 AOB 中,OA=10,∠AOB=36°.若固定点 B,将此扇形顺时针方向旋 转,得一新扇形 A'O'B, 其中点 A 在 O'B 上,如图②所示,则点 O 旋转至点 O'所经过 的长度为(D). 图① 图② A.π B.2π C.3π D.4π 9.若圆锥的底面半径 r=3,高 h=4,则圆锥的侧面积是(B). A.12π B.15π C.24π D.30π 10.若以半径为 2 的圆的内接正三角形、正方形、正六边形的边心距为三边作三 角形,则该三角形的面积是(A). A.√2 2 B.√3 2 C.√2 D.√3 二、填空题(每小题 4 分,共 24 分) 11.如图所示,AB 是☉O 的直径,弦 DC 与 AB 相交于点 E,若∠C=50°,则∠DAB= 40°
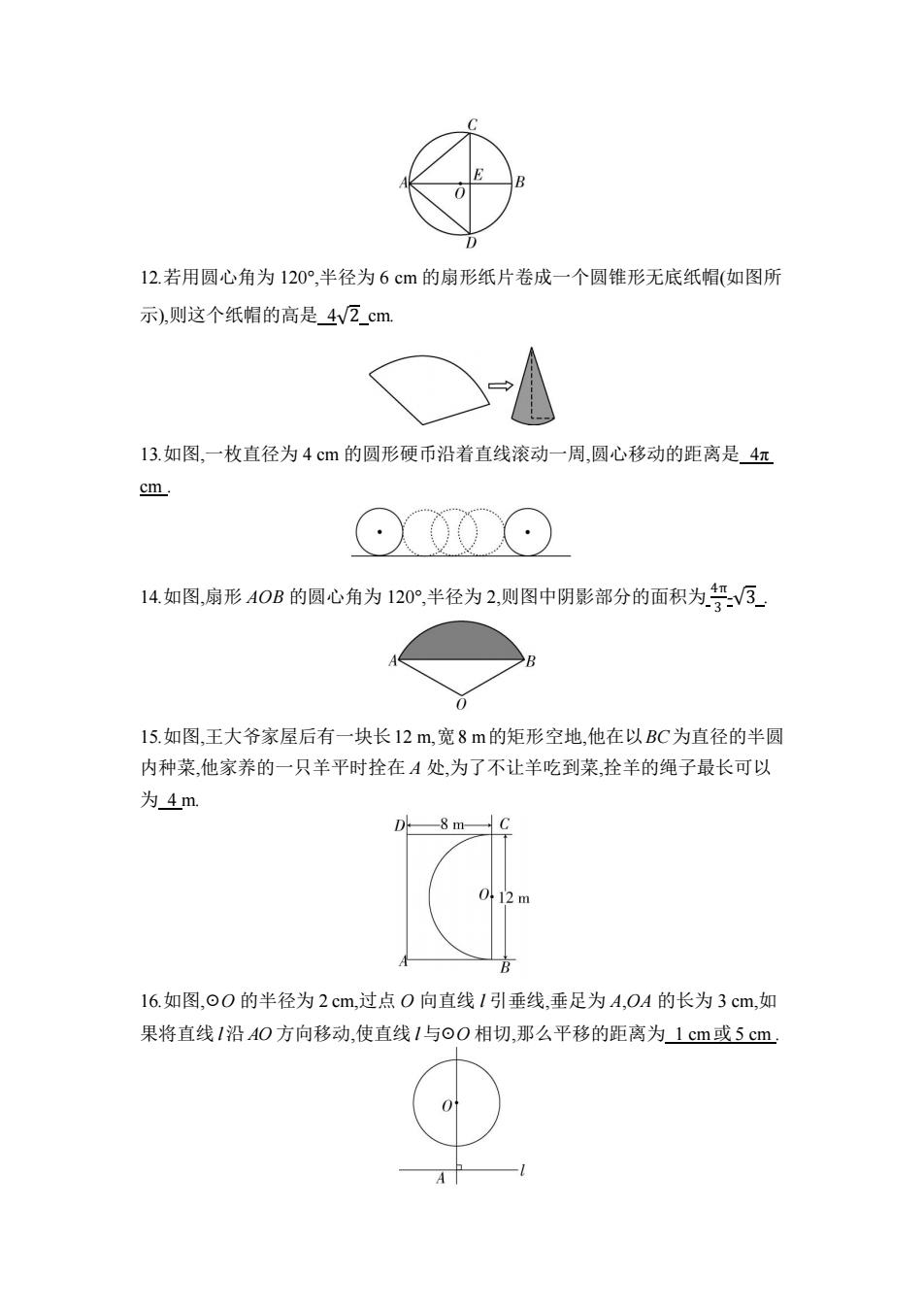
D 12.若用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所 示),则这个纸帽的高是4v2cm 13.如图,一枚直径为4cm的圆形硬币沿着直线滚动一周,圆心移动的距离是4π cm. ⊙00⊙ 14.如图,扇形40B的圆心角为120°,半径为2,则图中阴影部分的面积为号V3 0 15.如图,王大爷家屋后有一块长12m,宽8m的矩形空地,他在以BC为直径的半圆 内种菜,他家养的一只羊平时拴在A处,为了不让羊吃到菜,拴羊的绳子最长可以 为4m 8 m 012m 16.如图,⊙O的半径为2cm,过点O向直线1引垂线,垂足为A,OA的长为3cm,如 果将直线1沿AO方向移动,使直线1与⊙O相切,那么平移的距离为1cm或5cm
12.若用圆心角为 120°,半径为 6 cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所 示),则这个纸帽的高是 4√2 cm. 13.如图,一枚直径为 4 cm 的圆形硬币沿着直线滚动一周,圆心移动的距离是 4π cm . 14.如图,扇形 AOB 的圆心角为 120°,半径为 2,则图中阴影部分的面积为 4π 3 -√3 . 15.如图,王大爷家屋后有一块长12 m,宽8 m的矩形空地,他在以BC为直径的半圆 内种菜,他家养的一只羊平时拴在 A 处,为了不让羊吃到菜,拴羊的绳子最长可以 为 4 m. 16.如图,☉O 的半径为 2 cm,过点 O 向直线 l 引垂线,垂足为 A,OA 的长为 3 cm,如 果将直线 l沿 AO 方向移动,使直线 l与☉O 相切,那么平移的距离为 1 cm或 5 cm

三、解答题(共96分,写出必要的文字说明、证明过程或演算步骤) 17.(8分)如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,求折痕AB 的长 0 解:如图,作OD LAB,垂足为点D,连接OA,根据题意得OD0A=1cm,根据勾股定 理得AD=√3cm,根据垂径定理得AB=2V3cm 18.(8分)如图,在△ABC中,BC=3cm,∠BAC=60°,求能把△ABC覆盖的圆形纸片的 最小半径 0 解:作⊙O的直径CD,连接BD.因为∠A,∠D都是BC所对的圆周角,所以 ∠D=∠A=60°.因为CD是⊙O的直径,所以∠DBC=90°,所以∠DCB=30°,所以 BD-CD. 又BC=3cm,所以在Rt△CDB中,BC2+DB2=DC2,即9+DC2=DC2,解得CD=2V3 所以⊙O的半径是v3cm.所以能把△ABC覆盖的圆形纸片的最小半径为v3cm 19.(10分)如图,AB是⊙O的直径,P为AB延长线上任意一点,C为半圆ACB的中 点,PD切OO于点D,连接CD交AB于点E. 求证:PD=PE 证明:如图,连接OC,则有∠OCD=∠ODC
三、解答题(共 96 分,写出必要的文字说明、证明过程或演算步骤) 17.(8 分)如图,将半径为 2 cm 的圆形纸片折叠后,圆弧恰好经过圆心 O,求折痕 AB 的长. 解:如图,作 OD⊥AB,垂足为点 D,连接 OA,根据题意得OD=1 2 OA=1 cm,根据勾股定 理得 AD=√3 cm,根据垂径定理得 AB=2√3 cm. 18.(8 分)如图,在△ABC 中,BC=3 cm,∠BAC=60°,求能把△ABC 覆盖的圆形纸片的 最小半径. 解:作☉O 的直径 CD,连接 BD.因为∠A,∠D 都是𝐵𝐶⏜ 所对的圆周角,所以 ∠D=∠A=60°.因为 CD 是☉O 的直径,所以∠DBC=90°,所以∠DCB=30°,所以 BD=1 2 CD. 又 BC=3 cm,所以在 Rt△CDB 中,BC2+DB2=DC2 ,即 9+ 1 4 DC2=DC2 ,解得 CD=2√3. 所以☉O 的半径是√3 cm.所以能把△ABC 覆盖的圆形纸片的最小半径为√3 cm. 19.(10 分)如图,AB 是☉O 的直径,P 为 AB 延长线上任意一点,C 为半圆 ACB 的中 点,PD 切☉O 于点 D,连接 CD 交 AB 于点 E. 求证:PD=PE. 证明:如图,连接 OC,则有∠OCD=∠ODC
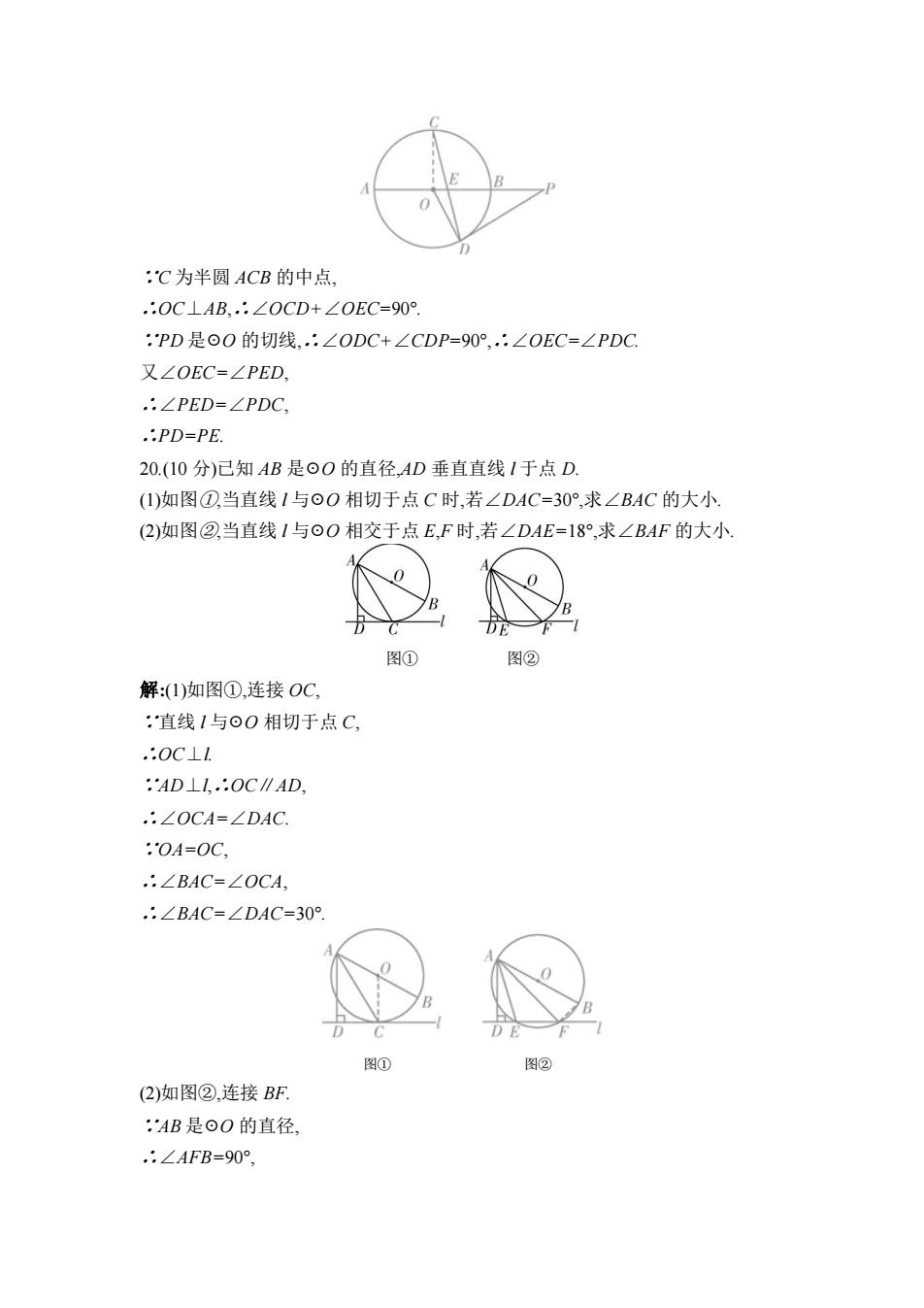
:C为半圆ACB的中点, .:OC⊥AB,:∠OCD+∠OEC=90° :PD是⊙O的切线,:∠ODC+∠CDP=90°,.:∠OEC=∠PDC 又∠OEC=∠PED, .:∠PED=∠PDC, ..PD=PE. 20.(10分)已知AB是⊙O的直径,AD垂直直线1于点D. (1)如图①当直线1与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小 (2)如图②当直线1与⊙O相交于点E,F时,若∠DAE=18°,求∠BAF的大小 图① 图② 解:(1)如图①,连接OC, :直线1与⊙O相切于点C, .:0C⊥1 :AD⊥1,.:OC∥AD .:∠OCA=∠DAC. .OA=OC, .:∠BAC=∠OCA .:∠BAC=∠DAC=30° D E 图① 图② (2)如图②,连接BF. :AB是⊙O的直径 .:∠AFB=90°
∵C 为半圆 ACB 的中点, ∴OC⊥AB,∴∠OCD+∠OEC=90°. ∵PD 是☉O 的切线,∴∠ODC+∠CDP=90°,∴∠OEC=∠PDC. 又∠OEC=∠PED, ∴∠PED=∠PDC, ∴PD=PE. 20.(10 分)已知 AB 是☉O 的直径,AD 垂直直线 l 于点 D. (1)如图①,当直线 l 与☉O 相切于点 C 时,若∠DAC=30°,求∠BAC 的大小. (2)如图②,当直线 l 与☉O 相交于点 E,F 时,若∠DAE=18°,求∠BAF 的大小. 图① 图② 解:(1)如图①,连接 OC, ∵直线 l 与☉O 相切于点 C, ∴OC⊥l. ∵AD⊥l,∴OC∥AD, ∴∠OCA=∠DAC. ∵OA=OC, ∴∠BAC=∠OCA, ∴∠BAC=∠DAC=30°. 图① 图② (2)如图②,连接 BF. ∵AB 是☉O 的直径, ∴∠AFB=90°

.:∠BAF-90°-∠B. 在⊙O中,四边形ABFE是圆的内接四边形 .:∠AEF+∠B=180°. :'∠AEF=∠ADE+∠DAE=90°+18°=108°, .:∠B=180°-108°=72° .:∠BAF=90°-∠B=90°-72°=18° 21.(12分)如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB 上,DE⊥EB (I)求证:AC是△BDE的外接圆的切线, (2)若AD=2√6,AE=6√2,求EC的长 (1)证明:如图,取BD的中点O,连接OE :BE平分∠ABC :∠CBE=∠OBE. 又OB=OE,:∠OBE=∠BEO, .:∠CBE=∠BEO,:BC∥OE. :∠C=90°,:OE⊥AC, :AC是△BDE的外接圆的切线, (2)解:设⊙O的半径为r,则在△AOE中,OA2=OE2+AE2, 即(r+2V62=r2+(6√2, 解得r=2√, ..0A=20E, .:∠A=30°,∠AOE=60° .:∠CBE=∠OBE=30° 又在Rt△DBE中, ∠OBE=30°,BD=4V6,DE=2V6
∴∠BAF=90°-∠B. 在☉O 中,四边形 ABFE 是圆的内接四边形, ∴∠AEF+∠B=180°. ∵∠AEF=∠ADE+∠DAE=90°+18°=108°, ∴∠B=180°-108°=72°, ∴∠BAF=90°-∠B=90°-72°=18°. 21.(12 分)如图,在 Rt△ABC 中,∠C=90°,BE 平分∠ABC 交 AC 于点 E,点 D 在 AB 上,DE⊥EB. (1)求证:AC 是△BDE 的外接圆的切线. (2)若 AD=2 √6,AE=6 √2,求 EC 的长. (1)证明:如图,取 BD 的中点 O,连接 OE. ∵BE 平分∠ABC, ∴∠CBE=∠OBE. 又 OB=OE,∴∠OBE=∠BEO, ∴∠CBE=∠BEO,∴BC∥OE. ∵∠C=90°,∴OE⊥AC, ∴AC 是△BDE 的外接圆的切线. (2)解:设☉O 的半径为 r,则在△AOE 中,OA2=OE2+AE2 , 即(r+2√6) 2=r2+(6√2) 2 , 解得 r=2√6, ∴OA=2OE, ∴∠A=30°,∠AOE=60°. ∴∠CBE=∠OBE=30°. 又在 Rt△DBE 中, ∠OBE=30°,BD=4√6,DE=2√6

.:BE=6V2. :EC=2BE=3×6W2=3V2 22.(12分)如图,在△ABC中,已知BC=AC,以BC为直径的⊙O与边AB相交于点 D,DE⊥AC,垂足为点E. (I)求证D是AB的中点. (2)判断DE与⊙O的位置关系,并说明理由. (1)证明:如图,连接CD, 则CD⊥AB. 又AC=BC,所以AD=BD, 即D是AB的中点 (2)解:DE是⊙O的切线理由如下: 连接OD,则DO是△ABC的中位线, .:DO∥AC 又DE⊥AC, .:DE⊥DO, 即DE是⊙O的切线 23.(12分)如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O 上,CA=CD,∠CDA=30° (1)试判断直线CD与⊙O的位置关系,并说明理由, (2)若⊙O的半径为5,求点A到CD所在直线的距离
∴BE=6√2. ∴EC=1 2 BE=1 2 ×6√2=3√2. 22.(12 分)如图,在△ABC 中,已知 BC=AC,以 BC 为直径的☉O 与边 AB 相交于点 D,DE⊥AC,垂足为点 E. (1)求证:D 是 AB 的中点. (2)判断 DE 与☉O 的位置关系,并说明理由. (1)证明:如图,连接 CD, 则 CD⊥AB. 又 AC=BC,所以 AD=BD, 即 D 是 AB 的中点. (2)解:DE 是☉O 的切线.理由如下: 连接 OD,则 DO 是△ABC 的中位线, ∴DO∥AC. 又 DE⊥AC, ∴DE⊥DO, 即 DE 是☉O 的切线. 23.(12 分)如图,AB 是☉O 的直径,点 D 在 AB 的延长线上,点 C 在☉O 上,CA=CD,∠CDA=30°. (1)试判断直线 CD 与☉O 的位置关系,并说明理由. (2)若☉O 的半径为 5,求点 A 到 CD 所在直线的距离

解:(1)直线CD与⊙O相切 理由::'△ACD是等腰三角形∠CDA=30° .:∠CAD=∠CDA=30° 如图,连接OC,·AO=CO .:△AOC是等腰三角形 .:∠ACO=∠CAO=30° .:∠C0D=60° 又在△COD中,∠CDO=30°, .:∠DC0=90° :CD是⊙O的切线, 即直线CD与⊙O相切. (2)如图,过点A作AE⊥CD,垂足为E 在Rt△COD中,:'∠CDO=30°, ..OD=20C=10AD=AO+OD=15. 在Rt△ADE中,:'∠EDA=30°, :AE=3AD=7.5 24.(12分)如图,在正方形ABCD中,AB=4,O为对角线BD的中点,分别以OB,OD为 直径作⊙01,⊙02. (1)求⊙01的半径 (2)求图中阴影部分的面积 0 解:(1)在正方形ABCD中, AB=AD=4,∠A=90° .:BD=V42+4Z=4VZ 001=4BD-×4V2=V2
解:(1)直线 CD 与☉O 相切. 理由:∵△ACD 是等腰三角形,∠CDA=30°. ∴∠CAD=∠CDA=30°. 如图,连接 OC,∵AO=CO, ∴△AOC 是等腰三角形. ∴∠ACO=∠CAO=30°. ∴∠COD=60°. 又在△COD 中,∠CDO=30°, ∴∠DCO=90°. ∴CD 是☉O 的切线, 即直线 CD 与☉O 相切. (2)如图,过点 A 作 AE⊥CD,垂足为 E. 在 Rt△COD 中,∵∠CDO=30°, ∴OD=2OC=10,AD=AO+OD=15. 在 Rt△ADE 中,∵∠EDA=30°, ∴AE=1 2 AD=7.5. 24.(12 分)如图,在正方形 ABCD 中,AB=4,O 为对角线 BD 的中点,分别以 OB,OD 为 直径作☉O1,☉O2. (1)求☉O1 的半径. (2)求图中阴影部分的面积. 解:(1)在正方形 ABCD 中, AB=AD=4,∠A=90°, ∴BD=√4 2 + 4 2=4√2, ∴OO1= 1 4 BD=1 4 ×4√2=√2

:O1的半径为v2. (2)如图,连接O1E. :BD为正方形ABCD的对角线, :∠AB0=45° .O1E=01B. .:∠BEO1=∠EBO1=45°, ∠E0iB=02=50e0,E50,E-20%2xV②-l 根据图形的对称性得S1=S2=S3=S4, .:S明影=4S1=2π-4. 0 0 B 25.(12分)如图,已知AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点 E,AD⊥CD于点D (I)求证:AE平分∠DAC (2)若AB=3,∠ABE=60°.①求AD的长,②求出图中阴影部分的面积. (1)证明:如图,连接OE. E B :CD是⊙O的切线,:OE⊥CD :AD⊥CD,AD∥OE .:∠DAE=∠AEO.:OA=OE
∴☉O1 的半径为√2. (2)如图,连接 O1E. ∵BD 为正方形 ABCD 的对角线, ∴∠ABO=45°. ∵O1E=O1B, ∴∠BEO1=∠EBO1=45°, ∴∠EO1B=90°,∴S1=𝑆扇形𝑂1𝐵𝐸-𝑆△𝑂1𝐵𝐸= 90×π×(√2) 2 360 - 1 2 ×(√2) 2= 1 2 π-1. 根据图形的对称性得 S1=S2=S3=S4, ∴S 阴影=4S1=2π-4. 25.(12 分)如图,已知 AB 是☉O 的直径,C 是 AB 延长线上一点,CD 与☉O 相切于点 E,AD⊥CD 于点 D. (1)求证:AE 平分∠DAC. (2)若 AB=3,∠ABE=60°.①求 AD 的长;②求出图中阴影部分的面积. (1)证明:如图,连接 OE. ∵CD 是☉O 的切线,∴OE⊥CD. ∵AD⊥CD,∴AD∥OE. ∴∠DAE=∠AEO.∵OA=OE