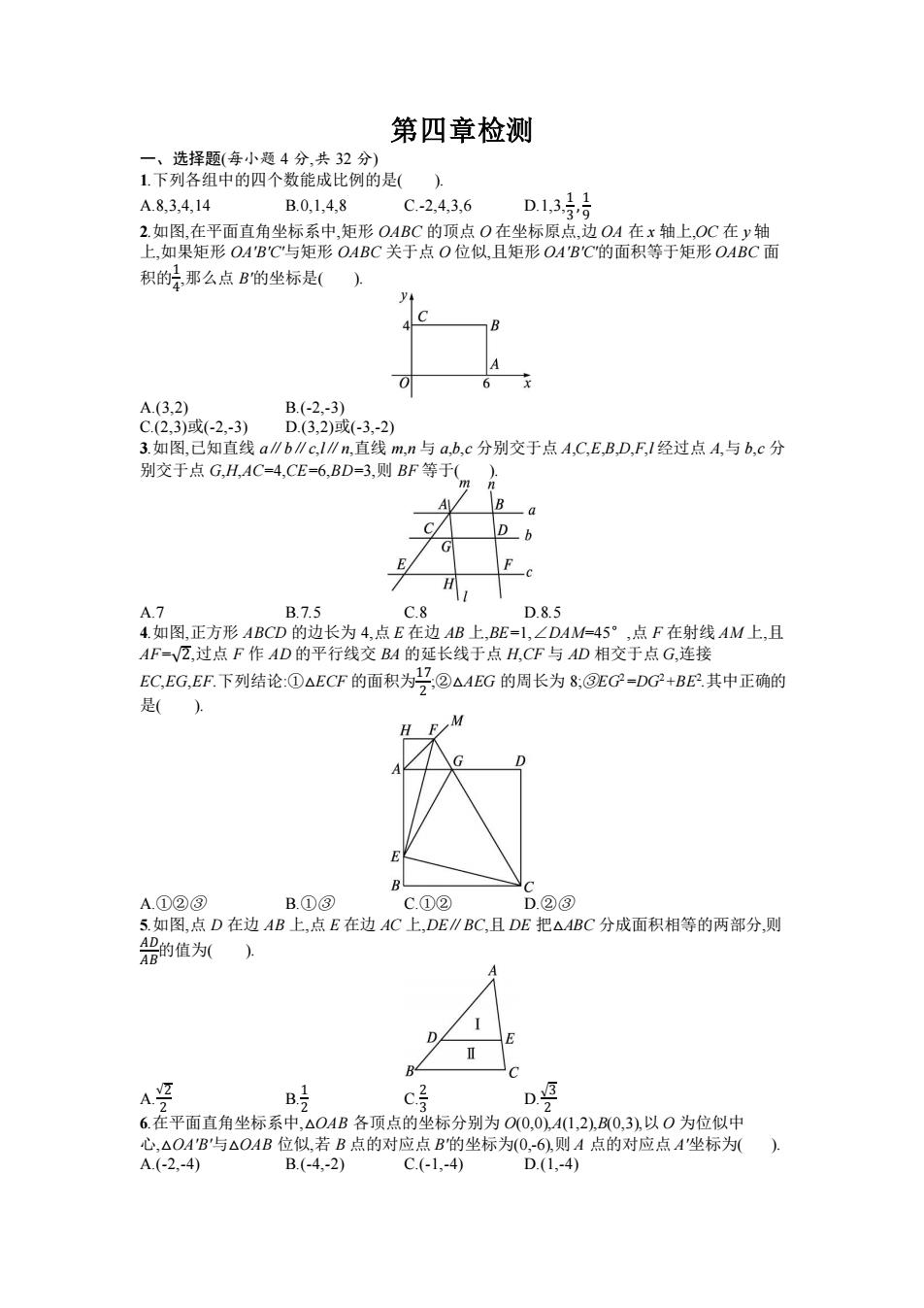
第四章检测 一、选择题(每小题4分,共32分) 1.下列各组中的四个数能成比例的是() A.8,3,4,14 B.0,1,4,8 C.-2,4,3,6 D.1,3号号 2.如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴 上,如果矩形OA'B'C与矩形OABC关于点O位似,且矩形OA'B'C的面积等于矩形OABC面 积的那么点B的坐标是( A.(3,2) B.(-2,-3) C.(2,3)或(-2.-3) D.(3,2)或(-3,-2) 3.如图,已知直线a∥b∥c,I∥n,直线m,n与a,b,c分别交于点A,C,E,B,D,F,I经过点A,与b,c分 别交于点G,H,AC=4,CE=6,BD=3,则BF等于( A B -a D G E H A.7 B.7.5 C.8 D.8.5 4.如图,正方形ABCD的边长为4,点E在边AB上,BE=1,∠DAM=45°,点F在射线AM上,且 AF=VZ,过点F作AD的平行线交BA的延长线于点H,CF与AD相交于点G,连接 EC,EG,EF.下列结论①△ECF的面积为号,2△ABG的周长为8,③EC-DC'+BE其中正确的 是() H F M G B C A.①②③ B.①③ C.①② D.②③ 5.如图,点D在边AB上,点E在边AC上,DE∥BC,且DE把△ABC分成面积相等的两部分,则 铝的值) B A竖 B c D 6.在平面直角坐标系中,△OAB各顶点的坐标分别为O(0,0),A(1,2),B0,3),以O为位似中 心,△OA'B与△OAB位似,若B点的对应点B的坐标为(O,-6),则A点的对应点A'坐标为() A.(-2.-4) B.(-4.-2) C.(-1,-4) D.(1.-4)
第四章检测 一、选择题(每小题 4 分,共 32 分) 1.下列各组中的四个数能成比例的是( ). A.8,3,4,14 B.0,1,4,8 C.-2,4,3,6 D.1,3,1 3 , 1 9 2.如图,在平面直角坐标系中,矩形 OABC 的顶点 O 在坐标原点,边 OA 在 x 轴上,OC 在 y 轴 上,如果矩形 OA'B'C'与矩形 OABC 关于点 O 位似,且矩形 OA'B'C'的面积等于矩形 OABC 面 积的1 4 ,那么点 B'的坐标是( ). A.(3,2) B.(-2,-3) C.(2,3)或(-2,-3) D.(3,2)或(-3,-2) 3.如图,已知直线 a∥b∥c,l∥n,直线 m,n 与 a,b,c 分别交于点 A,C,E,B,D,F,l 经过点 A,与 b,c 分 别交于点 G,H,AC=4,CE=6,BD=3,则 BF 等于( ). A.7 B.7.5 C.8 D.8.5 4.如图,正方形 ABCD 的边长为 4,点 E 在边 AB 上,BE=1,∠DAM=45°,点 F 在射线 AM 上,且 AF=√2,过点 F 作 AD 的平行线交 BA 的延长线于点 H,CF 与 AD 相交于点 G,连接 EC,EG,EF.下列结论:①△ECF 的面积为17 2 ;②△AEG 的周长为 8;③EG2=DG2+BE2 .其中正确的 是( ). A.①②③ B.①③ C.①② D.②③ 5.如图,点 D 在边 AB 上,点 E 在边 AC 上,DE∥BC,且 DE 把△ABC 分成面积相等的两部分,则 𝐴𝐷 𝐴𝐵的值为( ). A. √2 2 B. 1 2 C. 2 3 D. √3 2 6.在平面直角坐标系中,△OAB 各顶点的坐标分别为 O(0,0),A(1,2),B(0,3),以 O 为位似中 心,△OA'B'与△OAB 位似,若 B 点的对应点 B'的坐标为(0,-6),则 A 点的对应点 A'坐标为( ). A.(-2,-4) B.(-4,-2) C.(-1,-4) D.(1,-4)
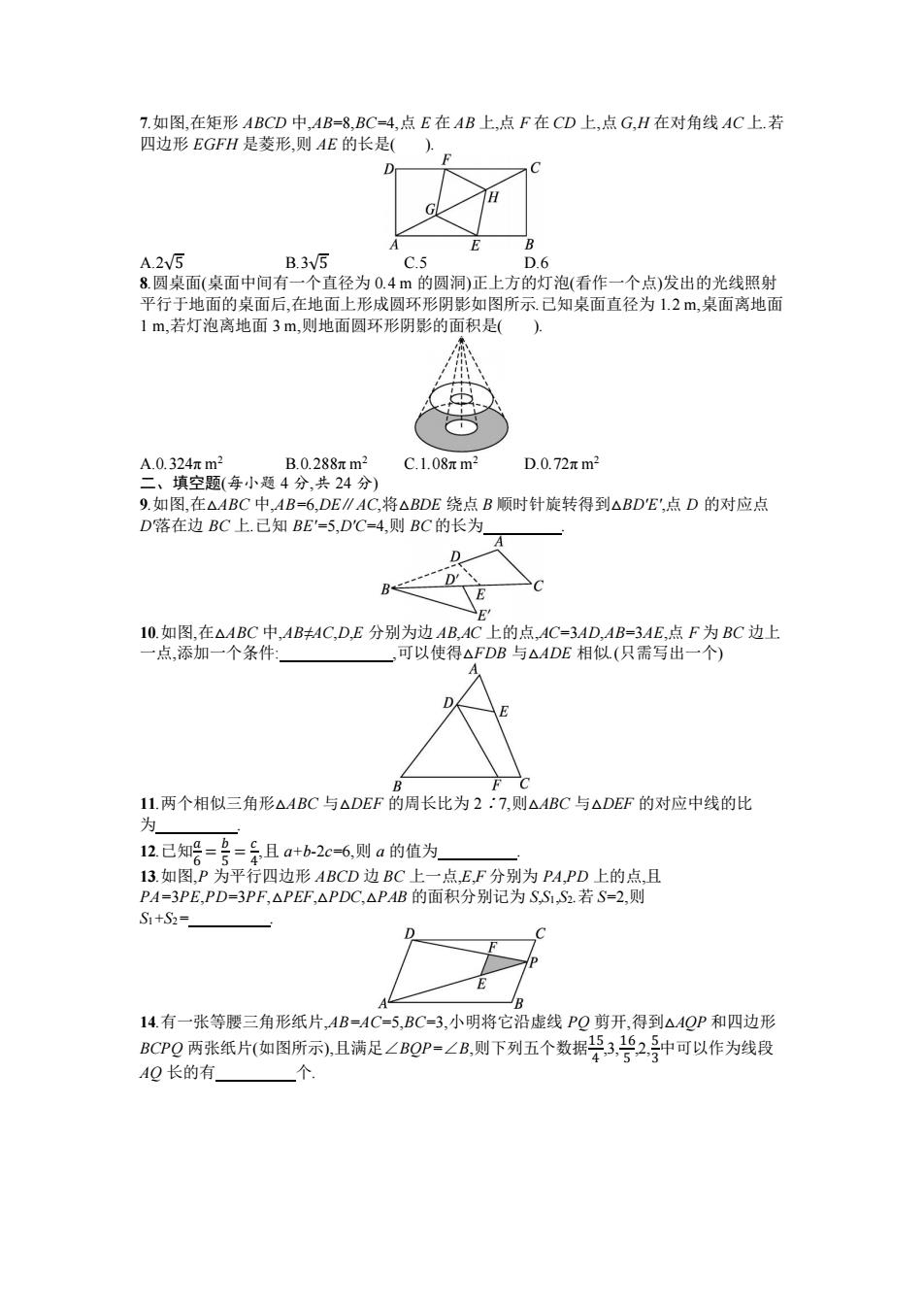
7.如图,在矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上.若 四边形EGFH是菱形,则AE的长是( E A.2V5 B.3v5 C.5 D.6 8.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射 平行于地面的桌面后,在地面上形成圆环形阴影如图所示.己知桌面直径为1.2m,桌面离地面 1m,若灯泡离地面3m,则地面圆环形阴影的面积是(). A.0.324πm2 B.0.288元m2 C.1.08πm2 D.0.72πm2 二、填空题(每小题4分,共24分) 9.如图,在△ABC中,AB=6,DE∥AC,将△BDE绕点B顺时针旋转得到△BDE',点D的对应点 D落在边BC上.已知BE'=5,DC=4,则BC的长为 D D' E 10.如图,在△ABC中,AB≠4C,D,E分别为边AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上 一点,添加一个条件: _,可以使得△FDB与△ADE相似(只需写出一个) 11.两个相似三角形△ABC与△DEF的周长比为2:7,则△ABC与△DEF的对应中线的比 为 12已知号=号=斧且a+b-2c-6,则a的值为 13.如图,P为平行四边形ABCD边BC上一点,E,F分别为PA,PD上的点,且 PA=3PE,PD=3PF,△PEF,△PDC,△PAB的面积分别记为S,S,S.若S-2,则 S1+S2= 14.有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形 BCPO两张纸片(如图所示),且满足∠BQP-∠B,则下列五个数据学3,号兰2中可以作为线段 AQ长的有」 个
7.如图,在矩形 ABCD 中,AB=8,BC=4,点 E 在 AB 上,点 F 在 CD 上,点 G,H 在对角线 AC 上.若 四边形 EGFH 是菱形,则 AE 的长是( ). A.2√5 B.3√5 C.5 D.6 8.圆桌面(桌面中间有一个直径为 0.4 m 的圆洞)正上方的灯泡(看作一个点)发出的光线照射 平行于地面的桌面后,在地面上形成圆环形阴影如图所示.已知桌面直径为 1.2 m,桌面离地面 1 m,若灯泡离地面 3 m,则地面圆环形阴影的面积是( ). A.0.324π m2 B.0.288π m2 C.1.08π m2 D.0.72π m2 二、填空题(每小题 4 分,共 24 分) 9.如图,在△ABC 中,AB=6,DE∥AC,将△BDE 绕点 B 顺时针旋转得到△BD'E',点 D 的对应点 D'落在边 BC 上.已知 BE'=5,D'C=4,则 BC 的长为 . 10.如图,在△ABC 中,AB≠AC,D,E 分别为边 AB,AC 上的点,AC=3AD,AB=3AE,点 F 为 BC 边上 一点,添加一个条件: ,可以使得△FDB 与△ADE 相似.(只需写出一个) 11.两个相似三角形△ABC 与△DEF 的周长比为 2∶7,则△ABC 与△DEF 的对应中线的比 为 . 12.已知𝑎 6 = 𝑏 5 = 𝑐 4 ,且 a+b-2c=6,则 a 的值为 . 13.如图,P 为平行四边形 ABCD 边 BC 上一点,E,F 分别为 PA,PD 上的点,且 PA=3PE,PD=3PF,△PEF,△PDC,△PAB 的面积分别记为 S,S1,S2.若 S=2,则 S1+S2= . 14.有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线 PQ 剪开,得到△AQP 和四边形 BCPQ 两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据15 4 ,3,16 5 ,2,5 3 中可以作为线段 AQ 长的有 个

B 三、解答题(共44分) 15.(6分)如图,△4BC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将 △ABC放大为原来的2倍得到△A'B'C 87 6 2 ---十--- 012345678x (I)在图中第一象限内画出符合要求的△4'B'C,(不要求写画法) (2)△4'B'C的面积是 16.(8分)如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延 长线于点E,交AC于点F A DM 求证:(I)AE=AF: (2)BE-AB+AC). 17.(10分)如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B 处,恰好在镜子中看到楼的顶部E,再将镜子放到C处,然后后退到D处,恰好再次在镜子中看 到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC-=2m,BD=2.1m,如果小明眼晴距地面高 度BF,DG为1.6m,试确定楼的高度OE
三、解答题(共 44 分) 15.(6 分)如图,△ABC 三个顶点的坐标分别为 A(1,2),B(3,1),C(2,3),以原点 O 为位似中心,将 △ABC 放大为原来的 2 倍得到△A'B'C'. (1)在图中第一象限内画出符合要求的△A'B'C';(不要求写画法) (2)△A'B'C'的面积是 . 16.(8 分)如图,已知△ABC,AD 平分∠BAC 交 BC 于点 D,BC 的中点为 M,ME∥AD,交 BA 的延 长线于点 E,交 AC 于点 F. 求证:(1)AE=AF; (2)BE=1 2 (AB+AC). 17.(10 分)如图,为了测量一栋楼的高度 OE,小明同学先在操场上 A 处放一面镜子,向后退到 B 处,恰好在镜子中看到楼的顶部 E;再将镜子放到 C 处,然后后退到 D 处,恰好再次在镜子中看 到楼的顶部 E(O,A,B,C,D 在同一条直线上),测得 AC=2 m,BD=2.1 m,如果小明眼睛距地面高 度 BF,DG 为 1.6 m,试确定楼的高度 OE
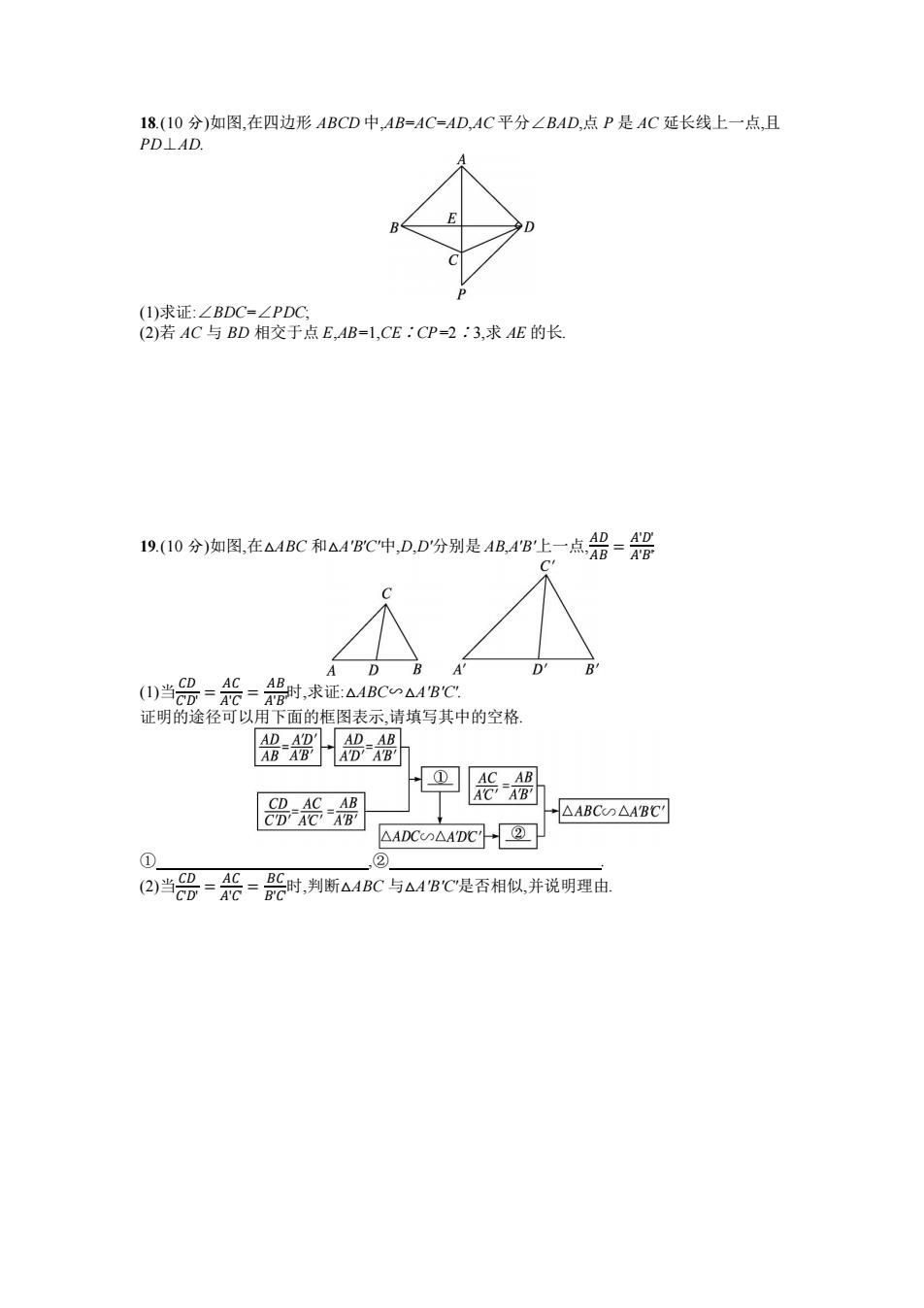
18.(10分)如图,在四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且 PD⊥AD. (I)求证:∠BDC=∠PDC, (2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长 I9(I0分)陶图,在A1BC和△MBC中D,D'分别是ABAB上一点,铝-铝 A D A D ()当品=怨=0时,求证△ABCAB 证明的途径可以用下面的框图表示,请填写其中的空格. AD A'D' AD AB AB AB' AD'AB' ① AC AB AC'AB CD_AC AB △ABCD△ABC' CD'AC'AB △ADCC∽△ADC' ② ① ② ②)当号=荒=二时,判断A1BC与△1BC是否相似并说明理由 AC
18.(10 分)如图,在四边形 ABCD 中,AB=AC=AD,AC 平分∠BAD,点 P 是 AC 延长线上一点,且 PD⊥AD. (1)求证:∠BDC=∠PDC; (2)若 AC 与 BD 相交于点 E,AB=1,CE∶CP=2∶3,求 AE 的长. 19.(10 分)如图,在△ABC 和△A'B'C'中,D,D'分别是 AB,A'B'上一点, 𝐴𝐷 𝐴𝐵 = 𝐴'𝐷' 𝐴'𝐵' . (1)当 𝐶𝐷 𝐶'𝐷' = 𝐴𝐶 𝐴'𝐶' = 𝐴𝐵 𝐴'𝐵'时,求证:△ABC∽△A'B'C'. 证明的途径可以用下面的框图表示,请填写其中的空格. ① ,② . (2)当 𝐶𝐷 𝐶'𝐷' = 𝐴𝐶 𝐴'𝐶' = 𝐵𝐶 𝐵'𝐶'时,判断△ABC 与△A'B'C'是否相似,并说明理由

第四章检测 一、选择题 1.D2.D3.B4.C5.A6.A7.C8.D 二、填空题 9.2+V34 1O.(条件不唯一)∠A=∠BDF一或∠A=∠BFD,∠ADE=∠BFD,∠ADE=∠BDF,DF∥ 4c器=器器=器-) 11.2712.1213.1814.3 三、解答题 y 8 15.解(1)012345678x (2)6 16.证明(1)·DA平分∠BAC,.:∠BAD=∠CAD ·AD∥EM, .:∠BAD=∠AEF,∠CAD=∠AFE .:∠AEF=∠AFE,.AE=AF DM (2)过点C作CG∥EM,交BA的延长线于点G :EF∥CG.:∠G=∠AEF,∠ACG=∠AFE. :∠AEF=∠AFE, .:∠G=∠ACG. .AG=AC. .'BM=CM.EM//CG,..BE=EG .:BE-BG-(BA+AG)-(AB+AC). 17.解设OE=xm,AO=am,BC=bm 由AGDC∽AEOC得S=2 0E 即兰=整理得,32+160-21x 由AFB1AE01得,器-8 即=2地,整理得,1.6a=2x-bx 故3.2+2x-bx=2.1x-br,解得x=32 故楼的高度OE为32m. 18.(1)证明:AB=AD,AC平分∠BAD .:AC⊥BD..:∠ACD+∠BDC=90° :AC=AD,:∠ACD=∠ADC :PD⊥AD,.:∠ADC+∠PDC=90°, .:∠BDC=∠PDC
第四章检测 一、选择题 1.D 2.D 3.B 4.C 5.A 6.A 7.C 8.D 二、填空题 9.2+√34 10.(条件不唯一)∠A=∠BDF( 或∠A=∠BFD,∠ADE=∠BFD,∠ADE=∠BDF,DF∥ AC, 𝐵𝐷 𝐴𝐸 = 𝐵𝐹 𝐸𝐷 , 𝐵𝐷 𝐷𝐸 = 𝐵𝐹 𝐴𝐸 ) 11.2∶7 12.12 13.18 14.3 三、解答题 15.解 (1) (2)6 16.证明 (1)∵DA 平分∠BAC,∴∠BAD=∠CAD. ∵AD∥EM, ∴∠BAD=∠AEF,∠CAD=∠AFE. ∴∠AEF=∠AFE,∴AE=AF. (2)过点 C 作 CG∥EM,交 BA 的延长线于点 G. ∵EF∥CG,∴∠G=∠AEF,∠ACG=∠AFE. ∵∠AEF=∠AFE, ∴∠G=∠ACG. ∴AG=AC. ∵BM=CM,EM∥CG,∴BE=EG. ∴BE=1 2 BG=1 2 (BA+AG)= 1 2 (AB+AC). 17.解 设 OE=x m,AO=a m,BC=b m. 由△GDC∽△EOC 得, 𝐷𝐺 𝑂𝐸 = 𝐶𝐷 𝐶𝑂 , 即 1.6 𝑥 = 2.1-𝑏 2+𝑎 ,整理得,3.2+1.6a=2.1x-bx. 由△FBA∽△EOA 得, 𝐵𝐹 𝑂𝐸 = 𝐴𝐵 𝐴𝑂 , 即 1.6 𝑥 = 2-𝑏 𝑎 ,整理得,1.6a=2x-bx. 故 3.2+2x-bx=2.1x-bx,解得 x=32. 故楼的高度 OE 为 32 m. 18.(1)证明 ∵AB=AD,AC 平分∠BAD, ∴AC⊥BD.∴∠ACD+∠BDC=90°. ∵AC=AD,∴∠ACD=∠ADC. ∵PD⊥AD,∴∠ADC+∠PDC=90°, ∴∠BDC=∠PDC

(2)解过点C作CM⊥PD于点M :'∠BDC=∠PDC, ..CE=CM. :‘∠CMP=∠ADP=90°,∠P=∠P, .:△CPM∽AAPD, ..CM=PC AD PA 设CM=CE=x, CE CP-2:3..PC 4B=4D-AC-1 = x+1 解得xA5-1日=号 19.(1证明:40=4D:40 AB 说能 AB CDAC A'D .:△ADC∽△A'DC',.:∠A=∠A :荒=得:C1B℃ 故等案为品号=长=品②∠A∠4 (2)解结论::△ABC∽△A'B'C! 理由:如图,过,点D,D分别作DE∥BC,DE'∥BC',DE交AC于点E,DE交A'C'于点E: E :DE∥BC,.:△ADE∽△ABC, E = = 同理0二p2 C AC AE AB BC :A .:0e DE A'B B'C BC DE= 同理4E :c罪 E 公 g A A'C ..CD AC BC ECP .:△DCE∽△D'CE .:∠CED=∠CE'DI :DE∥BC,:∠CED+∠ACB=18O°, 同理,∠CED+∠A'CB'=180°
(2)解 过点 C 作 CM⊥PD 于点 M. ∵∠BDC=∠PDC, ∴CE=CM. ∵∠CMP=∠ADP=90°,∠P=∠P, ∴△CPM∽△APD, ∴ 𝐶𝑀 𝐴𝐷 = 𝑃𝐶 𝑃𝐴 . 设 CM=CE=x, ∵CE∶CP=2∶3,∴PC=3 2 x. ∵AB=AD=AC=1,∴ 𝑥 1 = 3 2 𝑥 3 2 𝑥+1 , 解得 x= 1 3 .∴AE=1- 1 3 = 2 3 . 19.(1)证明 ∵ 𝐴𝐷 𝐴𝐵 = 𝐴'𝐷' 𝐴'𝐵' ,∴ 𝐴𝐷 𝐴'𝐷' = 𝐴𝐵 𝐴'𝐵' . ∵ 𝐶𝐷 𝐶'𝐷' = 𝐴𝐶 𝐴'𝐶' = 𝐴𝐵 𝐴'𝐵' ,∴ 𝐶𝐷 𝐶'𝐷' = 𝐴𝐶 𝐴'𝐶' = 𝐴𝐷 𝐴'𝐷' , ∴△ADC∽△A'D'C',∴∠A=∠A'. ∵ 𝐴𝐶 𝐴'𝐶' = 𝐴𝐵 𝐴'𝐵' ,∴△ABC∽△A'B'C'. 故答案为① 𝐶𝐷 𝐶'𝐷' = 𝐴𝐶 𝐴'𝐶' = 𝐴𝐷 𝐴'𝐷' ,②∠A=∠A'. (2)解 结论:∴△ABC∽△A'B'C'. 理由:如图,过点 D,D'分别作 DE∥BC,D'E'∥B'C',DE 交 AC 于点 E,D'E'交 A'C'于点 E'. ∵DE∥BC,∴△ADE∽△ABC, ∴ 𝐴𝐷 𝐴𝐵 = 𝐷𝐸 𝐵𝐶 = 𝐴𝐸 𝐴𝐶 . 同理, 𝐴'𝐷' 𝐴'𝐵' = 𝐷'𝐸' 𝐵'𝐶' = 𝐴'𝐸' 𝐴'𝐶' , ∵ 𝐴𝐷 𝐴𝐵 = 𝐴'𝐷' 𝐴'𝐵' ,∴ 𝐷𝐸 𝐵𝐶 = 𝐷'𝐸' 𝐵'𝐶' , ∴ 𝐷𝐸 𝐷'𝐸' = 𝐵𝐶 𝐵'𝐶' . 同理, 𝐴𝐸 𝐴𝐶 = 𝐴'𝐸' 𝐴'𝐶' , ∴ 𝐴𝐶-𝐴𝐸 𝐴𝐶 = 𝐴'𝐶'-𝐴'𝐸' 𝐴'𝐶' , 即 𝐸𝐶 𝐴𝐶 = 𝐸'𝐶' 𝐴'𝐶' ,∴ 𝐸𝐶 𝐸'𝐶' = 𝐴𝐶 𝐴'𝐶' . ∵ 𝐶𝐷 𝐶'𝐷' = 𝐴𝐶 𝐴'𝐶' = 𝐵𝐶 𝐵'𝐶' , ∴ 𝐶𝐷 𝐶'𝐷' = 𝐷𝐸 𝐷'𝐸' = 𝐸𝐶 𝐸'𝐶' , ∴△DCE∽△D'C'E'. ∴∠CED=∠C'E'D'. ∵DE∥BC,∴∠CED+∠ACB=180°, 同理,∠C'E'D'+∠A'C'B'=180°

.:∠ACB=∠A'CB: :光=器ABC1BC
∴∠ACB=∠A'C'B'. ∵ 𝐴𝐶 𝐴'𝐶' = 𝐶𝐵 𝐶'𝐵' ,∴△ABC∽△A'B'C