
第二十三章检测 一、选择题(每小题3分,共30分) 1.下列图形中,既是轴对称图形,又是中心对称图形的是(D) A.平行四边形 B.等边三角形 C.等腰梯形 D.正方形 2.如图,在△ABC中,AC=BC,D,E分别是边AB,AC的中点,若将△ADE绕点E旋转 180得到△CFE,则四边形ADCF一定是(A) A.矩形 B.B菱形 C.正方形 D.D梯形 3.在四边形ABCD中,对角线AC,BD相交于点O,如果AO=CO,BO=DO,AC⊥BD, 那么这个四边形(C)】 A.仅是轴对称图形 B.仅是中心对称图形 C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形也不是中心对称图形 4.下列命题中的真命题是(B) A.全等的两个图形是中心对称图形 B.中心对称的两个图形全等 C.中心对称图形都是轴对称图形 D.轴对称图形都是中心对称图形 5.如图,△ABC是等边三角形,D是边BC的中点,以点D为旋转中心,把△ABC顺时 针旋转60°后得到的图形应是(C)】
第二十三章检测 一、选择题(每小题 3 分,共 30 分) 1.下列图形中,既是轴对称图形,又是中心对称图形的是(D). A.平行四边形 B.等边三角形 C.等腰梯形 D.正方形 2.如图,在△ABC 中,AC=BC,D,E 分别是边 AB,AC 的中点,若将△ADE 绕点 E 旋转 180°得到△CFE,则四边形 ADCF 一定是(A). A. 矩形 B. B.菱形 C. 正方形 D. D.梯形 3.在四边形 ABCD 中,对角线 AC,BD 相交于点 O,如果 AO=CO,BO=DO,AC⊥BD, 那么这个四边形(C). A.仅是轴对称图形 B.仅是中心对称图形 C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形也不是中心对称图形 4.下列命题中的真命题是(B). A.全等的两个图形是中心对称图形 B.中心对称的两个图形全等 C.中心对称图形都是轴对称图形 D.轴对称图形都是中心对称图形 5.如图,△ABC 是等边三角形,D 是边 BC 的中点,以点 D 为旋转中心,把△ABC 顺时 针旋转 60°后得到的图形应是(C)
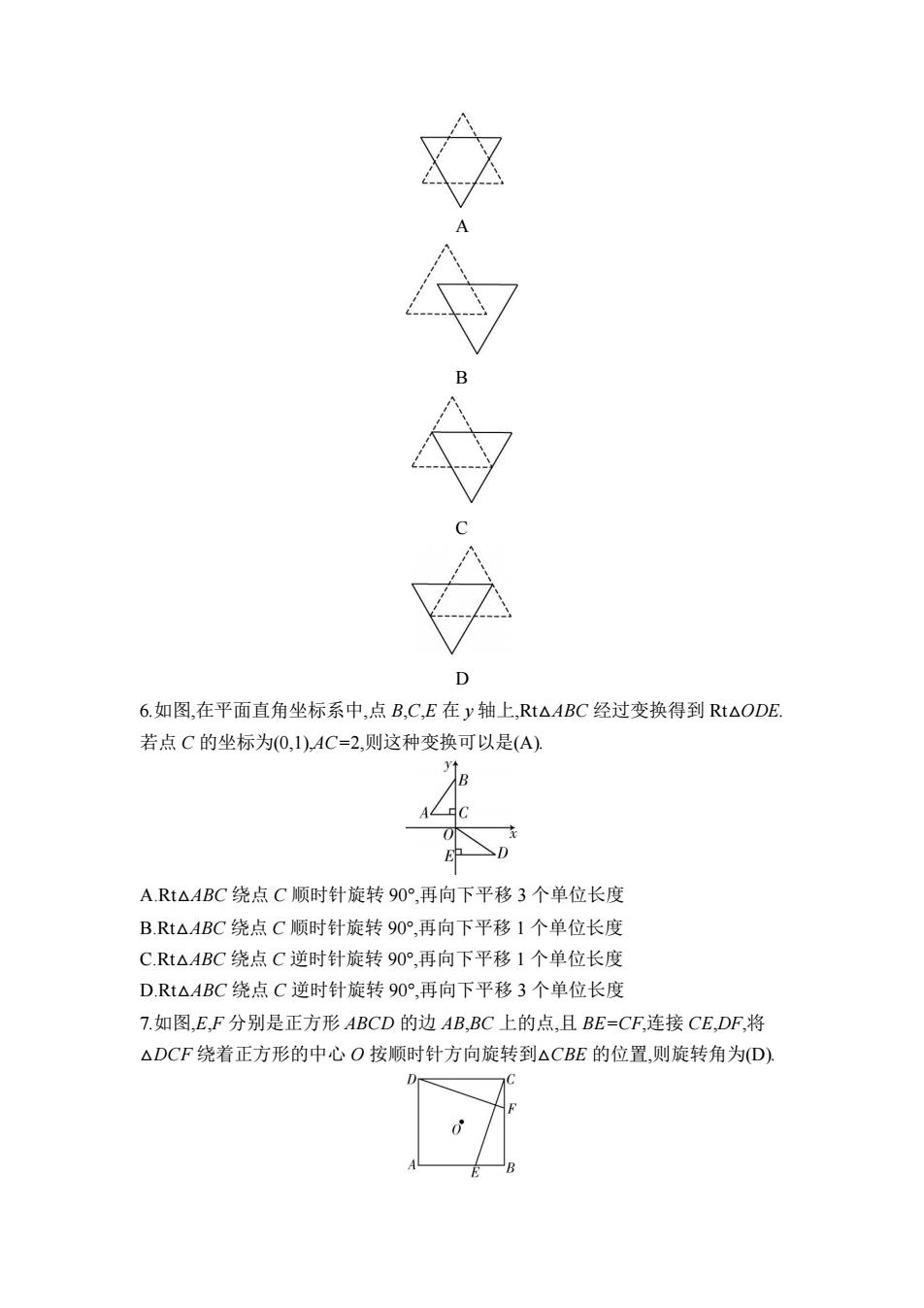
0 6.如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE. 若点C的坐标为0,1),AC=2,则这种变换可以是(A)】 A.Rt△ABC绕点C顺时针旋转90°,再向下平移3个单位长度 B.Rt△ABC绕点C顺时针旋转90°,再向下平移1个单位长度 C.Rt△ABC绕点C逆时针旋转90°,再向下平移1个单位长度 D.Rt△ABC绕点C逆时针旋转90°,再向下平移3个单位长度 7.如图,E,F分别是正方形ABCD的边AB,BC上的点,且BE=CF,连接CE,DF,将 △DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为D)】
A B C D 6.如图,在平面直角坐标系中,点 B,C,E 在 y 轴上,Rt△ABC 经过变换得到 Rt△ODE. 若点 C 的坐标为(0,1),AC=2,则这种变换可以是(A). A.Rt△ABC 绕点 C 顺时针旋转 90°,再向下平移 3 个单位长度 B.Rt△ABC 绕点 C 顺时针旋转 90°,再向下平移 1 个单位长度 C.Rt△ABC 绕点 C 逆时针旋转 90°,再向下平移 1 个单位长度 D.Rt△ABC 绕点 C 逆时针旋转 90°,再向下平移 3 个单位长度 7.如图,E,F 分别是正方形 ABCD 的边 AB,BC 上的点,且 BE=CF,连接 CE,DF,将 △DCF 绕着正方形的中心 O 按顺时针方向旋转到△CBE 的位置,则旋转角为(D)

A.30° B.45° C.60° D.90° 8.在平面直角坐标系中,点A的坐标为(3,4),若将OA绕原点O逆时针旋转90°得到 OA,则点A的坐标是(A) A.(-4,3) B.(-3,4) C.(3,-4) D.(4,-3) 9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是 一个以格点为顶点的正方形(简称格点正方形)若再作一个格点正方形,并涂上阴 影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对 称图形,则这个格点正方形的作法共有(C) A.2种 B.3种 C.4种 D.5种 1O.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点恰好落在边AB 的延长线上的点E处,连接AD.下列结论一定正确的是(C) D A.∠ABD=∠E B.∠CBE=∠C C.ADI∥BC D.AD=BC 二、填空题(每小题4分,共24分) 11.如图所示,在方格纸中,把△ABC绕点A逆时针旋转90度后可得△ABC
A.30° B.45° C.60° D.90° 8.在平面直角坐标系中,点 A 的坐标为(3,4),若将 OA 绕原点 O 逆时针旋转 90°得到 OA',则点 A'的坐标是(A). A.(-4,3) B.(-3,4) C.(3,-4) D.(4,-3) 9.如图,在 4×4 的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是 一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴 影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对 称图形,则这个格点正方形的作法共有(C). A.2 种 B.3 种 C.4 种 D.5 种 10.如图,将△ABC 绕点 B 顺时针旋转 60°得△DBE,点 C 的对应点恰好落在边 AB 的延长线上的点 E 处,连接 AD.下列结论一定正确的是(C). A.∠ABD=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC 二、填空题(每小题 4 分,共 24 分) 11.如图所示,在方格纸中,把△ABC 绕点 A 逆时针旋转 90 度后可得△A'B'C

1A1 12.如图所示,在等边三角形ABC中,E,D分别为AB,BC上的点,且BE=CD,AD与 CE交于点M,则∠AME的大小为60° 13.△ABC在直角坐标系中如图所示,将△ABC向右平移3个单位长度后得到 △A1B1C1,再将△A1B1C绕点O旋转180°后得到△A2B2C2 甲同学说:A1的坐标为3,1)乙同学说:S四边形ABB,4=3.丙同学说:B2C=2W2丁同学 说:∠AC2O=45°.则丁同学的说法正确」 4 -0i23龙 14.正方形绕其中心旋转一定的角度与原图形重合,则这个角至少为90度, 15.如图,点D是等边三角形ABC内一点,如果△ABD绕点A逆时针旋转后能与 △ACE重合,那么△ABD至少旋转了60度 16.如图,直线y=+3与x轴、y轴分别交于A,B两点,把△AOB绕点A旋转90° 后得到△AOB',则点B的坐标是(1-2)或52)
12.如图所示,在等边三角形 ABC 中,E,D 分别为 AB,BC 上的点,且 BE=CD,AD 与 CE 交于点 M,则∠AME 的大小为 60° . 13.△ABC 在直角坐标系中如图所示,将△ABC 向右平移 3 个单位长度后得到 △A1B1C1,再将△A1B1C1绕点 O 旋转 180°后得到△A2B2C2. 甲同学说:A1 的坐标为(3,1).乙同学说:𝑆四边形𝐴𝐵𝐵1𝐴1 =3.丙同学说:B2C=2√2.丁同学 说:∠AC2O=45°.则 丁 同学的说法正确. 14.正方形绕其中心旋转一定的角度与原图形重合,则这个角至少为 90 度. 15.如图,点 D 是等边三角形 ABC 内一点,如果△ABD 绕点 A 逆时针旋转后能与 △ACE 重合,那么△ABD 至少旋转了 60 度. 16.如图,直线 y=- 3 2 x+3 与 x 轴、y 轴分别交于 A,B 两点,把△AOB 绕点 A 旋转 90° 后得到△AO'B',则点 B'的坐标是 (-1,-2)或(5,2)

三、解答题(共96分,写出必要的文字说明、证明过程或演算步骤) 17.(8分)如图,等边三角形ABC经过平移后得到△BDE,其平移的方向为点A到点 B的方向,平移的距离为线段AB的长,△BDE能否看作是△ABC经过旋转得到的? 如果可以,请指出旋转中心,并说出旋转角的大小 解:△BDE能够看作是△ABC按顺时针方向旋转得到的,点B是旋转中心,旋转角 度为120°:或看作是△ABC按逆时针方向旋转得到的,点B是旋转中心,旋转角度 为240° 18.(8分)如图,△ABC为等腰直角三角形,D为AB的中点,AB=2,扇形ADG,BDH的 圆心角∠DAG,∠DBH都等于90°,求阴影部分图形的面积 答案 19.(10分)如图,在平面直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴 的负半轴、y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋 转90°,再把所得的图形沿x轴正方向平移1个单位长度,得△CDO. (1)写出点A,C的坐标 (2)求点A和点C之间的距离. 0 解:(1)点A的坐标是(-2,0),点C的坐标是(1,2), (2)连接AC,在Rt△ACD中, AD=OA+OD=3,CD=2, AC2=CD2+AD2=22+32=13
三、解答题(共 96 分,写出必要的文字说明、证明过程或演算步骤) 17.(8 分)如图,等边三角形 ABC 经过平移后得到△BDE,其平移的方向为点 A 到点 B 的方向,平移的距离为线段 AB 的长,△BDE 能否看作是△ABC 经过旋转得到的? 如果可以,请指出旋转中心,并说出旋转角的大小. 解:△BDE 能够看作是△ABC 按顺时针方向旋转得到的,点 B 是旋转中心,旋转角 度为 120°;或看作是△ABC 按逆时针方向旋转得到的,点 B 是旋转中心,旋转角度 为 240°. 18.(8 分)如图,△ABC 为等腰直角三角形,D 为 AB 的中点,AB=2,扇形 ADG,BDH 的 圆心角∠DAG,∠DBH 都等于 90°,求阴影部分图形的面积. 答案: π−1 2 19.(10 分)如图,在平面直角坐标系中,Rt△AOB 的两条直角边 OA,OB 分别在 x 轴 的负半轴、y 轴的负半轴上,且 OA=2,OB=1.将 Rt△AOB 绕点 O 按顺时针方向旋 转 90°,再把所得的图形沿 x 轴正方向平移 1 个单位长度,得△CDO. (1)写出点 A,C 的坐标. (2)求点 A 和点 C 之间的距离. 解:(1)点 A 的坐标是(-2,0),点 C 的坐标是(1,2). (2)连接 AC,在 Rt△ACD 中, AD=OA+OD=3,CD=2, AC2=CD2+AD2=2 2+3 2=13

即AC=V13 20.(10分)如图,在由边长为1的小正方形组成的网格中,△ABC的顶点均落在格点 上.将△ABC绕点O顺时针旋转90°后,得到△A1B1C1.在网格中画出△A1B1C1. 解:画图如下 B 21.(12分)如图,在Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后再绕点A按 顺时针方向旋转一个角度(a<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F, 直角边DE分别交AB,BC于点G,H. (1)请根据题意用实线补全图形 (2)求证:△AFB≌△AGE. (1)解:画图如下
即 AC=√13. 20.(10 分)如图,在由边长为 1 的小正方形组成的网格中,△ABC 的顶点均落在格点 上.将△ABC 绕点 O 顺时针旋转 90°后,得到△A1B1C1.在网格中画出△A1B1C1. 解:画图如下. 21.(12 分)如图,在 Rt△ABC 中,∠C=90°,将△ABC 沿 AB 向下翻折后,再绕点 A 按 顺时针方向旋转一个角度 α(α<∠BAC),得到 Rt△ADE,其中斜边 AE 交 BC 于点 F, 直角边 DE 分别交 AB,BC 于点 G,H. (1)请根据题意用实线补全图形. (2)求证:△AFB≌△AGE. (1)解:画图如下

B (2)证明:由题意得△ABC≌△AED, .AB=AE,∠ABC=∠E 在△AFB和△AGE中 :'∠ABC=∠EAB=AE,∠FAB=∠GAE, .:AAFB≌△AGE(ASA) 22.(12分)如图,已知△ABC和△A"B"C"及点O. (I)画出△ABC关于点O对称的△ABC! (2)在(1)题的前提下,若△A"B"C"与△A'B'C关于点O对称请确定点O的位置 (3)在(1)题与(2)题的前提下,探究线段OO与线段CC"之间的关系,并说明理由: 答案:(1)(图略) (2)连接CC"和A"A相交于点O (3)00'1Cc"00'-cC" (理由略) 23.(12分)如图,在由边长为1的小正方形组成的方格纸中,有两个全等的三角形 即△A1B1C1和△A2B2C2 (I)请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1重合到△A2B2C2上 (2)在方格纸中将△A1B1C1经过怎样的变换后可以与△A2B2C2成中心对称图形?画 出变换后的三角形并标出对称中心
(2)证明:由题意得△ABC≌△AED, ∴AB=AE,∠ABC=∠E. 在△AFB 和△AGE 中, ∵∠ABC=∠E,AB=AE,∠FAB=∠GAE, ∴△AFB≌△AGE(ASA). 22.(12 分)如图,已知△ABC 和△A″B″C″及点 O. (1)画出△ABC 关于点 O 对称的△A'B'C'. (2)在(1)题的前提下,若△A″B″C″与△A'B'C'关于点 O'对称,请确定点 O'的位置. (3)在(1)题与(2)题的前提下,探究线段 OO'与线段 CC″之间的关系,并说明理由. 答案:(1)(图略) (2)连接 C'C″和 A″A'相交于点 O'. (3)OO'∥CC″,OO'=1 2 CC″. (理由略) 23.(12 分)如图,在由边长为 1 的小正方形组成的方格纸中,有两个全等的三角形, 即△A1B1C1 和△A2B2C2. (1)请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1 重合到△A2B2C2上. (2)在方格纸中将△A1B1C1 经过怎样的变换后可以与△A2B2C2成中心对称图形?画 出变换后的三角形并标出对称中心

解:(1)将△A1B1C向上平移4个单位长度,再向右平移3个单位长度,然后绕点C 顺时针旋转90°.(答案不唯一) (2)将△A1B1C1绕点A1逆时针旋转90°得△A1B3C3,△A1B3C3与△A2B2C2关于A1A2 和B2B3的交点P中心对称.(图略.答案不唯一) 24.(12分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为 A(-2,-1),B(-1,1),C(0,-2) (1)点B关于坐标原点O对称的点的坐标为 (2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C. 答案:(11,-1) (2)作图如下 0 B 25.(12分)如图,在☐ABCD中,AB⊥AC,AB=1,BC=√5,对角线AC,BD相交于点O, 将直线AC绕点O顺时针旋转,分别交BCAD于点E,F (1)求证:当旋转角为90时,四边形ABEF是平行四边形 (2)求证:在旋转过程中,线段AF与EC总保持相等
解:(1)将△A1B1C1 向上平移 4 个单位长度,再向右平移 3 个单位长度,然后绕点 C1 顺时针旋转 90°.(答案不唯一) (2)将△A1B1C1 绕点 A1逆时针旋转 90°得△A1B3C3,△A1B3C3与△A2B2C2关于 A1A2 和 B2B3 的交点 P 中心对称.(图略.答案不唯一) 24.(12 分)如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(-2,-1),B(-1,1),C(0,-2). (1)点 B 关于坐标原点 O 对称的点的坐标为 . (2)将△ABC 绕点 C 顺时针旋转 90°,画出旋转后得到的△A1B1C. 答案:(1)(1,-1) (2)作图如下. 25.(12 分)如图,在▱ABCD 中,AB⊥AC,AB=1,BC= √5,对角线 AC,BD 相交于点 O, 将直线 AC 绕点 O 顺时针旋转,分别交 BC,AD 于点 E,F. (1)求证:当旋转角为 90°时,四边形 ABEF 是平行四边形. (2)求证:在旋转过程中,线段 AF 与 EC 总保持相等

证明:(1)当∠AOF-90时, AB∥EF.:AF∥BE, :四边形ABEF为平行四边形 (2):四边形ABCD为平行四边形, .:AO=CO,∠FAO=∠ECO ∠AOF=∠COE, .:△AOF≌△COE(ASA) ..AF=EC
证明:(1)当∠AOF=90°时, AB∥EF.∵AF∥BE, ∴四边形 ABEF 为平行四边形. (2)∵四边形 ABCD 为平行四边形, ∴AO=CO,∠FAO=∠ECO, ∠AOF=∠COE, ∴△AOF≌△COE(ASA). ∴AF=EC