
家庭值亚 9 弧长及扇形的面积 第1课时 弧长
9 弧长及扇形的面积 第1课时 弧长

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.在半径为R的圆中,n°的圆心角所对的弧长的计算公式为 nπR = 180 温馨提示 1.在孤长公式中,n表示1°的圆心角的倍数,在计算时,n和180 都可以不写单位, 2.若圆心角的单位不全是度,一定要把分和秒全部转化为度, 再进行计算;若题目中没有明确精确度,可以直接用“π”参与 运算。 导航页
导航页 基础自主梳理 1.在半径为R的圆中,n °的圆心角所对的弧长的计算公式为 l= . 温馨提示 1.在弧长公式中,n表示1°的圆心角的倍数,在计算时,n和180 都可以不写单位. 2.若圆心角的单位不全是度,一定要把分和秒全部转化为度, 再进行计算;若题目中没有明确精确度,可以直接用“π”参与 运算. 𝒏𝛑𝑹 𝟏𝟖𝟎
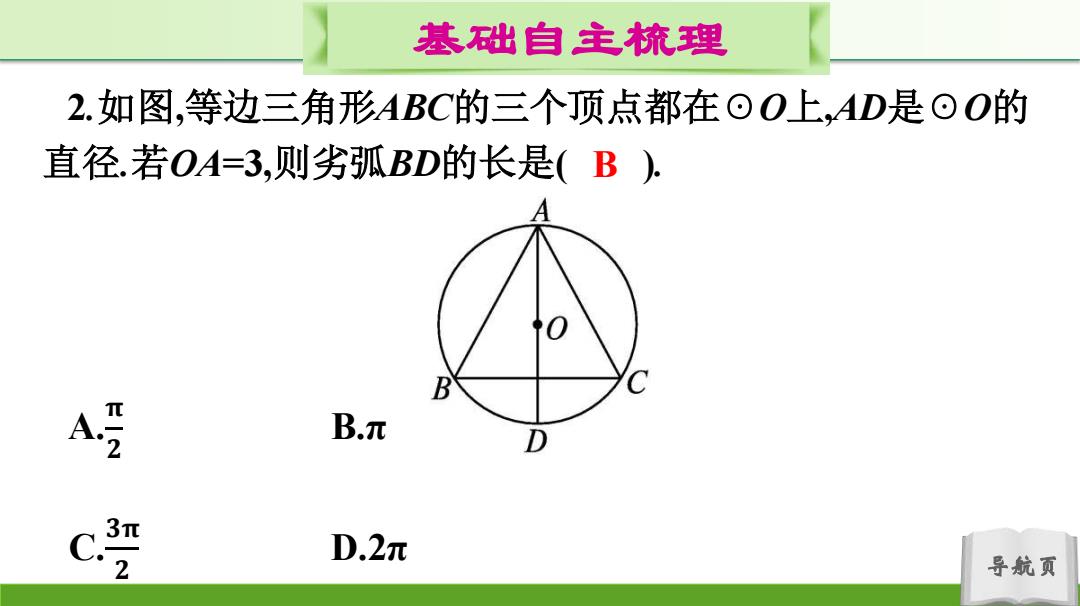
基础自主梳理 2.如图,等边三角形ABC的三个顶点都在⊙O上,AD是⊙O的 直径.若OA=3,则劣弧BD的长是(B). 0 B C 2 B.元 D 3π D.2元 2 导航页
导航页 基础自主梳理 2.如图,等边三角形ABC的三个顶点都在☉O上,AD是☉O的 直径.若OA=3,则劣弧BD的长是( ). A. 𝛑 𝟐 B.π C. 𝟑𝛑 𝟐 D.2π B
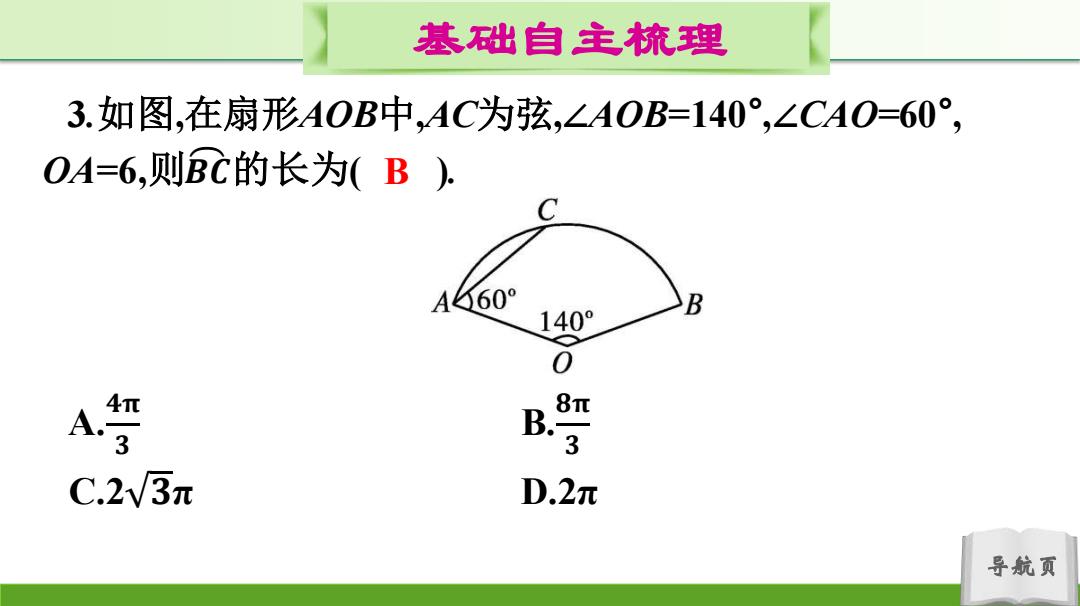
基础自主梳理 3.如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°, OA=6,则BC的长为(B). A60° B 140° 0 4 A T B. C.2y3π D.2π 导航页
导航页 基础自主梳理 3.如图,在扇形AOB中,AC为弦,∠AOB=140° ,∠CAO=60° , OA=6,则 𝑩 𝑪 的长为( ). A. 𝟒𝛑 𝟑 B. 𝟖𝛑 𝟑 C.2 𝟑π D.2π B
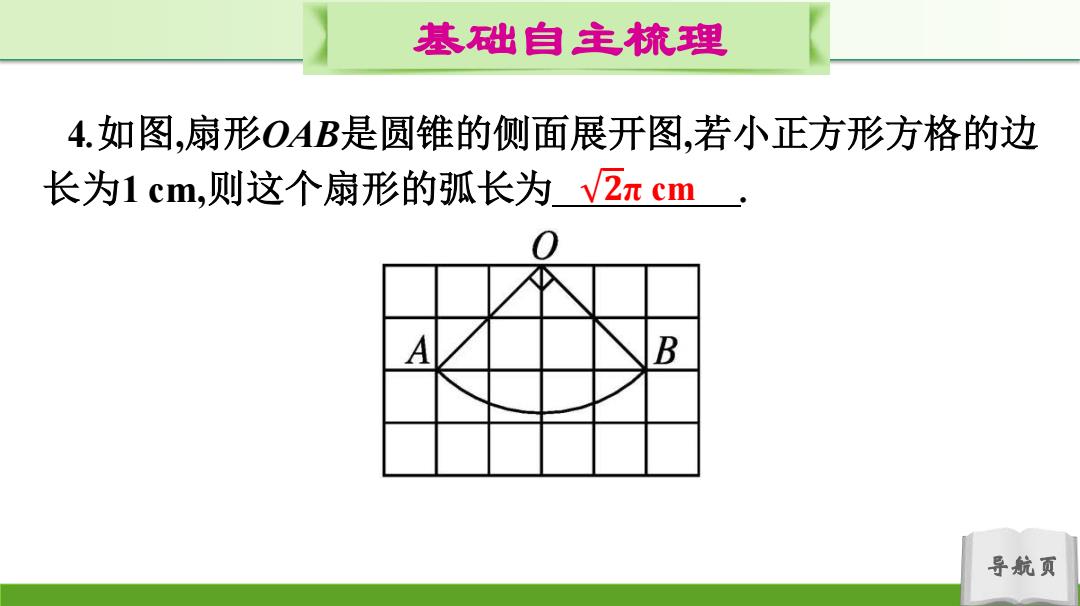
基础自主梳理 4.如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边 长为1cm,则这个扇形的弧长为√2mcm 4 B 导航页
导航页 基础自主梳理 4.如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边 长为1 cm,则这个扇形的弧长为 𝟐π cm

核心重难探究 知识点:弧长 【例题】如图,一段公路的转弯处是一段圆弧(AB),则AB的展直 长度为(B) R=10m 108 A.3元m B.6元m C.9元m D.12元m 思路点拨:求AB的展直长度就是求AB的长,直接利用孤长公式 计算得出答案 导航页
导航页 核心重难探究 知识点:弧长 【例题】 如图,一段公路的转弯处是一段圆弧(𝑨 𝑩),则𝑨 𝑩的展直 长度为( ). A.3π m B.6π m C.9π m D.12π m 思路点拨:求𝑨 𝑩的展直长度就是求𝑨 𝑩的长,直接利用弧长公式 计算得出答案. B
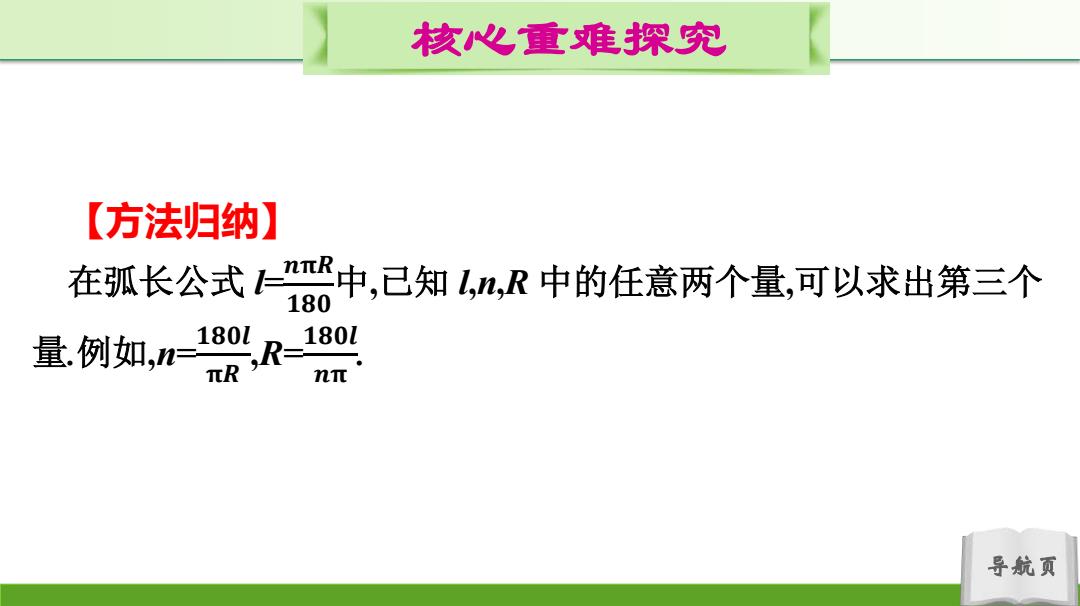
核心重难探究 【方法归纳】 在弧长公式nR中,已知l,n,R中的任意两个量,可以求出第三个 180 量例如,n1股 180L 180L nπ 导航页
导航页 核心重难探究 【方法归纳】 在弧长公式 l=𝒏𝛑𝑹 𝟏𝟖𝟎 中,已知 l,n,R 中的任意两个量,可以求出第三个 量.例如,n= 𝟏𝟖𝟎𝒍 𝛑𝑹 ,R=𝟏𝟖𝟎𝒍 𝒏𝛑
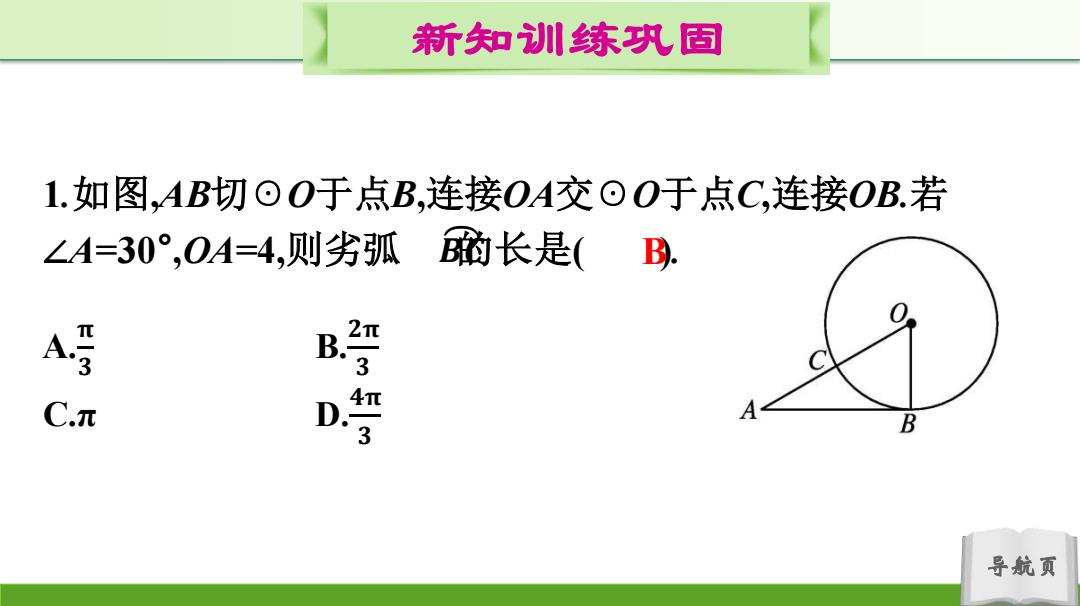
新知训练织固 1.如图,AB切⊙O于点B,连接OA交⊙O于点C,连接OB.若 ∠A=30°,0A=4,则劣弧的长是( B. A写 B 2严 C.元 D 4π A 3 B 导航页
导航页 新知训练巩固 1.如图,AB切☉O于点B,连接OA交☉O于点C,连接OB.若 ∠A=30° ,OA=4,则劣弧 𝑩 的 𝑪 长是( ). A. 𝛑 𝟑 B. 𝟐𝛑 𝟑 C.π D. 𝟒𝛑 𝟑 B
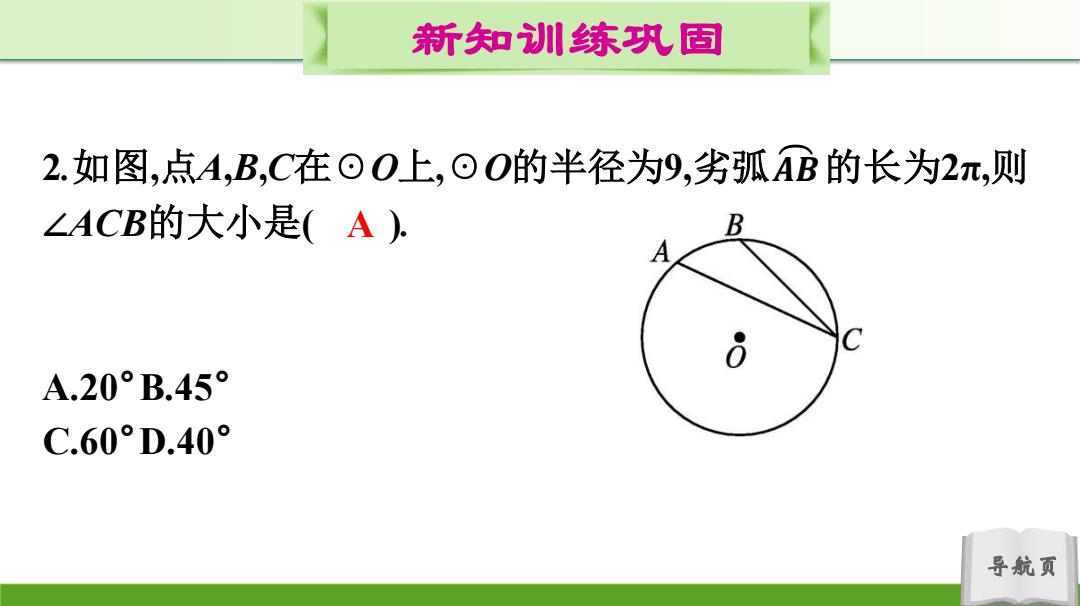
新知训练织固 2.如图,点A,B,C在⊙O上,⊙O的半径为9,劣弧AB的长为2元,则 ∠ACB的大小是(A). A.20°B.45° C.60°D.40° 导航页
导航页 新知训练巩固 2.如图,点A,B,C在☉O上,☉O的半径为9,劣弧 的长为2π,则 ∠ACB的大小是( ). A.20°B.45° C.60°D.40° 𝑨 𝑩 A