
家庭猴四 第三章【 圆 米3垂径定理
第三章 圆 *3 垂径定理

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.垂直于弦的直径平分这条弦,并且平分弦所对 的孤 2.平分弦(不是直径)的直径垂直于弦,并且平分弦所 对的弧 导航页
导航页 基础自主梳理 1.垂直于弦的 平分这条弦,并且平分弦所对 的 . 2.平分弦(不是 )的直径垂直于弦,并且平分弦所 对的 . 直径 弧 直径 弧

基础自主梳理 3.如图,OC为⊙O的半径,OC LAB于点D,已知∠AOC=46°,则 ∠AOB= 92° 4.在⊙O中,弦AB=8,圆心O到AB的距离OC=4,则圆O的半径 长为4v2 B 导航页
导航页 基础自主梳理 3.如图,OC为☉O的半径,OC⊥AB于点D,已知∠AOC=46° ,则 ∠AOB= . 4.在☉O中,弦AB=8,圆心O到AB的距离OC=4,则圆O的半径 长为 . 92° 4 𝟐

核心心重难探究 知识点一:垂径定理及其推论 【例1】如图所示在⊙O中,直径AB垂直于弦CD,垂足为点 E,若BE=2cm,CD=6cm,求⊙O的半径 B 思路点拨:连接OC,由垂径定理可知CE= ;设半径 为r,由 定理可求出r的值 导航页
导航页 核心重难探究 知识点一:垂径定理及其推论 【例1】如图所示,在☉O中,直径AB垂直于弦CD,垂足为点 E,若BE=2 cm,CD=6 cm,求☉O的半径. 思路点拨:连接OC,由垂径定理可知CE= ;设半径 为r,由 定理可求出r的值
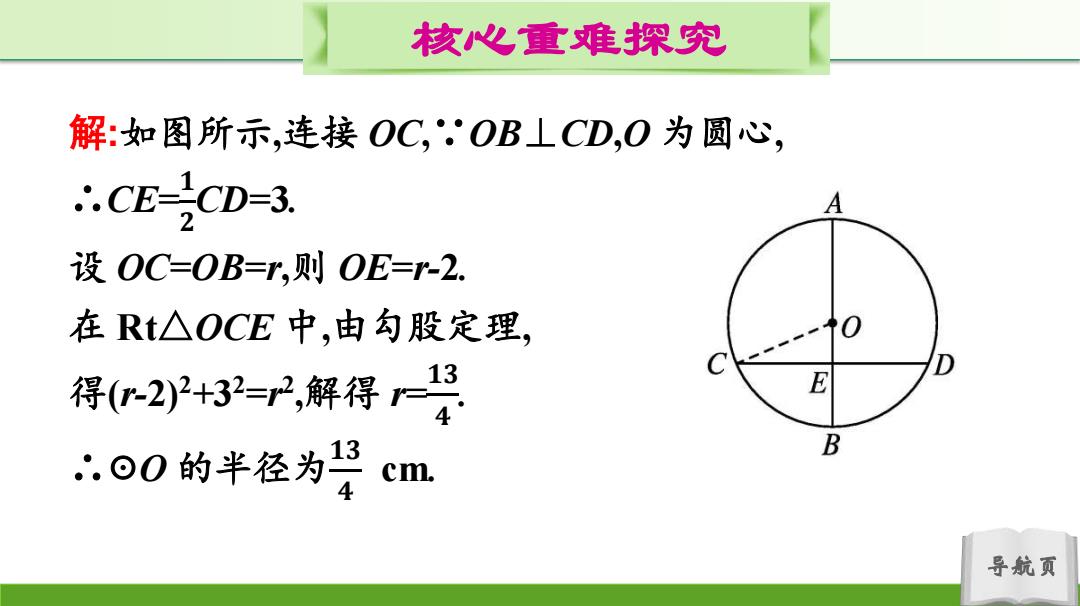
核心重难探究 解:如图所示,连接OC,OB⊥CD,O为圆心, ∴.CE-CD=3. A 2 设OC=OB=r,则OE=r-2. 在Rt△OCE中,由勾股定理, 得2+32=,解得是 D E “⊙0的半径为是 B cm. 导航页
导航页 核心重难探究 解:如图所示,连接 OC,∵OB⊥CD,O 为圆心, ∴CE=𝟏 𝟐 CD=3. 设 OC=OB=r,则 OE=r-2. 在 Rt△OCE 中,由勾股定理, 得(r-2)2 +3 2 =r2 ,解得 r= 𝟏𝟑 𝟒 . ∴☉O 的半径为𝟏𝟑 𝟒 cm

核心重难探究 【方法归纳】 解决与弦有关的问题时,往往需构造以半径、弦心距和弦长 的一半为三边的直角三角形,利用垂径定理和勾股定理求解 即可. 导航页
导航页 核心重难探究 【方法归纳】 解决与弦有关的问题时,往往需构造以半径、弦心距和弦长 的一半为三边的直角三角形,利用垂径定理和勾股定理求解 即可

核心重难探究 知识点二:垂径定理及其推论的应用 免疫区 【例2】为防止禽流感蔓延,某地规定: 捕杀区 0。 离疫点3千米范围内为捕杀区,所有禽类 B 全部捕杀;离疫点3至5千米范围内为免 疫区,所有禽类强制免疫;同时,对捕杀区和免疫区内的村庄、 道路实行全封闭管理现有一条笔直的公路AB通过禽流感病 区,如图,O为疫点,在捕杀区内的公路CD长为4千米,问这条公 路在该免疫区内有多少千米? 导航页
导航页 核心重难探究 知识点二:垂径定理及其推论的应用 【例2】为防止禽流感蔓延,某地规定: 离疫点3千米范围内为捕杀区,所有禽类 全部捕杀;离疫点3至5千米范围内为免 疫区,所有禽类强制免疫;同时,对捕杀区和免疫区内的村庄、 道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病 区,如图,O为疫点,在捕杀区内的公路CD长为4千米,问这条公 路在该免疫区内有多少千米?

核心重难探究 思路点拨:过点O作OE⊥CD交CD于点E,连接OC,OA,在 Rt△OCE中求出 ,在Rt△OAE中求出 进而求出AC,求出答案 导航页
导航页 核心重难探究 思路点拨:过点O作OE⊥CD交CD于点E,连接OC,OA,在 Rt△OCE中求出 ,在Rt△OAE中求出 , 进而求出AC,求出答案

核心心重难探究 解:过点O作OE⊥CD于点E,连接OC,OA, .CD=4,.'.CE=2 免疫区 .0A=5,0C=3, 捕杀区 在Rt△0CE中,OE2=0C2-CE2=32-22=5. =上==0 在Rt△OAE中,AE=V0A2-0EZ=2√5. E D B .AC-AE-CE-2V5-2. .AC=BD,..AC+BD=4V5-4. '.这条公路在该免疫区内有(4V5-4)千米 导航页
导航页 核心重难探究 解:过点O作OE⊥CD于点E,连接OC,OA, ∵CD=4,∴CE=2. ∵OA=5,OC=3, 在Rt△OCE中,OE2=OC2 -CE2=3 2 -2 2=5. 在 Rt△OAE 中,AE= 𝑶𝑨𝟐-𝑶𝑬𝟐 =2 𝟓. ∴AC=AE-CE=2 𝟓-2. ∵AC=BD,∴AC+BD=4 𝟓-4. ∴这条公路在该免疫区内有(4 𝟓-4)千米