
家庭像四 4二次函数的应用 第1课时 利用二次函数求最大面积问题
4 二次函数的应用 第1课时 利用二次函数求最大面积问题

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.用二次函数求实际问题的最大面积问题,首先应当求出函 数表达式和自变量的取值范围,然后通过配方变形,或 利用顶点坐标公式求出它的最大值 导航页
导航页 基础自主梳理 1.用二次函数求实际问题的最大面积问题,首先应当求出函 数 和自变量的 ,然后通过配方变形,或 利用 公式求出它的最大值. 表达式 取值范围 顶点坐标

基础自主梳理 温馨提示 1.求得的最大值或最小值对应的自变量的取值必须在自变 量的取值范围内. 2.对于实际问题中的最大值,要注意有时并不是抛物线顶,点 的纵坐标原因是顶点的横坐标可能不在自变量的取值范围 之内,此时应根据二次函数的图象(抛物线的一段或一部分有 意义的点)进行解答 导航页
导航页 基础自主梳理 温馨提示 1.求得的最大值或最小值对应的自变量的取值必须在自变 量的取值范围内. 2.对于实际问题中的最大值,要注意有时并不是抛物线顶点 的纵坐标.原因是顶点的横坐标可能不在自变量的取值范围 之内,此时应根据二次函数的图象(抛物线的一段或一部分有 意义的点)进行解答
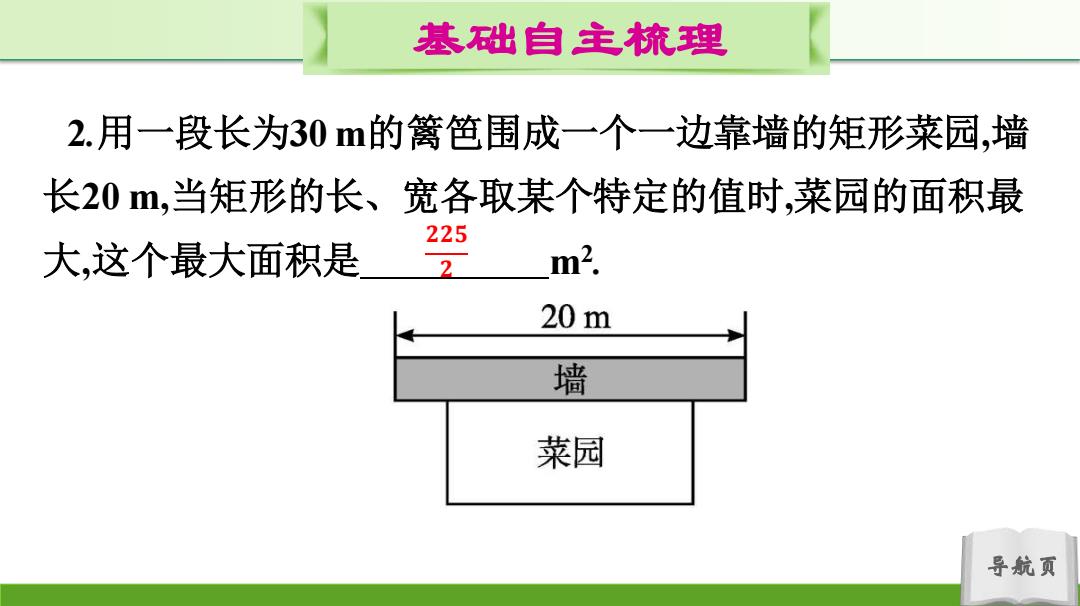
基础自主梳理 2.用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙 长20,当矩形的长、宽各取某个特定的值时,菜园的面积最 225 大,这个最大面积是 2 m2. 20m 墙 菜园 导航页
导航页 基础自主梳理 2.用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园,墙 长20 m,当矩形的长、宽各取某个特定的值时,菜园的面积最 大,这个最大面积是 m2 . 𝟐𝟐𝟓 𝟐

核心重难探究 知识点:最大面积问题 【例题】如图,为了节省材料,某水产养殖 区域① 户利用水库的岸堤(岸堤足够长)为一边,用 環 H G 区域③ 总长为80米的围网在水库中围成了①②③三 区域② 块矩形区域,而且这三块矩形区域的面积相等 E B 设BC的长度为x米,矩形区域ABCD的面积为y平方米 (1)求证:AE=2BE; (2)求y与x之间的函数关系式,并写出自变量x的取值范围; (3)x为何值时y有最大值?最大值是多少? 导航页
导航页 核心重难探究 知识点:最大面积问题 【例题】如图,为了节省材料,某水产养殖 户利用水库的岸堤(岸堤足够长)为一边,用 总长为80米的围网在水库中围成了①②③三 块矩形区域,而且这三块矩形区域的面积相等. 设BC的长度为x米,矩形区域ABCD的面积为y平方米. (1)求证:AE=2BE; (2)求y与x之间的函数关系式,并写出自变量x的取值范围; (3)x为何值时,y有最大值?最大值是多少?

核心重难探究 思路点拨:(1)根据三个矩形面积相等,得到矩形AEFD的面 积是矩形BCFE面积的 倍,可得出AE= BE;2) 设BE=M米,则有AE= a米,进而表示出y与x的关系 式,并求出x的取值范围即可3)利用二次函数的 。求 出y的最大值,以及此时x的值即可. 导航页
导航页 核心重难探究 思路点拨:(1)根据三个矩形面积相等,得到矩形AEFD的面 积是矩形BCFE面积的 倍,可得出AE= BE;(2) 设BE=a米,则有AE= a米,进而表示出y与x的关系 式,并求出x的取值范围即可;(3)利用二次函数的 求 出y的最大值,以及此时x的值即可

核心重难探究 ()证明:·三块矩形区域的面积相等, .'.矩形AEFD面积是矩形BCFE面积的2倍. 又EF是公共边,'AE=2BE (2)解:设BE=M米,则AE=2米.'AB=3a米 ∴.8a+2x=80,.a=8 0-2x 8 3a=302x子2+30c a80g20,40,.034 导航页
导航页 核心重难探究 (1)证明:∵三块矩形区域的面积相等, ∴矩形AEFD面积是矩形BCFE面积的2倍. 又EF是公共边,∴AE=2BE. (2)解:设BE=a米,则AE=2a米.∴AB=3a米. ∴8a+2x=80,∴a= 𝟖𝟎-𝟐𝒙 𝟖 . ∴y=3ax=3· 𝟖𝟎-𝟐𝒙 𝟖 ·x=- 𝟑 𝟒 x 2 +30x. ∵a= 𝟖𝟎-𝟐𝒙 𝟖 >0,∴x<40,∴0<x<40

核心重难探究 (3)解:y=2+30.=x-202+300(0<<40, 二次项系教为0, .函数图象开口向下, ∴.当x=20时y有最大值,最大值为300平方米. 导航页
导航页 核心重难探究 (3)解:∵y=- 𝟑 𝟒 x 2 +30x=- 𝟑 𝟒 (x-20)2 +300(0<x<40), 二次项系数为- 𝟑 𝟒 <0, ∴函数图象开口向下, ∴当x=20时,y有最大值,最大值为300平方米

核心重难探究 【方法归纳】 解决这类问题的关键是通过几何性质确定出二次函数的表 达式,然后确定其最大值,实际问题中自变量x的取值要使实际 问题有意义,因此在求二次函数的最值时,一定要注意自变量x 的取值范围. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题的关键是通过几何性质确定出二次函数的表 达式,然后确定其最大值,实际问题中自变量x的取值要使实际 问题有意义,因此在求二次函数的最值时,一定要注意自变量x 的取值范围