
家庭拿亚 第一章 直确三角形的边角关系 4解直角三角形
第一章 直角三角形的边角关系 4 解直角三角形

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.由直角三角形中已知 的元素,求出所有未知元 素的过程,叫做解直角三角形 2.在直角三角形的 6 个元素中,直角是已知元素,如 果再知道一条边 和第三个元素,那么这个三角形的 所有元素都可以确定下来 导航页
导航页 基础自主梳理 1.由直角三角形中 的元素,求出所有 元 素的过程,叫做解直角三角形. 2.在直角三角形的 个元素中,直角是已知元素,如 果再知道一条 和第三个元素,那么这个三角形的 所有元素都可以确定下来. 已知 未知 6 边
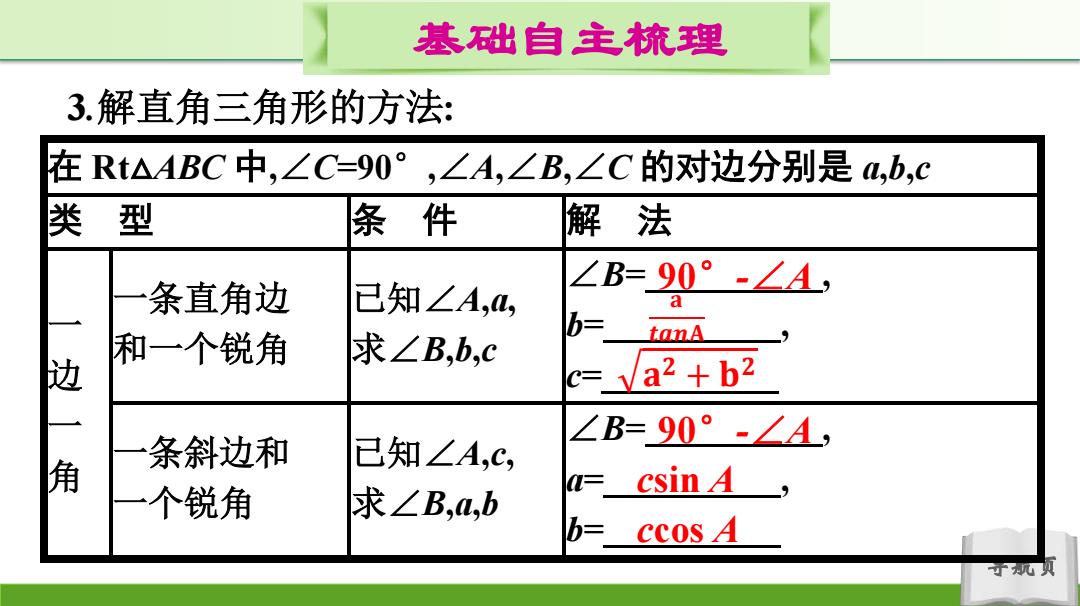
基础自主梳理 3.解直角三角形的方法: 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是4,b,c 类型 条件 解法 条直角边 已知∠A,, ∠B=90°-∠A, a b= 和一个锐角 求∠B,b,C tanA 边 c=va2 b2 条斜边和 ∠B=90°-∠A, 角 已知∠A,C, a=csin A 一个锐角 求∠B,a,b b= ccos 4 子玩项
导航页 基础自主梳理 3.解直角三角形的方法: 在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C 的对边分别是 a,b,c 类 型 条 件 解 法 一 边 一 角 一条直角边 和一个锐角 已知∠A,a, 求∠B,b,c ∠B= , b= , c= 一条斜边和 一个锐角 已知∠A,c, 求∠B,a,b ∠B= , a= , b= 90°-∠A 𝐚 𝒕𝒂𝒏𝐀 𝐚 𝟐 + 𝐛𝟐 90°-∠A csin A ccos A

基础自主梳理 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是,b,c 类型 条件 解法 已知a,b, =a2+b2 a 两条直角边 求C,∠A, tan A= b 两 ∠B tan B= (或∠B=90°-∠A) 边 已知4,C, b=vc2-a2 条斜边和 求b,∠A, sin A-c 条直角边 ∠B ∠B=90°-∠A 导航页
导航页 基础自主梳理 在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C 的对边分别是 a,b,c 类 型 条 件 解 法 两 边 两条直角边 已知 a,b, 求 c,∠A, ∠B c= , tan A= , tan B= (或∠B= ) 一条斜边和 一条直角边 已知 a,c, 求 b,∠A, ∠B b= , sin A= , ∠B= 𝐚 𝟐 + 𝐛𝟐 𝐚 𝐛 𝐛 𝐚 90°-∠A 𝐜 𝟐 -𝐚 𝟐 𝐚 𝐜 90°-∠A

核心重难探究 知识点一:解直角三角形 【例1】在Rt△ABC中,∠C=90°,已知BC=5V2,AC=5v6,解这 个直角三角形 思路点拨:(1)由BC与AC的值,利用哪个定理求出AB的值? (2)由BC与AC的值,怎么利用三角函数值求出∠A或∠B的值? 导航页
导航页 核心重难探究 知识点一:解直角三角形 【例 1】 在 Rt△ABC 中,∠C=90° ,已知 BC=5 𝟐,AC=5 𝟔,解这 个直角三角形. 思路点拨:(1)由BC与AC的值,利用哪个定理求出AB的值? (2)由BC与AC的值,怎么利用三角函数值求出∠A或∠B的值?

核心重难探究 解:如图所示, 在Rt△ABC中, .'∠C=90°,BC=5V2,AC=5V6, B '.AB=VAC2+BCZ=V√50+150=10V2. :anA= 5v2_3 AC =3) ∠A=30°, .∴∠B=90°-∠A=60°. 导航页
导航页 核心重难探究 解:如图所示, 在Rt△ABC中, ∵∠C=90°,BC=5 𝟐,AC=5 𝟔, ∴AB= 𝑨𝑪𝟐 + 𝑩𝑪𝟐 = 𝟓𝟎 + 𝟏𝟓𝟎=10 𝟐. ∵tan A=𝑩𝑪 𝑨𝑪 = 𝟓 𝟐 𝟓 𝟔 = 𝟑 𝟑 , ∴∠A=30° , ∴∠B=90°-∠A=60°

核心重难探究 【方法归纳】 1.解直角三角形就是求出所有的未知元素,不要误认为只求 锐角三角函数值 2.尽可能选包含所求元素与两个已知元素的关系式求解 3.在解答没有图形的问题时,通常是先根据题目要求正确地 画出图形,再数形结合求解 导航页
导航页 核心重难探究 【方法归纳】 1.解直角三角形就是求出所有的未知元素,不要误认为只求 锐角三角函数值. 2.尽可能选包含所求元素与两个已知元素的关系式求解. 3.在解答没有图形的问题时,通常是先根据题目要求正确地 画出图形,再数形结合求解

核心重难探究 知识点二:解直角三角形的应用 【例2】如图(1),窗框和窗扇用“滑块铰链”连接,图(3)是图(2) 中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂 DE安装在窗扇上,交点A处装有滑块,滑块可以左右滑动,支点 B,C,D始终在一条直线上,延长DE交MN于点FR已知 AC=DE=20 cm,AE=CD=10 cm,BD=40 cm. 导航页
导航页 核心重难探究 知识点二:解直角三角形的应用 【例2】 如图(1),窗框和窗扇用“滑块铰链”连接,图(3)是图(2) 中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂 DE安装在窗扇上,交点A处装有滑块,滑块可以左右滑动,支点 B,C,D始终在一条直线上,延长DE交MN于点F.已知 AC=DE=20 cm,AE=CD=10 cm,BD=40 cm

核心重难探究 窗扇 滑块 E E 窗框 铰链 M A BN M F A BN 图(1) 图(2) 图3) 导航页
导航页 核心重难探究 图(1) 图(2) 图(3)