
家庭值伞 *5 相以三确形判定定理的证明
*5 相似三角形判定定理的证明

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.相似三角形的判定定理 (1)两角分别 的两个三角形相似 (2)两边 且夹角 的两个三角形相似 (3)三边 的两个三角形相似 名师指导 相似三角形的三个判定定理的证明,思路相同,均是在较大 三角形上作一个与之相似又与较小三角形全等的三角形,使 定理获证,运用这些判定定理进行证明或计算时,应根据题设 条件灵活选用各种方法,使问题得以解决
基础自主梳理 1.相似三角形的判定定理 (1)两角分别相等 的两个三角形相似. (2)两边成比例 且夹角相等 的两个三角形相似. (3)三边成比例 的两个三角形相似. 名师指导 相似三角形的三个判定定理的证明,思路相同,均是在较大 三角形上作一个与之相似又与较小三角形全等的三角形,使 定理获证.运用这些判定定理进行证明或计算时,应根据题设 条件灵活选用各种方法,使问题得以解决

2.如图,在四边形ABCD中,ADIIBO,如果添加下列条件,那么 不能使得△ABC∽△DCA成立的是(D), A.∠BAC=∠ADC B.∠B=∠ACD C.AC2=AD·BC D DC AB B AC BC 合
2.如图,在四边形ABCD中,AD∥BC,如果添加下列条件,那么 不能使得△ABC∽△DCA成立的是( ). A.∠BAC=∠ADC B.∠B=∠ACD C.AC2=AD·BC D. 𝑫𝑪 𝑨𝑪 = 𝑨𝑩 𝑩𝑪 D

核心重难探究 知识点 相似三角形判定定理 【例题】如图,正方形ABCD的边长为2,AE=EB,MN=1,线段 MN的两端点在CB,CD上滑动,当CM为何值时,△AED与以点 M,N,C为顶点的三角形相似? E N M 思路点拨:由于未指明两三角形的对应关系,所以要分CM与 AE或AD分别是对应边两种情况进行求解
核心重难探究 知识点 相似三角形判定定理 【例题】如图,正方形ABCD的边长为2,AE=EB,MN=1,线段 MN的两端点在CB,CD上滑动,当CM为何值时,△AED与以点 M,N,C为顶点的三角形相似? 思路点拨:由于未指明两三角形的对应关系,所以要分CM与 AE或AD分别是对应边两种情况进行求解

解:DE=VAE2+ADz=V5. 当△AED∽△CMN时,AE:CM=DE:MN, 即1:CM=V5:1,酵得CM=5, 5 当△AED∽△CNM时,AD:CM=DE:MN, 即2:CM=V5:1,解得CM2 · 所以当CM=5或25时, 5 △AED与以M,N,C为项点的三角形相似. 合
解:DE= 𝐀𝐄 𝟐 + 𝐀𝐃𝟐 = 𝟓. 当△AED∽△CMN 时,AE∶CM=DE∶MN, 即 1∶CM= 𝟓∶1,解得 CM= 𝟓 𝟓 ; 当△AED∽△CNM 时,AD∶CM=DE∶MN, 即 2∶CM= 𝟓∶1,解得 CM=𝟐 𝟓 𝟓 . 所以当 CM= 𝟓 𝟓 或 𝟐 𝟓 𝟓 时, △AED 与以 M,N,C 为顶点的三角形相似
方法归纳】 三角形相似的判定 已知条件 需寻找的条件(或应用的方法) 平行线 两角对应相等 1.另一对角相等 一对角相等 2.夹等角的边成比例 两组对应边的比相等 1夹角相等 2.第三组边的比与之相等 直角三角形 1.一锐角相等 2.任意两组对应边成比例 1.顶角相等 等腰三角形 2.一组底角相等 3.底和腰的比相等
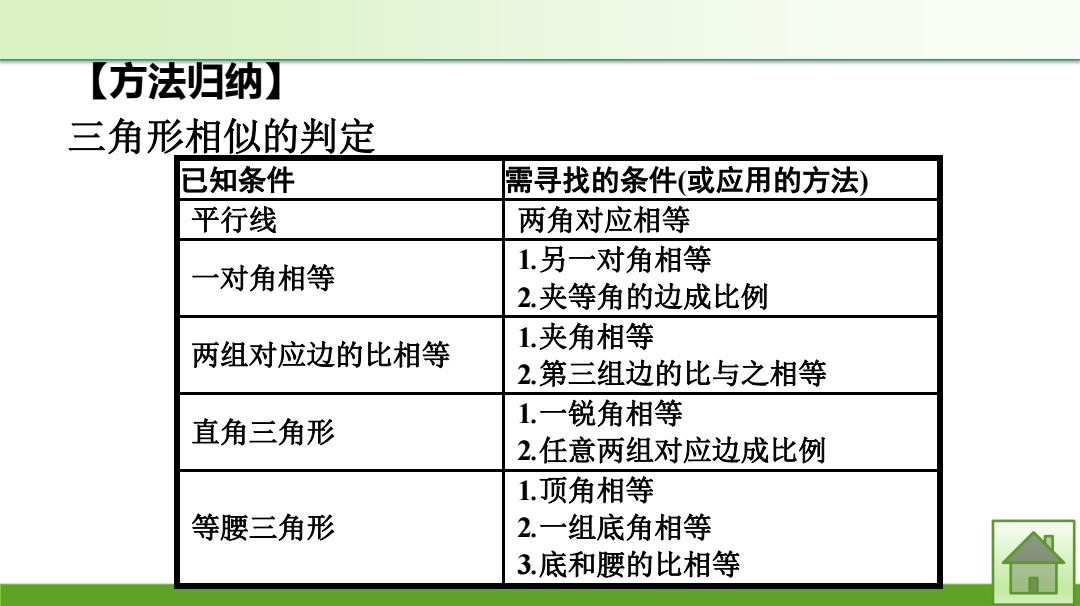
【方法归纳】 三角形相似的判定 已知条件 需寻找的条件(或应用的方法) 平行线 两角对应相等 一对角相等 1.另一对角相等 2.夹等角的边成比例 两组对应边的比相等 1.夹角相等 2.第三组边的比与之相等 直角三角形 1.一锐角相等 2.任意两组对应边成比例 等腰三角形 1.顶角相等 2.一组底角相等 3.底和腰的比相等

新知训川练巩固 1.已知下列说法:①不相似的三角形一定不全等;②不全等的 三角形一定不相似;③所有的钝角三角形都相似;④所有的等 腰三角形都相似其中正确的个数为(B), A.0 B.1 C.2 D.3 合
新知训练巩固 1.已知下列说法:①不相似的三角形一定不全等;②不全等的 三角形一定不相似;③所有的钝角三角形都相似;④所有的等 腰三角形都相似.其中正确的个数为( ). A.0 B.1 C.2 D.3 B

2.如图,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿选项图 示中的虚线剪开,剪下的阴影三角形与原来三角形不相似的 是(C), 00 789 A B C B C A B 78 B B D
2.如图,在△ABC中,∠A=78° ,AB=4,AC=6.将△ABC沿选项图 示中的虚线剪开,剪下的阴影三角形与原来三角形不相似的 是( C )

3.如图,E是口ABCD的边BA延长线上一点,连接EC,交AD于点F 求证:△EBC~△CDR E B 证明:.·四边形ABCD是平行四边形, .∠B=∠D,BE∥CD. '.∠E=∠DCF. '.△EBC∽△CDF. 合
3.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F. 求证:△EBC∽△CDF. 证明:∵四边形ABCD是平行四边形, ∴∠B=∠D,BE∥CD. ∴∠E=∠DCF. ∴△EBC∽△CDF