
家庭猴伞 第1课时 三角形相似的判定条件(1)
第1课时 三角形相似的判定条件(1)

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
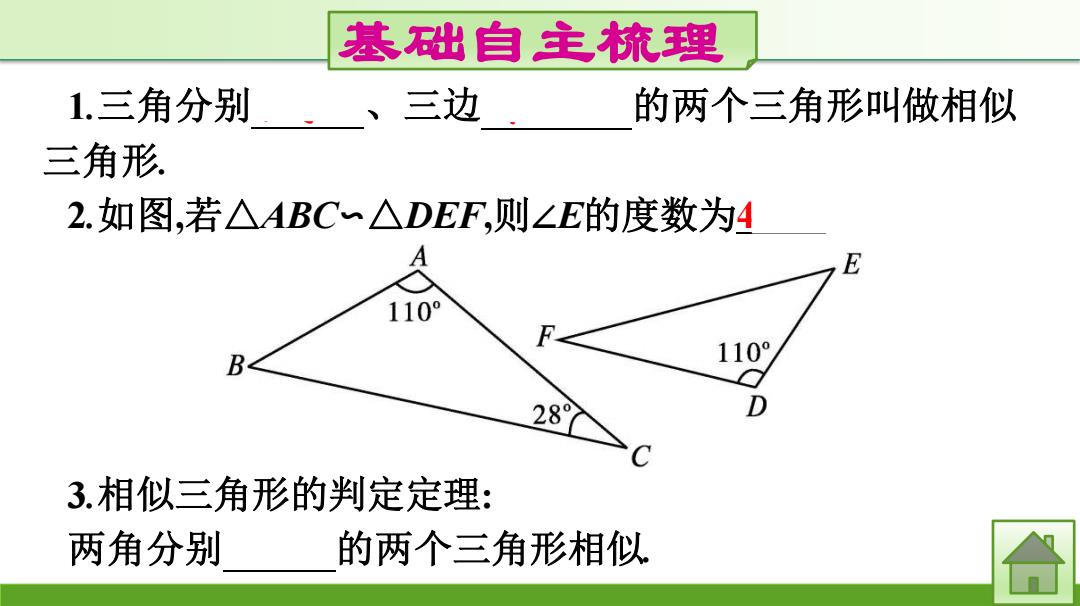
基础自主梳理 1.三角分别 、三边 的两个三角形叫做相似 三角形. 2.如图,若△ABC~△DEF,则∠E的度数为4 110° B 110° 28 D C 3.相似三角形的判定定理: 两角分别 的两个三角形相似
基础自主梳理 1.三角分别相等 、三边成比例 的两个三角形叫做相似 三角形. 2.如图,若△ABC∽△DEF,则∠E的度数为42° . 3.相似三角形的判定定理: 两角分别相等 的两个三角形相似

名师指导 由两组角对应相等判定三角形相似的方法是最常用的方法, 应用时关键是找准对应角.一般地,公共角、对顶角、直角、 同角(或等角)的余角(或补角)都是相等的角,应注意挖掘题中 隐含的条件
名师指导 由两组角对应相等判定三角形相似的方法是最常用的方法, 应用时关键是找准对应角.一般地,公共角、对顶角、直角、 同角(或等角)的余角(或补角)都是相等的角,应注意挖掘题中 隐含的条件
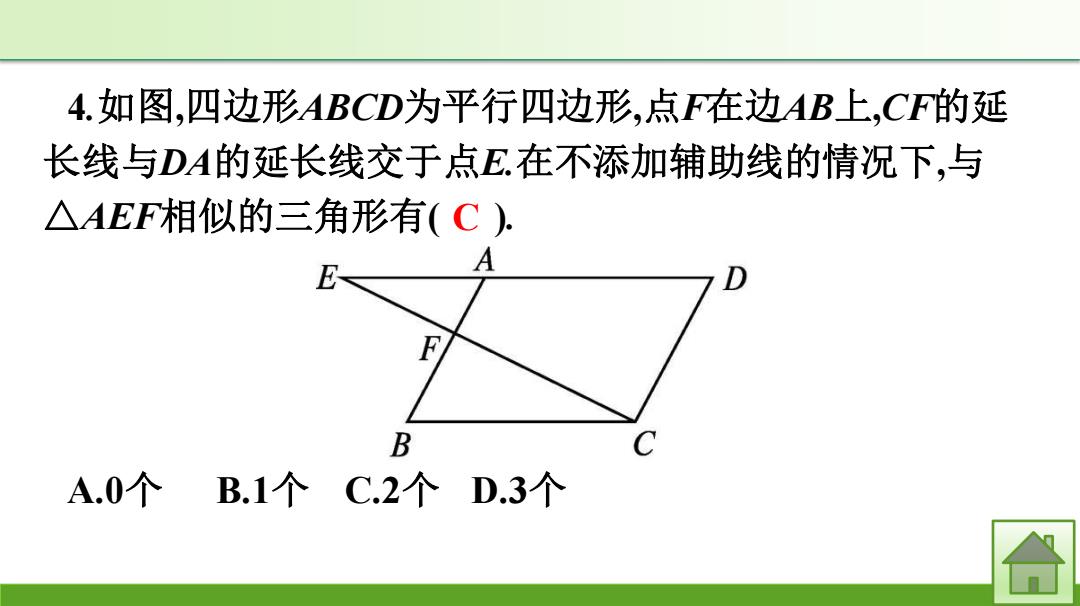
4.如图,四边形ABCD为平行四边形,点F在边AB上,CF的延 长线与DA的延长线交于点E在不添加辅助线的情况下,与 △AEF相似的三角形有(C). A F B A.0个 B.1个C.2个D.3个 合
4.如图,四边形ABCD为平行四边形,点F在边AB上,CF的延 长线与DA的延长线交于点E.在不添加辅助线的情况下,与 △AEF相似的三角形有( ). A.0个 B.1个 C.2个 D.3个 C
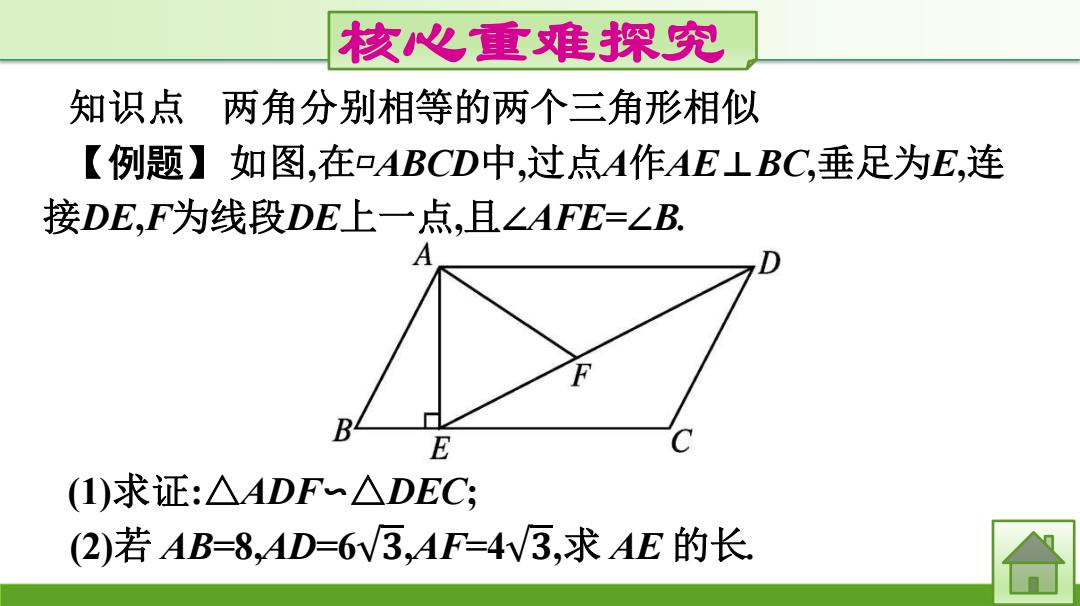
核心重难探究 知识点 两角分别相等的两个三角形相似 【例题】如图,在口ABCD中,过点A作AE⊥BC,垂足为E,连 接DE,F为线段DE上一点,且∠AFE=∠B. B E (I)求证:△ADF~△DEC; (2)若AB=8,AD=6V3,AF=4V3,求AE的长
核心重难探究 知识点 两角分别相等的两个三角形相似 【例题】如图,在▱ABCD中,过点A作AE⊥BC,垂足为E,连 接DE,F为线段DE上一点,且∠AFE=∠B. (1)求证:△ADF∽△DEC; (2)若 AB=8,AD=6 𝟑,AF=4 𝟑,求 AE 的长

思路点拨:(I)已知∠AFE=∠B,你能发现∠AFE与∠AFD,∠B 与∠C有什么关系吗? (2)由已知数据与(1)中的相似三角形,如何求AD的长?进而 如何再求AE的长? 合
思路点拨:(1)已知∠AFE=∠B,你能发现∠AFE与∠AFD, ∠B 与∠C有什么关系吗? (2)由已知数据与(1)中的相似三角形,如何求AD的长?进而 如何再求AE的长?

(1)证明:.四边形ABCD是平行四边形, '.AB∥CD,AD∥BC, '.∠C+∠B=180°,∠ADF=∠DEC. .∠AFD+∠AFE=180°,∠AFE=∠B, '.∠AFD=∠C. .△ADF∽△DEC. 合
(1)证明:∵四边形ABCD是平行四边形, ∴AB∥CD,AD∥BC, ∴∠C+∠B=180° ,∠ADF=∠DEC. ∵∠AFD+∠AFE=180° ,∠AFE=∠B, ∴∠AFD=∠C. ∴△ADF∽△DEC

(2)解:,四边形ABCD是平行四边形, ..CD=AB=8. 由(I为AADF∽aDEC是= AF CD' ..DE-AD-CD 6V3× 8-12. AF 4v 在Rt△ADE中, 由均联定理得AE=√DE2-AD2=√12-(6V32-6
(2)解:∵四边形ABCD是平行四边形, ∴CD=AB=8. 由(1)知△ADF∽△DEC,∴ 𝐀𝐃 𝐃𝐄 = 𝐀𝐅 𝐂𝐃 , ∴DE=𝐀𝐃·𝐂𝐃 𝐀𝐅 = 𝟔 𝟑×𝟖 𝟒 𝟑 =12. 在 Rt△ADE 中, 由勾股定理得 AE= 𝐃𝐄𝟐-𝐀𝐃𝟐 = 𝟏𝟐𝟐-(𝟔 𝟑) 𝟐 =6
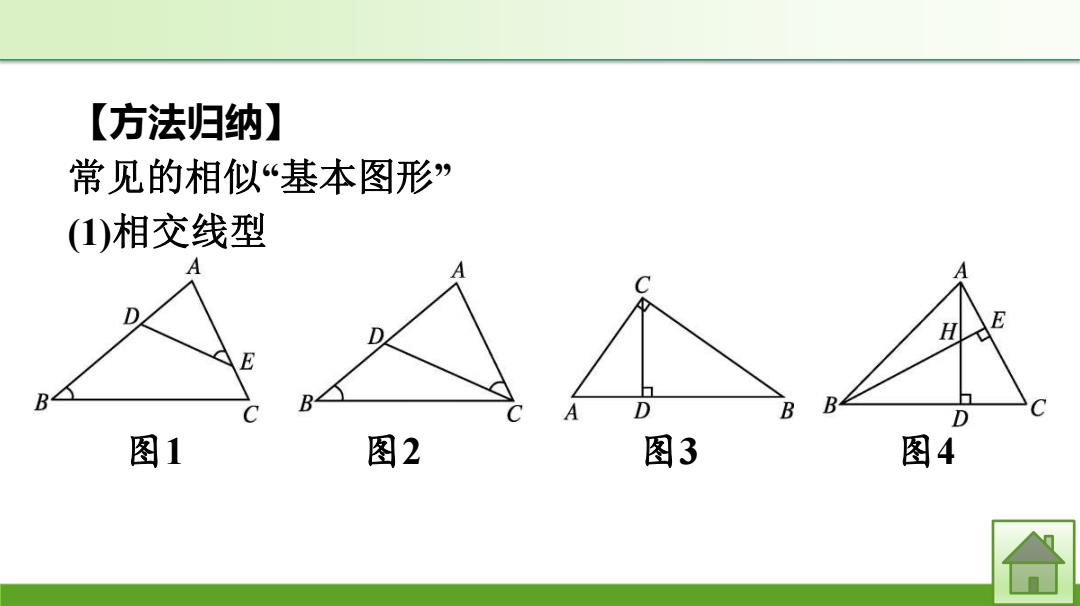
【方法归纳】 常见的相似“基本图形” (1)相交线型 A C D H E D E B< B D B B D C 图1 图2 图3 图4
【方法归纳】 常见的相似“基本图形” (1)相交线型 图1 图2 图3 图4