
家庭值四 第4课时 黄金分割
第4课时 黄金分割

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 AC BC 1.一般地,点C把线段AB分成两条线段AC和BC,如果AB=AC 那么称线段AB被点C黄金分割,点C叫做线段AB的 AC与AB的比叫做黄金比. 合
基础自主梳理 1.一般地,点C把线段AB分成两条线段AC和BC,如果________, 那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点 , AC与AB的比叫做黄金比. 𝐀𝐂 𝐀𝐁 = 𝐁𝐂 𝐀𝐂

温馨提示 黄金分割是指将整体一分为二,较大部分与整体部分的比值 等于较小部分与较大部分的比值,其比值约为0.618.这个比例 被公认为是最能引起美感的比例,因此被称为黄金分割.一条 线段的黄金分割点有两个.黄金三角形是一个等腰三角形,其 底与腰的长度比为黄金比值将一个正五边形的所有对角线 连接起来组成五角星,在五角星中可以找到的所有线段之间 的长度关系都符合黄金分割比
温馨提示 黄金分割是指将整体一分为二,较大部分与整体部分的比值 等于较小部分与较大部分的比值,其比值约为0.618.这个比例 被公认为是最能引起美感的比例,因此被称为黄金分割.一条 线段的黄金分割点有两个.黄金三角形是一个等腰三角形,其 底与腰的长度比为黄金比值.将一个正五边形的所有对角线 连接起来组成五角星,在五角星中可以找到的所有线段之间 的长度关系都符合黄金分割比

2.若点M将线段AB黄金分割(AM>BM0,则下列各式不正确 的是(C) A.AM BM-AB AM B.4M=5 AB 2 C.EM-E-AB D.AM≈0.618AB 2 合
2.若点M将线段AB黄金分割(AM>BM),则下列各式不正确 的是( ). A.AM∶BM=AB∶AM B.AM= 𝟓-𝟏 𝟐 AB C.BM= 𝟓-𝟏 𝟐 AB D.AM≈0.618AB C
核心重难探究 知识点 黄金分割 【例题】定义:如图1,点C在线段AB上,若满足AC2=BCAB, 则称点C为线段AB的一个黄金分割点.如图2,在△ABC中, AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D D A C B B 图1 图2 合
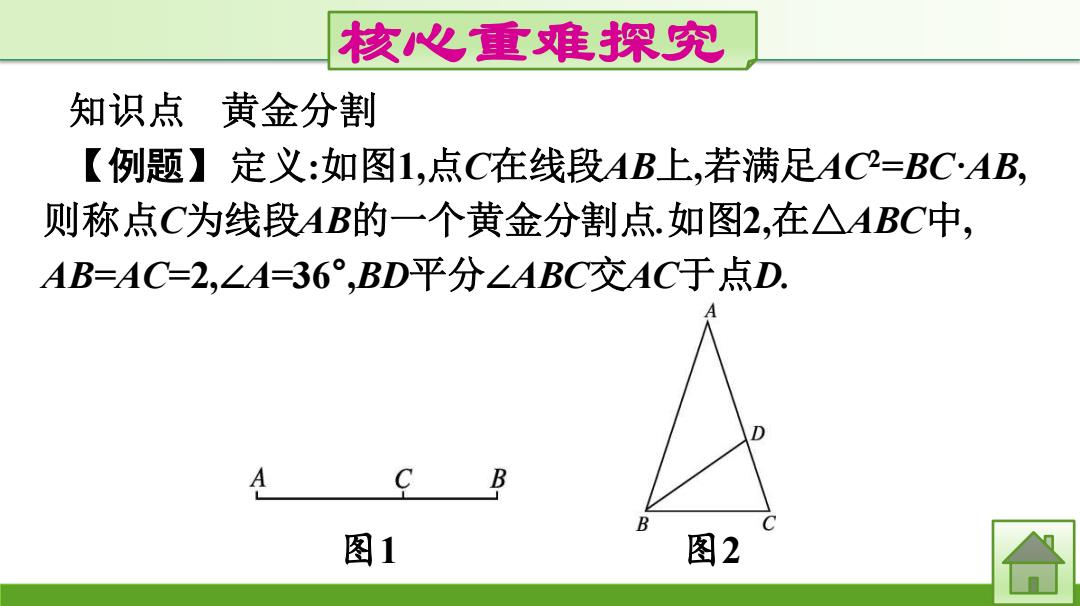
核心重难探究 知识点 黄金分割 【例题】定义:如图1,点C在线段AB上,若满足AC2=BC·AB, 则称点C为线段AB的一个黄金分割点.如图2,在△ABC中, AB=AC=2,∠A=36° ,BD平分∠ABC交AC于点D. 图1 图2

(1)求证:点D是线段AC的黄金分割点; (2)求线段BC的长 思路点拨:1)利用已知条件,求解线段AD,DC,AC之间的数量 关系,进而求证;(2)利用(1)中结论构建方程可求得AD的值,即 得线段BC的长」
(1)求证:点D是线段AC的黄金分割点; (2)求线段BC的长. 思路点拨:(1)利用已知条件,求解线段AD,DC,AC之间的数量 关系,进而求证;(2)利用(1)中结论构建方程可求得AD的值,即 得线段BC的长

(1)证明:.∠A=36°,AB=AC, .∴.∠ABC=∠C=72°. 又BD平分∠ABC,∴.∠DBC=∠ABD=36°. 在△ABC与△BDC中,∠A=∠DBC,∠C=∠C, '.△ABC△BDC, E=即B(2-CaC .‘∠A=36°,∠ABD=36°,.BD=AD, 同理BD=BC.∴,AD=BC,∴AD2=DC·AC. .点D是线段AC的黄金分割制点. 合
(1)证明:∵∠A=36°,AB=AC, ∴∠ABC=∠C=72° . 又BD平分∠ABC,∴∠DBC=∠ABD=36° . 在△ABC与△BDC中,∠A=∠DBC,∠C=∠C, ∴△ABC∽△BDC, ∴ 𝐁𝐂 𝐀𝐂 = 𝐃𝐂 𝐁𝐂 ,即 BC2 =DC·AC. ∵∠A=36° ,∠ABD=36° ,∴BD=AD. 同理BD=BC.∴AD=BC,∴AD2=DC·AC. ∴点D是线段AC的黄金分割点

(2)解:设AD=x,由(1)中的结论, 得x2=2(2-x),即x2+2x-4=0, 解得x1=V5-1,x2=-V5-1(舍去). ∴.AD=V5-1. 又AD=BC,'.BC=V5-1. 合
(2)解:设 AD=x,由(1)中的结论, 得 x 2 =2(2-x),即 x 2 +2x-4=0, 解得 x1= 𝟓-1,x2=- 𝟓-1(舍去). ∴AD= 𝟓-1. 又 AD=BC,∴BC= 𝟓-1

【方法归纳】 黄金分割的应用与证明: (1)已知一点为线段的一个黄金分割点,首先应明确它分线 段所得到的较长线段,然后应用黄金比解决问题, (2)要证明一个点为线段的一个黄金分割点,可以通过计算 来证明,即证明较长线段的平方等于较短线段与原线段长之 积
【方法归纳】 黄金分割的应用与证明: (1)已知一点为线段的一个黄金分割点,首先应明确它分线 段所得到的较长线段,然后应用黄金比解决问题. (2)要证明一个点为线段的一个黄金分割点,可以通过计算 来证明,即证明较长线段的平方等于较短线段与原线段长之 积