
家庭值少 2 平行线分线段成比例
2 平行线分线段成比例

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.平行线分线段成比例 (1)基本事实:两条直线被一组平行线所截,所得的对应线段 (2)推论:平行于三角形一边的直线与其他两边相交,截得的 对应线段
基础自主梳理 1.平行线分线段成比例 (1)基本事实:两条直线被一组平行线所截,所得的对应线段 成比例 . (2)推论:平行于三角形一边的直线与其他两边相交,截得的 对应线段成比例

名师指导 平行线分线段成比例定理的形象记忆 如图AB∥CD∥EF,则AC=BD, CE DF AC BD CE DF DF'AC BD'AE BF'AE BE 若将线段AC,BD称为上,线段CE,DF称 A 为下,线段AE,BF称为全,上述比例式,用 形象的语言可简述为: 卡=卡= E= 下 =下 下’上一上’全一 全’
名师指导 平行线分线段成比例定理的形象记忆 如图,AB∥CD∥EF,则 𝑨𝑪 𝑪𝑬 = 𝑩𝑫 𝑫𝑭 , 𝑪𝑬 𝑨𝑪 = 𝑫𝑭 𝑩𝑫 , 𝑨𝑪 𝑨𝑬 = 𝑩𝑫 𝑩𝑭 , 𝑪𝑬 𝑨𝑬 = 𝑫𝑭 𝑩𝑭 , … 若将线段AC,BD称为上,线段CE,DF称 为下,线段AE,BF称为全,上述比例式,用 形象的语言可简述为: 上 下 = 上 下 , 下 上 = 下 上 , 上 全 = 上 全 , 下 全 = 下 全 , …
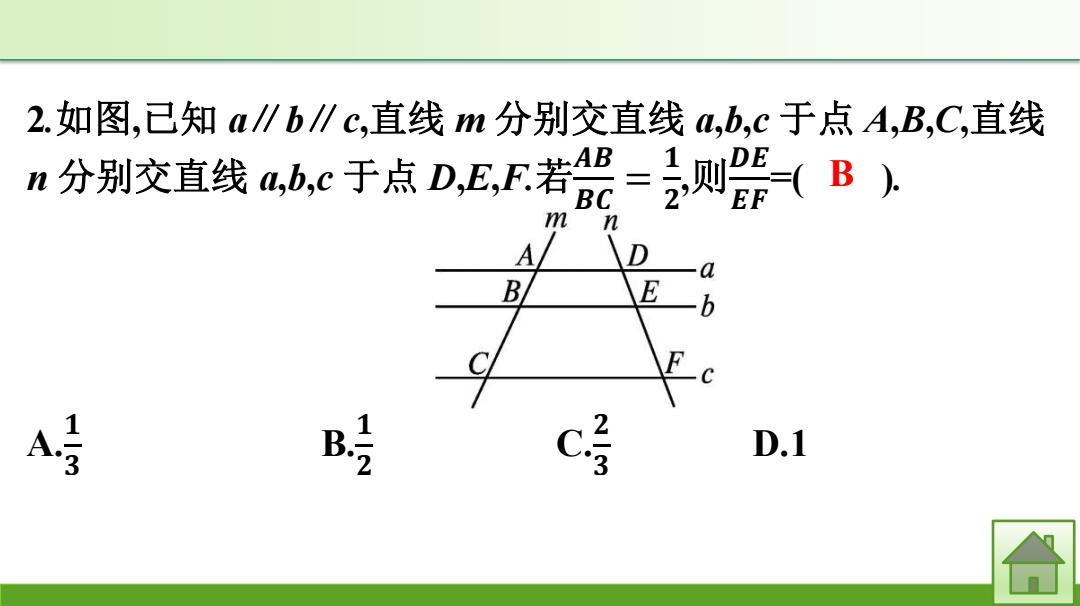
2.如图,已知a∥b∥c,直线m分别交直线,b,c于点A,B,C,直线 n分别交直线abc于点D,ER若=则2器B m n A D a B E b F A号 c D.1 合
2.如图,已知 a∥b∥c,直线 m 分别交直线 a,b,c 于点 A,B,C,直线 n 分别交直线 a,b,c 于点 D,E,F.若 𝑨𝑩 𝑩𝑪 = 𝟏 𝟐 ,则 𝑫𝑬 𝑬𝑭 =( ). A. 𝟏 𝟑 B. 𝟏 𝟐 C. 𝟐 𝟑 D.1 B
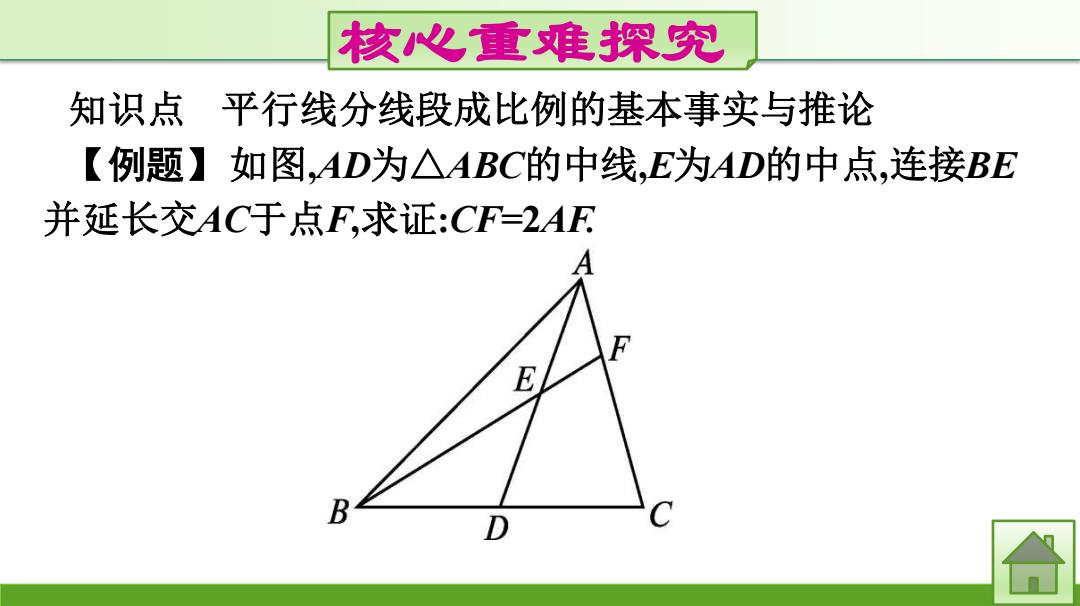
核心重难探究 知识点 平行线分线段成比例的基本事实与推论 【例题】如图,AD为△ABC的中线,E为AD的中点,连接BE 并延长交AC于点F,求证:CF=2AF E B D C 合
核心重难探究 知识点 平行线分线段成比例的基本事实与推论 【例题】如图,AD为△ABC的中线,E为AD的中点,连接BE 并延长交AC于点F,求证:CF=2AF

思路点拨:)如何作平行线构造出平行线分线段成比例的 基本图形? (2)若作DHII BF交AC于点H,你能发现几个基本图形? 3)若作DMILAC交BF于点M,能否证明CF=2AF? 证明:过点D作DHI BF交AC于点H, FH AE = AF HC'ED FH .'BD=CD,AE=DE, .'.FH=HC=AF, CF=2FH=2AF
思路点拨:(1)如何作平行线构造出平行线分线段成比例的 基本图形? (2)若作DH∥BF交AC于点H,你能发现几个基本图形? (3)若作DM∥AC交BF于点M,能否证明CF=2AF? 证明:过点D作DH∥BF交AC于点H, 则 𝐁𝐃 𝐂𝐃 = 𝐅𝐇 𝐇𝐂 , 𝐀𝐄 𝐄𝐃 = 𝐀𝐅 𝐅𝐇 . ∵BD=CD,AE=DE, ∴FH=HC=AF, ∴CF=2FH=2AF

【方法归纳】 1.平行线分线段成比例辅助线作法“三原则:(1)构造“A型” 图形;2)构造X型”图形;3)过交点或分点作辅助线. 2.运用平行线分线段的基本事实与推论时,一要看清平行线 组;二要找准平行线组截得的对应线段,否则就会产生错误
【方法归纳】 1.平行线分线段成比例辅助线作法“三原则”:(1)构造“A型” 图形;(2)构造“X型”图形;(3)过交点或分点作辅助线. 2.运用平行线分线段的基本事实与推论时,一要看清平行线 组;二要找准平行线组截得的对应线段,否则就会产生错误

新知训川练织固 1.如图,已知一组平行线allbllc,.被直线m,n所截,交点分别为 A,B,C和D,E,F,且AB=3,BC=4,EF=4.8,则DE=(C), D B A.7.2 B.6.4 C.3.6 D.2.4 m 合
新知训练巩固 1.如图,已知一组平行线a∥b∥c,被直线m,n所截,交点分别为 A,B,C和D,E,F,且AB=3,BC=4,EF=4.8,则DE=( ). A.7.2 B.6.4 C.3.6 D.2.4 C
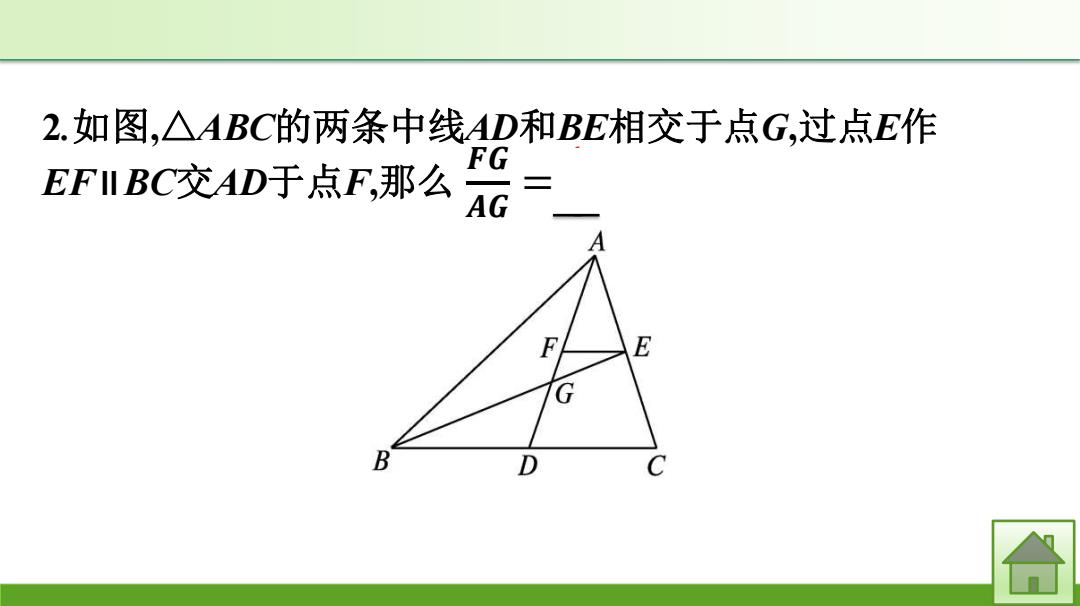
2.如图,△ABC的两条中线AD和BE相交于点G,过点E作 EFI BC交AD于点F,那么 A ② E G B D C
2.如图,△ABC的两条中线AD和BE相交于点G,过点E作 EF∥BC交AD于点F,那么 . 𝑭𝑮 𝑨𝑮 = 𝟏 𝟒