
家庭猴伞 第3课时 矩形的性质与判定的综合应用
第3课时 矩形的性质与判定的综合应用

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
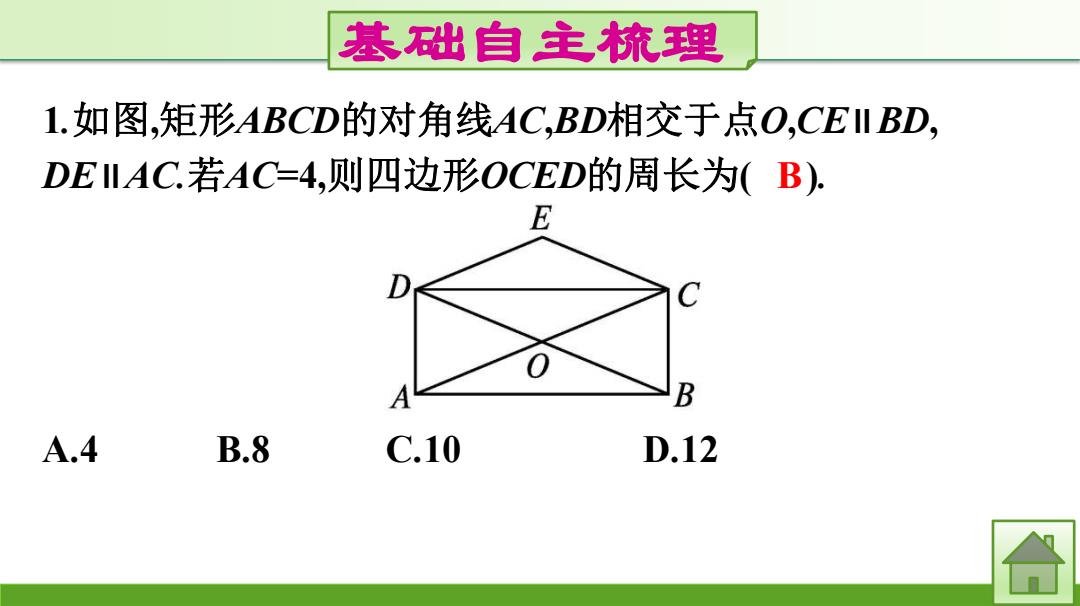
基础自主梳理 1.如图,矩形ABCD的对角线AC,BD相交于点O,CEI BD, DEILAC.若AC=4,则四边形OCED的周长为(B). E B A.4 B.8 C.10 D.12 合
基础自主梳理 1.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD, DE∥AC.若AC=4,则四边形OCED的周长为( ). A.4 B.8 C.10 D.12 B
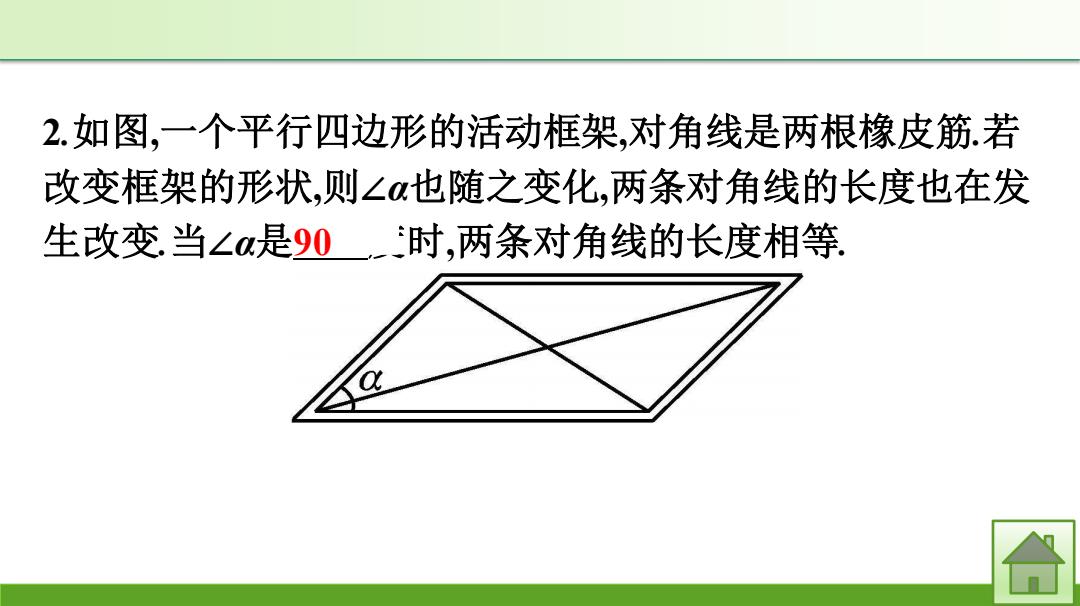
2.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若 改变框架的形状,则∠α也随之变化,两条对角线的长度也在发 生改变当∠a是90-时,两条对角线的长度相等
2.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若 改变框架的形状,则∠α也随之变化,两条对角线的长度也在发 生改变.当∠α是90 度时,两条对角线的长度相等
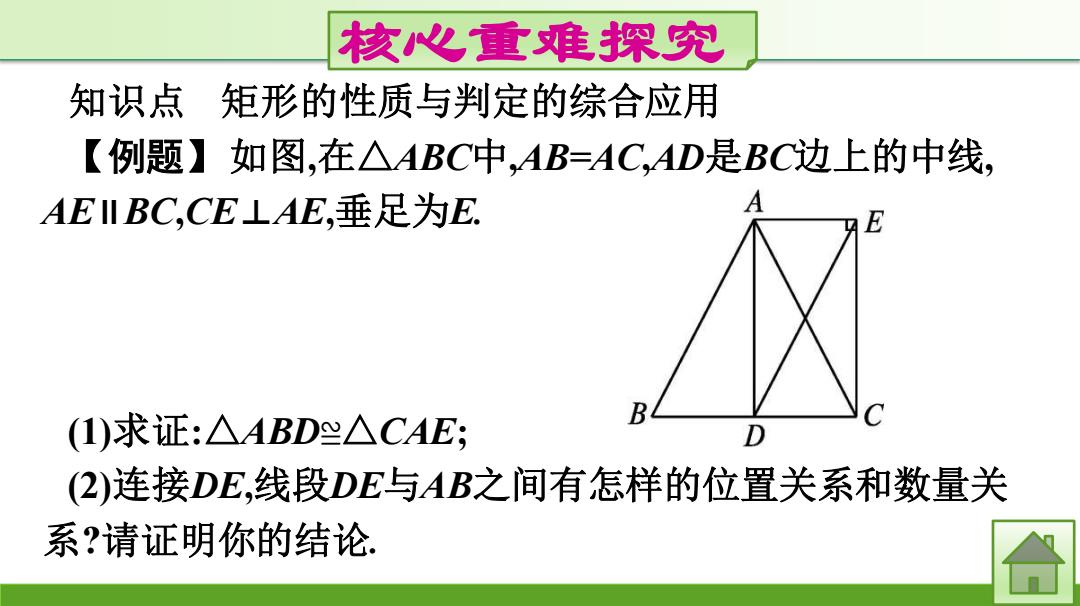
核心重难探究 知识点 矩形的性质与判定的综合应用 【例题】如图,在△ABC中,AB=AC,AD是BC边上的中线, AE I BC,CE⊥AE,垂足为E. (1)求证:△ABD≌△CAE; B D (2)连接DE,线段DE与AB之间有怎样的位置关系和数量关 系?请证明你的结论
核心重难探究 知识点 矩形的性质与判定的综合应用 【例题】如图,在△ABC中,AB=AC,AD是BC边上的中线, AE∥BC,CE⊥AE,垂足为E. (1)求证:△ABD≌△CAE; (2)连接DE,线段DE与AB之间有怎样的位置关系和数量关 系?请证明你的结论

思路点拨:1)△ABD是什么特殊的三角形?四边形ADCE是 什么特殊的四边形? (2)四边形ABDE是什么特殊的四边形?
思路点拨:(1)△ABD是什么特殊的三角形?四边形ADCE是 什么特殊的四边形? (2)四边形ABDE是什么特殊的四边形?

(1)证明:.AB=AC,AD是BC边上的中线, .∴.AD⊥BC,BD=CD,∠ADC=90°. .AEII BC,‘.∠EAD=180°-∠ADC=90°. CE⊥AE,∴.∠AEC=∠EAD=∠ADC=90°, .四边形ADCE是矩形,∴AD=CE. 又AB=AC,'Rt△ABD Rt△CAE
(1)证明:∵AB=AC,AD是BC边上的中线, ∴AD⊥BC,BD=CD,∠ADC=90° . ∵AE∥BC,∴∠EAD=180°-∠ADC=90° . ∵CE⊥AE,∴∠AEC=∠EAD=∠ADC=90° , ∴四边形ADCE是矩形,∴AD=CE. 又AB=AC,∴Rt△ABD≌Rt△CAE

(2)解:DEIAB,DE=AB.证明如下: 四边形ADCE是矩形, ∴.AE=CD=BD,AE II BD, .四边形ABDE是平行四边形, .∴.DEIAB,DE=AB
(2)解:DE∥AB,DE=AB.证明如下: ∵四边形ADCE是矩形, ∴AE=CD=BD,AE∥BD, ∴四边形ABDE是平行四边形, ∴DE∥AB,DE=AB

【名师点津】 证明两条线段相等,除了运用全等三角形、等腰三角形的知 识外,还可运用平行四边形的对边相等、对角线互相平分、 矩形的对角线相等来证明. 合
【名师点津】 证明两条线段相等,除了运用全等三角形、等腰三角形的知 识外,还可运用平行四边形的对边相等、对角线互相平分、 矩形的对角线相等来证明
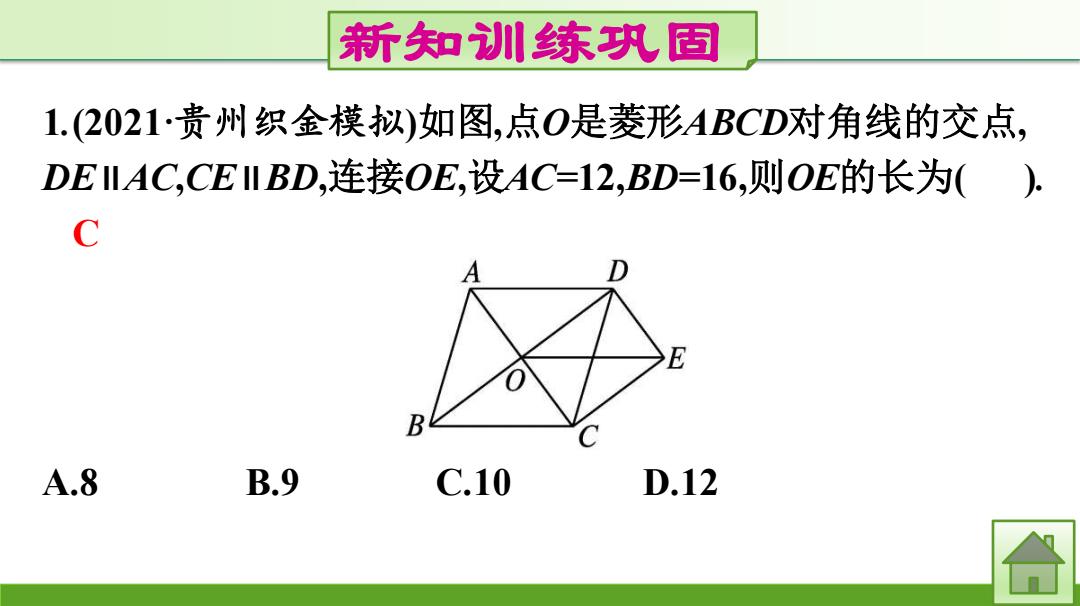
新知训川练织固 1.(2021·贵州织金模拟)如图,点O是菱形ABCD对角线的交点, DEIAC,CE IIBD,连接OE,设AC=12,BD=16,则OE的长为(), C E B A.8 B.9 C.10 D.12 合
新知训练巩固 1.(2021·贵州织金模拟)如图,点O是菱形ABCD对角线的交点, DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( ). C A.8 B.9 C.10 D.12