
家庭值亚 第l课时 菱形的性质
第1课时 菱形的性质

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基出自主梳理 1.菱形的定义 有一组邻边相等的 叫做菱形. 温馨提示 1菱形的定义包含两层含义:一是平行四边形,二是有一组邻 边相等,二者缺一不可 2.菱形是特殊的平行四边形,它具有平行四边形的所有性质, 又有它特有的性质菱形既是轴对称图形,又是中心对称图形, 这为解决图形的旋转和对称提供了重要依据
基础自主梳理 1.菱形的定义 有一组邻边相等的平行四边形 叫做菱形. 温馨提示 1.菱形的定义包含两层含义:一是平行四边形,二是有一组邻 边相等,二者缺一不可. 2.菱形是特殊的平行四边形,它具有平行四边形的所有性质, 又有它特有的性质.菱形既是轴对称图形,又是中心对称图形, 这为解决图形的旋转和对称提供了重要依据

2.菱形的性质定理 (1)菱形的四条边 (2)菱形的对角线 合
2.菱形的性质定理 (1)菱形的四条边相等 . (2)菱形的对角线互相垂直
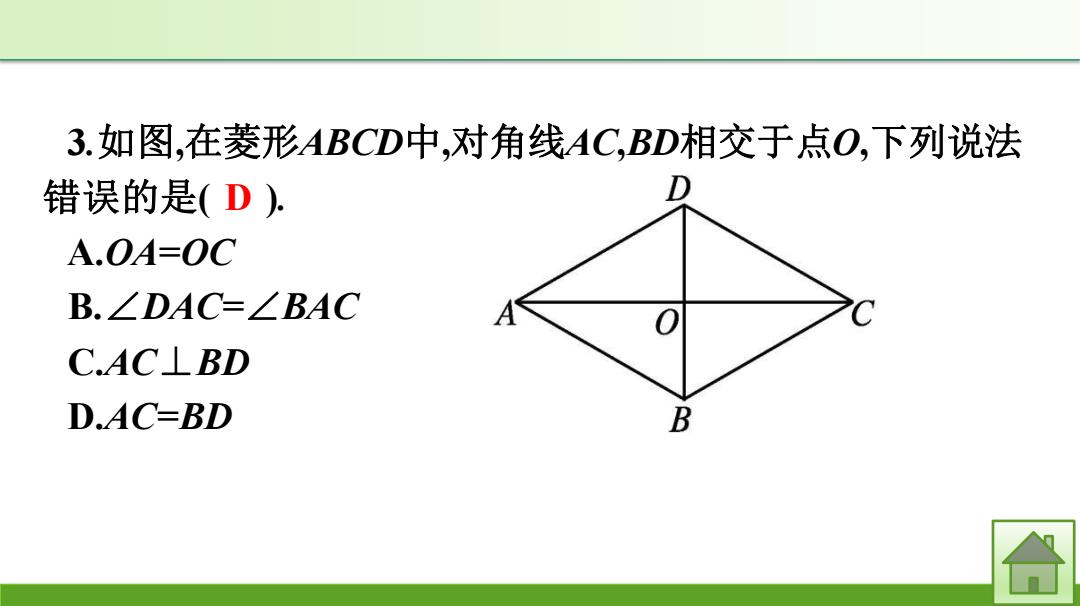
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列说法 错误的是(D) A.OA-OC B.∠DAC=∠BAC C.AC⊥BD D.AC-BD B
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列说法 错误的是( ). A.OA=OC B.∠DAC=∠BAC C.AC⊥BD D.AC=BD D
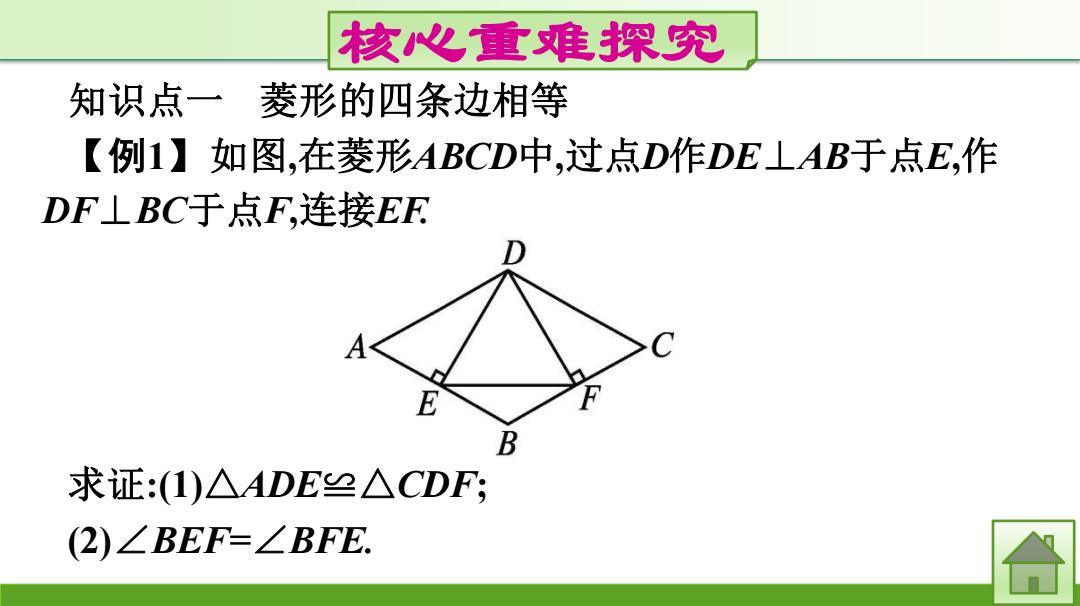
核心重难探究 知识点一菱形的四条边相等 【例1】如图,在菱形ABCD中,过点D作DE⊥AB于点E,作 DF⊥BC于点F,连接EF E B 求证:(1)△ADE≌△CDF; 2)∠BEF=∠BFE. 合
核心重难探究 知识点一 菱形的四条边相等 【例1】如图,在菱形ABCD中,过点D作DE⊥AB于点E,作 DF⊥BC于点F,连接EF. 求证:(1)△ADE≌△CDF; (2)∠BEF=∠BFE

思路点拨:(1)△ADE与△CDF中有哪些线段相等?有哪些角 相等?为什么? (2)在△BEF中,BE与BF是否相等?
思路点拨:(1)△ADE与△CDF中有哪些线段相等?有哪些角 相等?为什么? (2)在△BEF中,BE与BF是否相等?

证明:1).四边形ABCD是菱形, '.AD=CD,∠A=∠C(菱形的四条边相等,对角相等). .DE⊥AB,DF⊥BC,'.∠AED=∠CFD=90°. (LA=∠C, 在△ADE与△CDF中, ∠AED=∠CFD, (AD CD, '.△ADE≌△CDF(AAS). (2).四边形ABCD是菱形,∴.AB=BC(菱形的四条边相等) 由(1)得△ADE≌△CDF,∴.AE=CF .AB-AE=BC-CF,∴.BE=BF,'.∠BEF=∠BFE
证明:(1)∵四边形ABCD是菱形, ∴AD=CD,∠A=∠C(菱形的四条边相等,对角相等). ∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90° . 在△ADE 与△CDF 中,∵ ∠𝐀 = ∠𝐂, ∠𝐀𝐄𝐃 = ∠𝐂𝐅𝐃, 𝐀𝐃 = 𝐂𝐃, ∴△ADE≌△CDF(AAS). (2)∵四边形ABCD是菱形,∴AB=BC(菱形的四条边相等). 由(1)得△ADE≌△CDF,∴AE=CF. ∴AB-AE=BC-CF,∴BE=BF,∴∠BEF=∠BFE

【方法归纳】 菱形的四条边相等,依据菱形的性质,可为证明三角形全等 创造条件 合
【方法归纳】 菱形的四条边相等,依据菱形的性质,可为证明三角形全等 创造条件
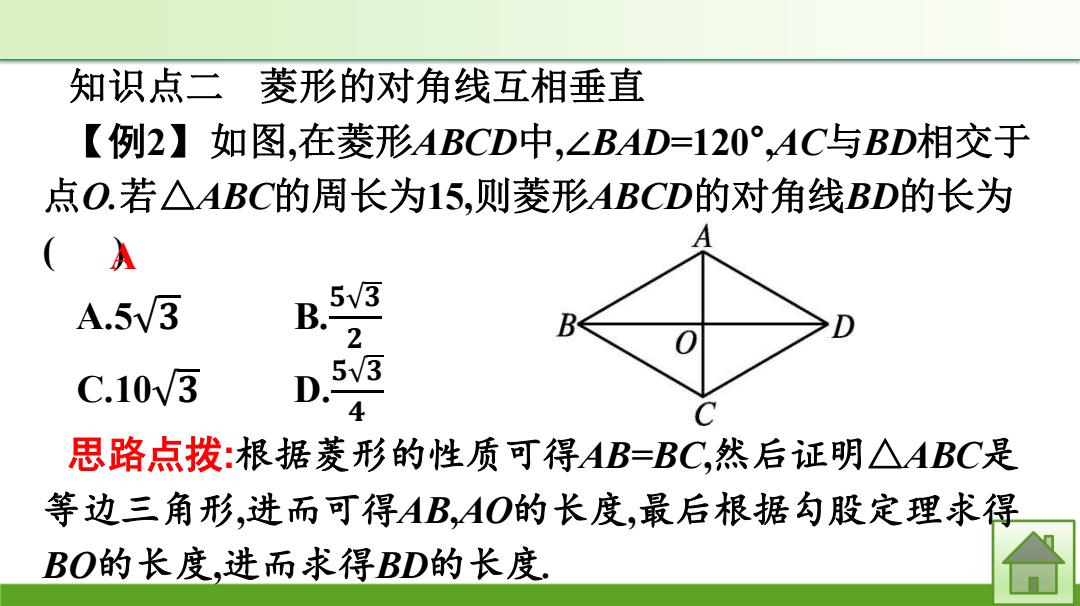
知识点二菱形的对角线互相垂直 【例2】如图,在菱形ABCD中,∠BAD=120°,AC与BD相交于 点O.若△ABC的周长为15,则菱形ABCD的对角线BD的长为 (A A.5v3 B. V3 2 C.103 D 5v3 4 思路点拨:根据菱形的性质可得AB=BC,然后证明△ABC是 等边三角形,进而可得AB,AO的长度,最后根据勾股定理求得 BO的长度,进而求得BD的长度
知识点二 菱形的对角线互相垂直 【例2】如图,在菱形ABCD中,∠BAD=120° ,AC与BD相交于 点O.若△ABC的周长为15,则菱形ABCD的对角线BD的长为 ( ). A.5 𝟑 B. 𝟓 𝟑 𝟐 C.10 𝟑 D. 𝟓 𝟑 𝟒 思路点拨:根据菱形的性质可得AB=BC,然后证明△ABC是 等边三角形,进而可得AB,AO的长度,最后根据勾股定理求得 BO的长度,进而求得BD的长度. A