
家庭值亚 第2课时 菱形的判定
第2课时 菱形的判定

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自住梳理 1.菱形的判定定理 (1)对角线 的平行四边形是菱形 (2)四边 的四边形是菱形
基础自主梳理 1.菱形的判定定理 (1)对角线互相垂直 的平行四边形是菱形. (2)四边相等 的四边形是菱形

名师指导 菱形与平行四边形相比,它的边比较特殊,同时,它的对角线 也与平行四边形有所不同,所以菱形的判定从边(一组邻边相 等的平行四边形和对角线(对角线互相垂直的平行四边形是 菱形)两方面进行.又因为菱形的边的特殊性,所 以在四边形的基础上添加“四条边都相等”这一条件,也可以 得到菱形
名师指导 菱形与平行四边形相比,它的边比较特殊,同时,它的对角线 也与平行四边形有所不同,所以菱形的判定从边(一组邻边相 等的平行四边形)和对角线(对角线互相垂直的平行四边形是 菱形)两方面进行.又因为菱形的边的特殊性,所 以在四边形的基础上添加“四条边都相等”这一条件,也可以 得到菱形
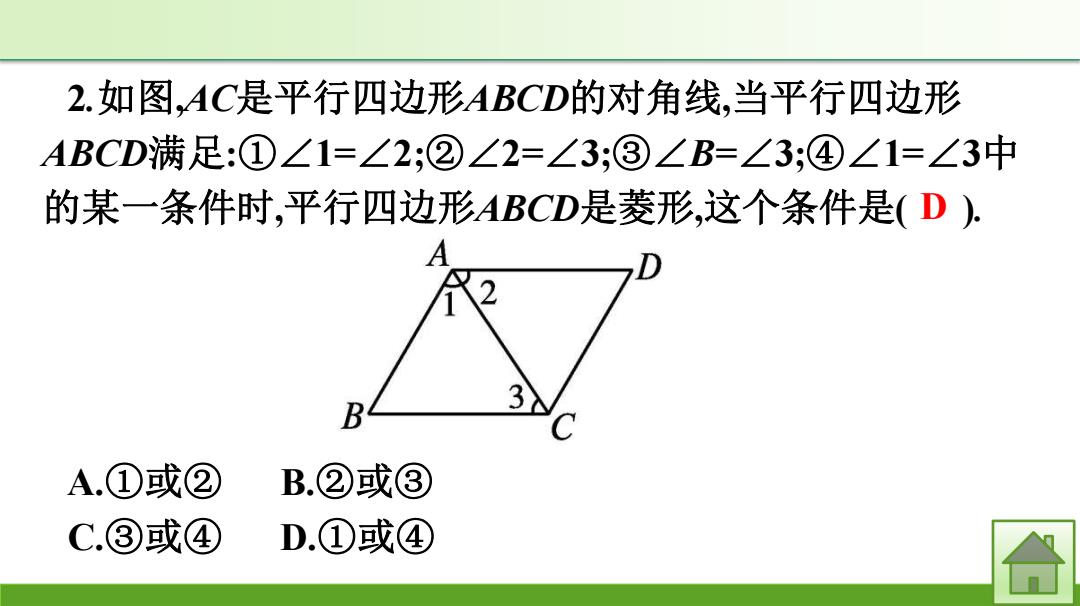
2.如图,AC是平行四边形ABCD的对角线,当平行四边形 ABCD满足:①∠1=∠2;②∠2=∠3;③∠B=∠3;④∠1=∠3中 的某一条件时,平行四边形ABCD是菱形,这个条件是(D), B A.①或② B.②或③ C.③或④ D.①或④ 合
2.如图,AC是平行四边形ABCD的对角线,当平行四边形 ABCD满足:①∠1=∠2;②∠2=∠3;③∠B=∠3;④∠1=∠3中 的某一条件时,平行四边形ABCD是菱形,这个条件是( ). A.①或② B.②或③ C.③或④ D.①或④ D
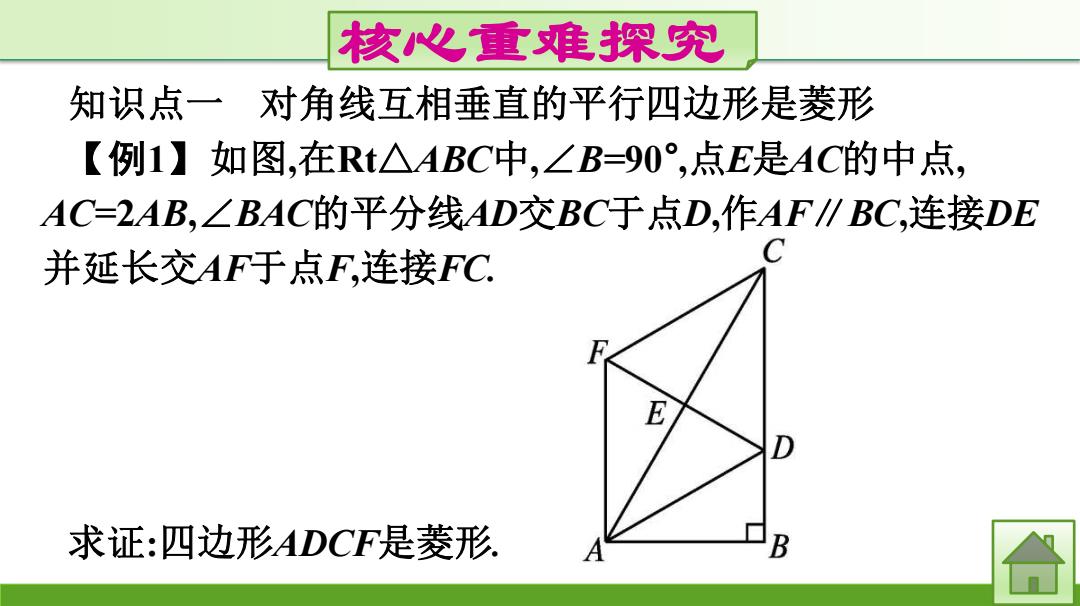
核心重难探究 知识点一对角线互相垂直的平行四边形是菱形 【例1】如图,在Rt△ABC中,∠B=90°,点E是AC的中点, AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE 并延长交AF于点F,连接FC E 求证:四边形ADCF是菱形 A B
核心重难探究 知识点一 对角线互相垂直的平行四边形是菱形 【例1】如图,在Rt△ABC中,∠B=90° ,点E是AC的中点, AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE 并延长交AF于点F,连接FC. 求证:四边形ADCF是菱形

思路点拨:(I)△AEF与△CED全等吗?线段AF与CD是否相 等? (2)四边形ADCF是平行四边形吗?为什么? 3)△AED与△ABD全等吗?∠AED等于多少度? 合
思路点拨:(1)△AEF与△CED全等吗?线段AF与CD是否相 等? (2)四边形ADCF是平行四边形吗?为什么? (3)△AED与△ABD全等吗?∠AED等于多少度?

证明:.AF∥CD, '.∠EAF=∠ECD,∠EFA=∠EDC. 又点E是AC的中点,'.AE=CE, .△AEF2△CED,'.AF=CD. 又AF∥CD,'.四边形ADCF是平行四边形. 在△AED和△ABD中,由题意, 知AE=AB,∠EAD=∠BAD,AD=AD,'.△AED≌△ABD, '.∠AED=∠B=90°,即DF⊥AC. ∴.四边形ADCF是菱形
证明:∵AF∥CD, ∴∠EAF =∠ECD,∠EFA=∠EDC. 又点E是AC的中点,∴AE=CE, ∴△AEF≌△CED,∴AF =CD. 又AF∥CD,∴四边形ADCF是平行四边形. 在△AED和△ABD中,由题意, 知AE=AB,∠EAD=∠BAD,AD=AD,∴△AED≌△ABD, ∴∠AED=∠B=90° ,即DF⊥AC. ∴四边形ADCF是菱形

【方法归纳】 在进行菱形的判定与识别时,要注意它是四边形还是平行四 边形,并根据条件选择合适的判定方法.若是平行四边形,则再 需要下面任一条件,即可判定该平行四边形为菱形:(1)邻边相 等;2)对角线互相垂直;3)每条对角线平分一组对角:
【方法归纳】 在进行菱形的判定与识别时,要注意它是四边形还是平行四 边形,并根据条件选择合适的判定方法.若是平行四边形,则再 需要下面任一条件,即可判定该平行四边形为菱形:(1)邻边相 等;(2)对角线互相垂直;(3)每条对角线平分一组对角

知识点二四条边相等的四边形是菱形 【例2】在△ABC中,M是AC边上的一点,连接BM,将△ABC 沿AC翻折,使点B落在点D处,当DMIIAB时,求证:四边形 ABMD是菱形. M B 合
知识点二 四条边相等的四边形是菱形 【例2】在△ABC中,M是AC边上的一点,连接BM.将△ABC 沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形 ABMD是菱形