
家庭猴亚 第2课时 用公式法求解一元二次方程的实际应用
第2课时 用公式法求解一元二次方程的实际应用

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.一块矩形菜地的面积是120m2,如果它的长减少2m,那么菜 地就变成正方形,原菜地的长是 m. 合
基础自主梳理 1.一块矩形菜地的面积是120 m2 ,如果它的长减少2 m,那么菜 地就变成正方形,原菜地的长是12 m
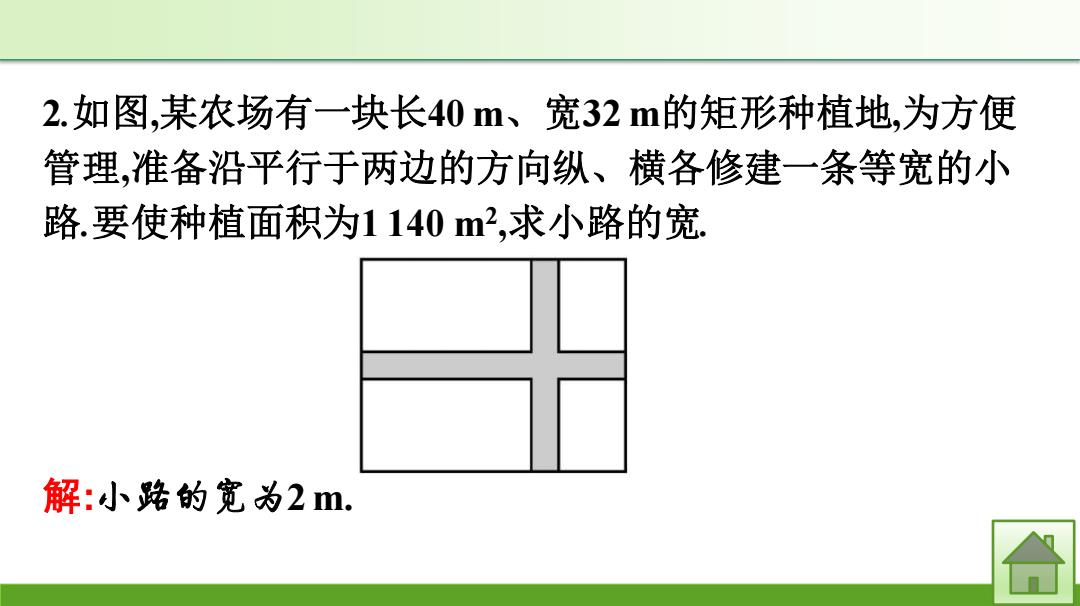
2.如图,某农场有一块长40m、宽32m的矩形种植地,为方便 管理,准备沿平行于两边的方向纵、横各修建一条等宽的小 路.要使种植面积为1140m2,求小路的宽 解:小路的宽为2m
2.如图,某农场有一块长40 m、宽32 m的矩形种植地,为方便 管理,准备沿平行于两边的方向纵、横各修建一条等宽的小 路.要使种植面积为1 140 m2 ,求小路的宽. 解:小路的宽为2 m
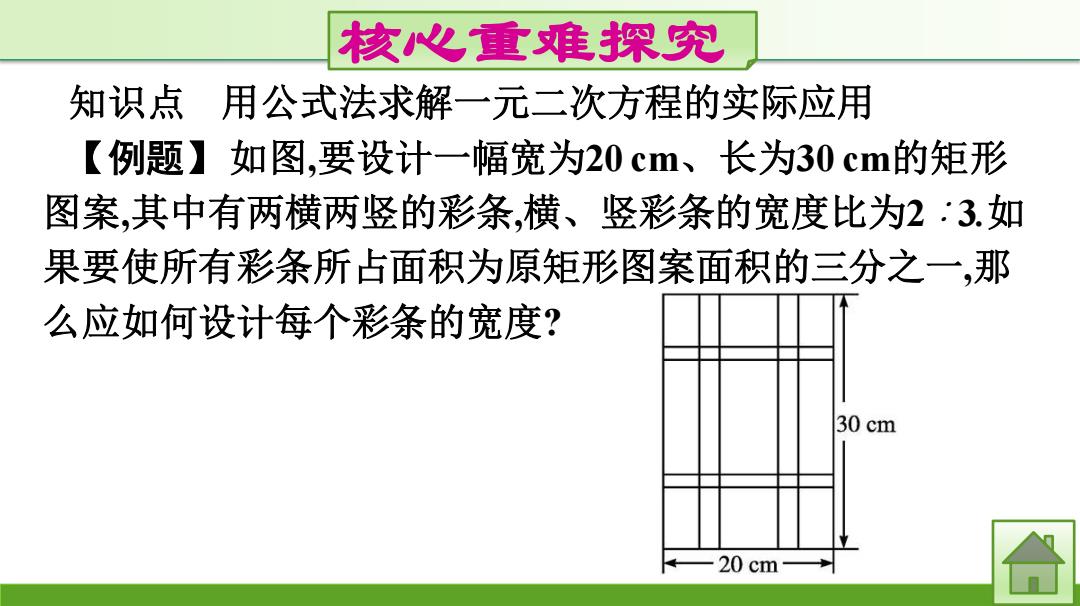
核心重难探究 知识点 用公式法求解一元二次方程的实际应用 【例题】如图,要设计一幅宽为20cm、长为30cm的矩形 图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3.如 果要使所有彩条所占面积为原矩形图案面积的三分之一,那 么应如何设计每个彩条的宽度? 30 cm 20 cm-
核心重难探究 知识点 用公式法求解一元二次方程的实际应用 【例题】如图,要设计一幅宽为20 cm、长为30 cm的矩形 图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3.如 果要使所有彩条所占面积为原矩形图案面积的三分之一,那 么应如何设计每个彩条的宽度?

思路点拨:由横、竖彩条的宽度比为23,可设每个横向彩 条的宽为2xcm,则每个竖向彩条的宽为3xcm.为更好地寻找 题目中的等量关系,将横、竖彩条分别集中,得到矩形ABCD, 如参考答案中的图.用含x的代数式分别表示出AB,AD的长,进 而利用矩形ABCD的面积列出方程求解
思路点拨:由横、竖彩条的宽度比为2∶3,可设每个横向彩 条的宽为2x cm,则每个竖向彩条的宽为3x cm.为更好地寻找 题目中的等量关系,将横、竖彩条分别集中,得到矩形ABCD. 如参考答案中的图.用含x的代数式分别表示出AB,AD的长,进 而利用矩形ABCD的面积列出方程求解

解:如图,设姜个横向彩条的宽为2xcm, 则每个竖向彩条的宽为3xcm, AB=(20-6xcm,AD=(30-4x)cm(0<X<) 30 cm 所以矩形ABCD的面积为 (20-6)30-4)=24x2-260x+600(0<x<9 准装夏生,得24260601)2030 B 20cm- 整理,得6x2-65x+50=0
解:如图,设每个横向彩条的宽为2x cm, 则每个竖向彩条的宽为3x cm, AB=(20-6x)cm,AD=(30-4x)cm 𝟎 < 𝐱 < 𝟏𝟎 𝟑 , 所以矩形 ABCD 的面积为 (20-6x) (30-4x) =24x2 -260x+600 𝟎 < 𝐱 < 𝟏𝟎 𝟑 . 根据题意,得 24x2 -260x+600= 𝟏- 𝟏 𝟑 ×20×30. 整理,得 6x2 -65x+50=0

韩古程,得X65,即宫=10(不合通意,合去) 5 则23-号 故专个授、受彩条的宽度分别为号cm、 m. 合
解方程,得 x= 𝟔𝟓±𝟓𝟓 𝟏𝟐 ,即 x1= 𝟓 𝟔 ,x2=10(不合题意,舍去). 则 2x=𝟓 𝟑 ,3x=𝟓 𝟐 . 故每个横、竖彩条的宽度分别为𝟓 𝟑 cm、 𝟓 𝟐 cm

【方法归纳】 列一元二次方程解答面积问题,一般需用面积公式作为等量 关系来列方程,如何用含未知数的代数式来表示边长,是解答 该类问题的关键所在.如果图形的面积不易直接求出,那么可 以利用“平移法”或“割补法”,将分散的图形集中在一起,组成 一个规则图形后,借助转化思想和整体思想就很容易地列出 方程
【方法归纳】 列一元二次方程解答面积问题,一般需用面积公式作为等量 关系来列方程,如何用含未知数的代数式来表示边长,是解答 该类问题的关键所在.如果图形的面积不易直接求出,那么可 以利用“平移法”或“割补法”,将分散的图形集中在一起,组成 一个规则图形后,借助转化思想和整体思想就很容易地列出 方程
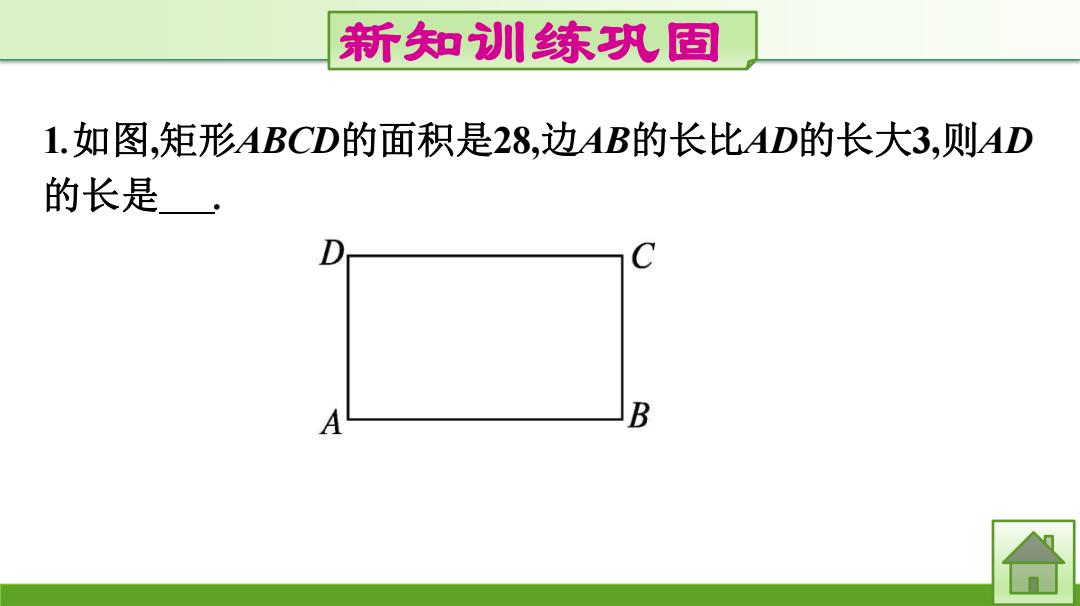
新知训川练织固 1.如图,矩形ABCD的面积是28,边AB的长比AD的长大3,则AD 的长是 A B 合
新知训练巩固 1.如图,矩形ABCD的面积是28,边AB的长比AD的长大3,则AD 的长是4