
家庭值四 3 相似多边形
3 相似多边形

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.各角分别 、各边 的两个多边形叫做相似 多边形 温馨提示 1.若两个多边形相似,则它们的形状相同,但大小不一定相等 2.相似多边形用符号“一”表示,读作“相似于”.如四边形 ABCD与四边形A1B1C1D1相似,记作四边形ABCD~四边形 AB,CD1在记两个多边形相似时,注意要把表示对应顶点的 字母写在对应的位置上
基础自主梳理 1.各角分别相等 、各边成比例 的两个多边形叫做相似 多边形. 温馨提示 1.若两个多边形相似,则它们的形状相同,但大小不一定相等. 2.相似多边形用符号“∽”表示,读作“相似于” .如四边形 ABCD与四边形A1B1C1D1相似,记作四边形ABCD∽四边形 A1B1C1D1 .在记两个多边形相似时,注意要把表示对应顶点的 字母写在对应的位置上

2.相似多边形 叫做相似比. 名师指导 1.两个全等的多边形一定是相似多边形,即全等是相似的特 殊情况,此时其相似比为1. 2.说相似比时,一定要注意顺序,如果△ABC和△A'B'C相似, 其相似比为1:3,那么△A'B'C和△ABC的相似比为3:1
2.相似多边形对应边的比 叫做相似比. 名师指导 1.两个全等的多边形一定是相似多边形,即全等是相似的特 殊情况,此时其相似比为1. 2.说相似比时,一定要注意顺序,如果△ABC和△A'B'C'相似, 其相似比为1∶3,那么△A'B'C'和△ABC的相似比为3∶1

3.下列四组图形中,一定相似的是(D) A.任意两个矩形 B.正方形与菱形 C.任意两个菱形 D.任意两个正五边形
3.下列四组图形中,一定相似的是( ). A.任意两个矩形 B.正方形与菱形 C.任意两个菱形 D.任意两个正五边形 D
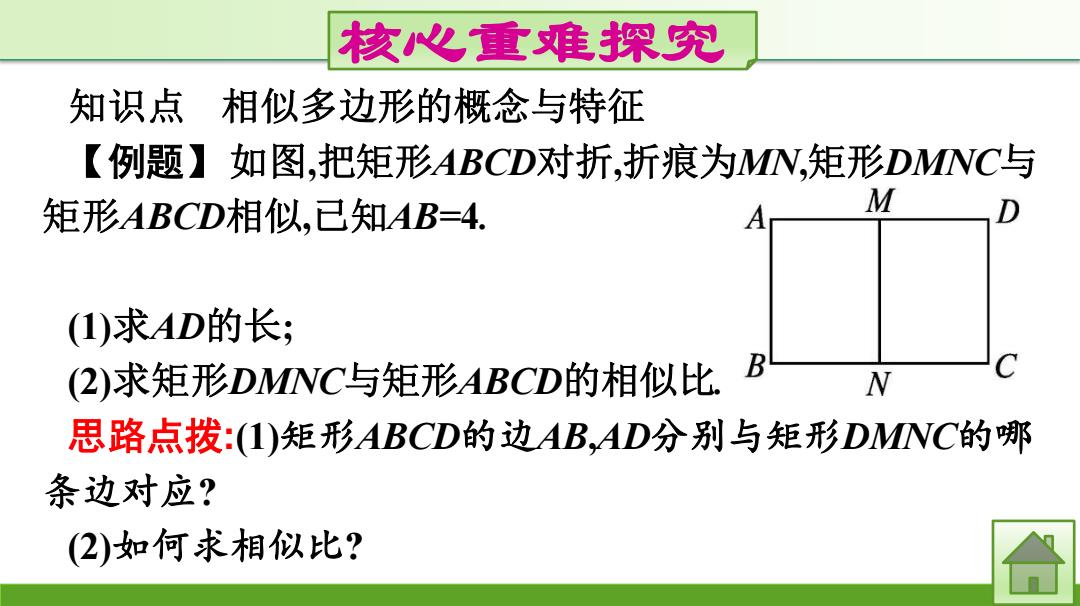
核心重难探究 知识点 相似多边形的概念与特征 【例题】如图,把矩形ABCD对折,折痕为MN,矩形DMNC与 矩形ABCD相似,已知AB=4. M ()求AD的长; (2)求矩形DMNC与矩形ABCD的相似比 B W C 思路点拨:(1)矩形ABCD的边AB,AD分别与矩形DMNC的哪 条边对应? 2)如何求相似比?
核心重难探究 知识点 相似多边形的概念与特征 【例题】如图,把矩形ABCD对折,折痕为MN,矩形DMNC与 矩形ABCD相似,已知AB=4. (1)求AD的长; (2)求矩形DMNC与矩形ABCD的相似比. 思路点拨:(1)矩形ABCD的边AB,AD分别与矩形DMNC的哪 条边对应? (2)如何求相似比?

解:()由己知,得MIN=AB-=4,MD-AD. .'矩形DNC与矩形ABCD相似, ·DM MN DC AB BC 又MIN=DC ∴2AD2=16,AD=4V2. (2)矩形DMNC与矩形ABCD的相似比为 DM = 2V2 = AB 4 2 合
解:(1)由已知,得 MN=AB=4,MD=𝟏 𝟐 AD. ∵矩形 DMNC 与矩形 ABCD 相似, ∴ 𝐃𝐌 𝐀𝐁 = 𝐌𝐍 𝐁𝐂 = 𝐃𝐂 𝐀𝐃 ,又 MN=DC, ∴ 𝟏 𝟐 AD2 =16,∴AD=4 𝟐. (2)矩形 DMNC 与矩形 ABCD 的相似比为 𝐃𝐌 𝐀𝐁 = 𝟐 𝟐 𝟒 = 𝟐 𝟐

【方法归纳】 相似多边形的概念具有判定和性质双重功能,判断两个多边 形相似必须同时具备三个条件:边数相同;对应角相等;对应边 成比例缺一不可.相似多边形的性质通常用来求两个相似多 边形中未知的边、角的大小,或相似比
【方法归纳】 相似多边形的概念具有判定和性质双重功能,判断两个多边 形相似必须同时具备三个条件:边数相同;对应角相等;对应边 成比例.缺一不可.相似多边形的性质通常用来求两个相似多 边形中未知的边、角的大小,或相似比

新知训训练织固 1.用一个4倍放大镜照△ABC,下列说法错误的是(A). A.△ABC放大后,∠B是原来的4倍 B.△ABC放大后,边AB是原来的4倍 C.△ABC放大后,周长是原来的4倍 D.△ABC放大后,面积是原来的16倍 2.己知矩形ABCD与矩形AB'CD'相似,它们的周长分别为80 cm和64cm,若矩形ABCD的宽AB=10cm,则矩形A'B'CD的 宽AB'=
新知训练巩固 1.用一个4倍放大镜照△ABC,下列说法错误的是( ). A.△ABC放大后,∠B是原来的4倍 B.△ABC放大后,边AB是原来的4倍 C.△ABC放大后,周长是原来的4倍 D.△ABC放大后,面积是原来的16倍 2.已知矩形ABCD与矩形A'B'C'D'相似,它们的周长分别为80 cm和64 cm,若矩形ABCD的宽AB=10 cm,则矩形A'B'C'D'的 宽A'B'=8 cm . A
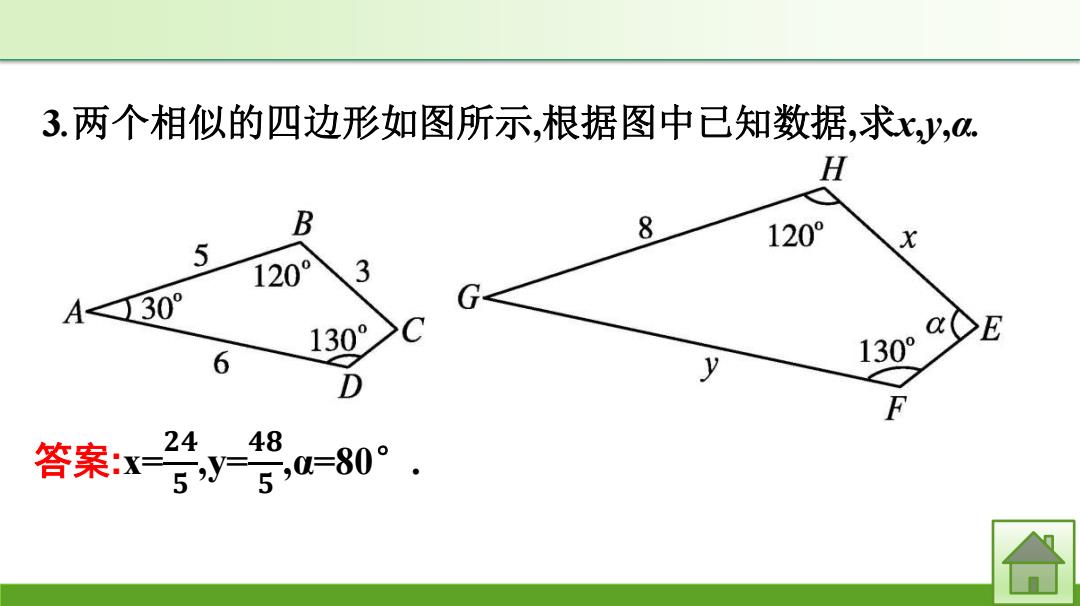
3.两个相似的四边形如图所示,根据图中已知数据,求xy,α H B 8 120° 5 120° 3 A130° G 130 6 130cE D 答案x 244 5,0=80°
3.两个相似的四边形如图所示,根据图中已知数据,求x,y,α. 答案:x= 𝟐𝟒 𝟓 ,y= 𝟒𝟖 𝟓 ,α=80°