
家庭猴伞 第2课时 相以三角形周长比与面积比的性质
第2课时 相似三角形周长比与面积比的性质

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.相似三角形的性质定理 相似三角形的周长比等于 ,面积比等于 名师指导 相似三角形的性质,揭示的是它们的对应线段、周长、面积 与相似比的关系,在解决相似三角形的问题时要灵活运用,并 加以区分,不能混淆!
基础自主梳理 1.相似三角形的性质定理 相似三角形的周长比等于相似比 ,面积比等于相似比的平方 . 名师指导 相似三角形的性质,揭示的是它们的对应线段、周长、面积 与相似比的关系,在解决相似三角形的问题时要灵活运用,并 加以区分,不能混淆
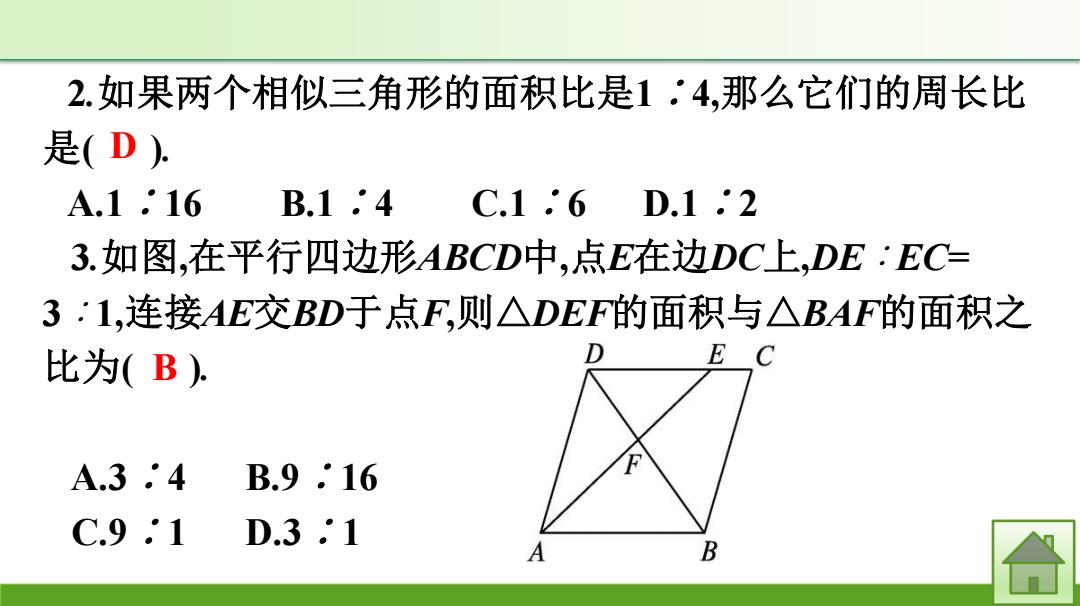
2.如果两个相似三角形的面积比是1.'4,那么它们的周长比 是(D) A.116 B.14 C.1.6 D.1.2 3.如图,在平行四边形ABCD中,点E在边DC上,DE:EC= 3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之 比为(B) E A.3.4 B.9.16 C.9.1 D.3.1 A B
2.如果两个相似三角形的面积比是1∶4,那么它们的周长比 是( ). A.1∶16 B.1∶4 C.1∶6 D.1∶2 3.如图,在平行四边形ABCD中,点E在边DC上,DE∶EC= 3∶1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之 比为( ). A.3∶4 B.9∶16 C.9∶1 D.3∶1 D B
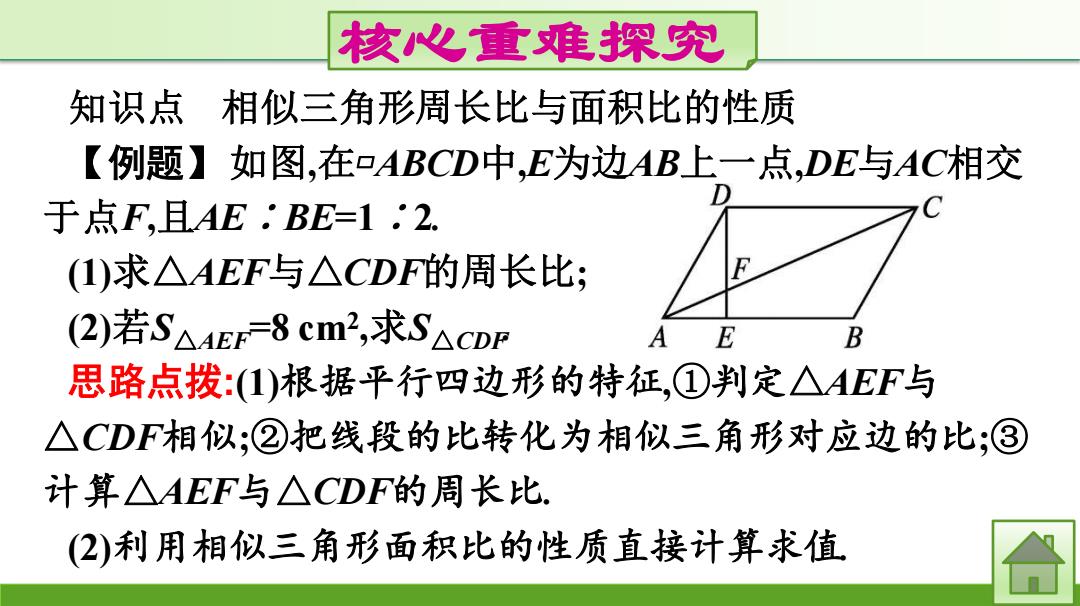
核心重难探究 知识点 相似三角形周长比与面积比的性质 【例题】如图,在-ABCD中,E为边AB上一点,DE与AC相交 于点F,且AE.BE=12. (1)求△AEF与△CDF的周长比; (2)若S△4Ep=8cm2,求S△cDr E B 思路点拨:1)根据平行四边形的特征,①判定△AEF与 △CDF相似;②把线段的比转化为相似三角形对应边的比;③ 计算△AEF与△CDF的周长比. 2)利用相似三角形面积比的性质直接计算求值
核心重难探究 知识点 相似三角形周长比与面积比的性质 【例题】如图,在▱ABCD中,E为边AB上一点,DE与AC相交 于点F,且AE∶BE=1∶2. (1)求△AEF与△CDF的周长比; (2)若S△AEF =8 cm2 ,求S△CDF. 思路点拨:(1)根据平行四边形的特征,①判定△AEF与 △CDF相似;②把线段的比转化为相似三角形对应边的比;③ 计算△AEF与△CDF的周长比. (2)利用相似三角形面积比的性质直接计算求值

解:1).AE:BE=1:2,∴.AE:AB=1:3. 由平行四边形的性质,得AB=CD,AB∥CD. '.有AE:CD=1:3,△AEF∽△CDF. .△AEF与△CDF周长比为1:3. (2)△AEF∽△CDF,.S△AEF:S△CD=1:9. ∴.S△cDp-9X8=72(cm2)
解:(1)∵AE∶BE=1∶2,∴AE∶AB=1∶3. 由平行四边形的性质,得AB=CD,AB∥CD. ∴有AE∶CD=1∶3,△AEF∽△CDF. ∴△AEF与△CDF周长比为1∶3. (2)∵△AEF∽△CDF,∴S△AEF∶S△CDF=1∶9. ∴S△CDF=9×8=72(cm2 )

【方法归纳】 1.计算相似三角形的周长比、面积比时,要正确运用性质结 论,不要混淆,同时还要注意两个三角形的先后顺序,注意找准 对应线段 2.遇到面积关系问题时,若两三角形相似,则面积比等于相似 比的平方;若两三角形不相似但等底(或等高),则它们的面积 比等于高(或底)之比
【方法归纳】 1.计算相似三角形的周长比、面积比时,要正确运用性质结 论,不要混淆,同时还要注意两个三角形的先后顺序,注意找准 对应线段. 2.遇到面积关系问题时,若两三角形相似,则面积比等于相似 比的平方;若两三角形不相似但等底(或等高),则它们的面积 比等于高(或底)之比
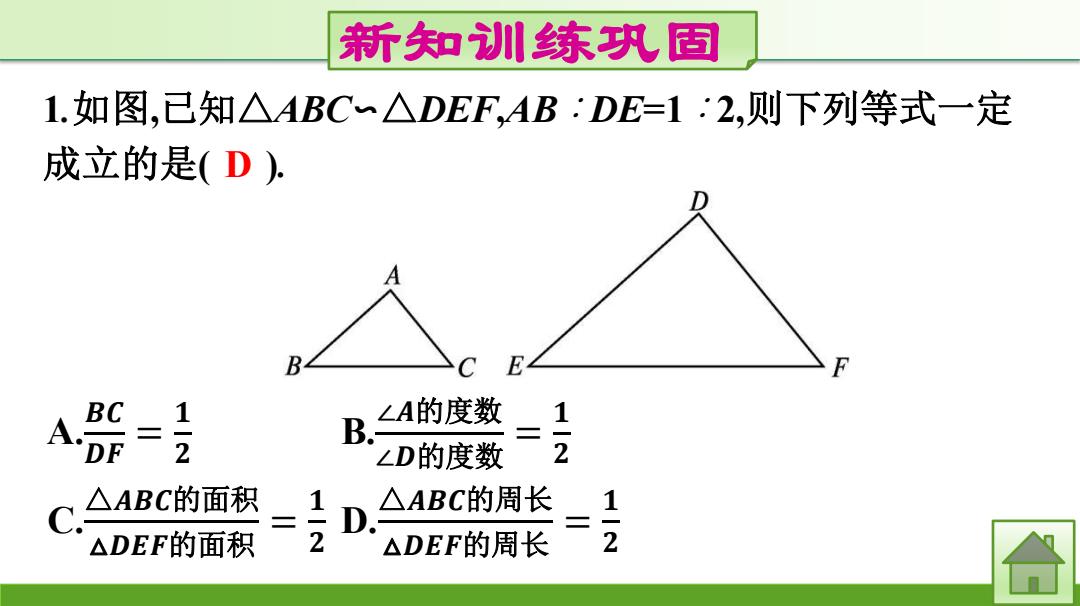
新知训练织固 1.如图,已知△ABC△DEF,ABDE=1:2,则下列等式一定 成立的是(D) B C E BC 1 A的度数 1 DF B. D的度数 -2 C △ABC的面积 = D. △ABC的周长 1 △DEF的面积 2 △DEF的周长 -2
新知训练巩固 1.如图,已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定 成立的是( ). A. 𝑩𝑪 𝑫𝑭 = 𝟏 𝟐 B. ∠𝑨的度数 ∠𝑫的度数 = 𝟏 𝟐 C. △𝑨𝑩𝑪的面积 △𝑫𝑬𝑭的面积 = 𝟏 𝟐 D. △𝑨𝑩𝑪的周长 △𝑫𝑬𝑭的周长 = 𝟏 𝟐 D

2.已知△ABC~△DEF,相似比为2,且△ABC的面积为16,则 △DEF的面积为(C), A.32 B.8 C.4 D.16 3.如图,在△ABC中,D,E分别是边AB,AC上的点,且DEII BC,若 △ADE与△ABC的周长之比为2:3,AD=4,则DB= D E B
2.已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则 △DEF的面积为( ). A.32 B.8 C.4 D.16 3.如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,若 △ADE与△ABC的周长之比为2∶3,AD=4,则DB=2 . C
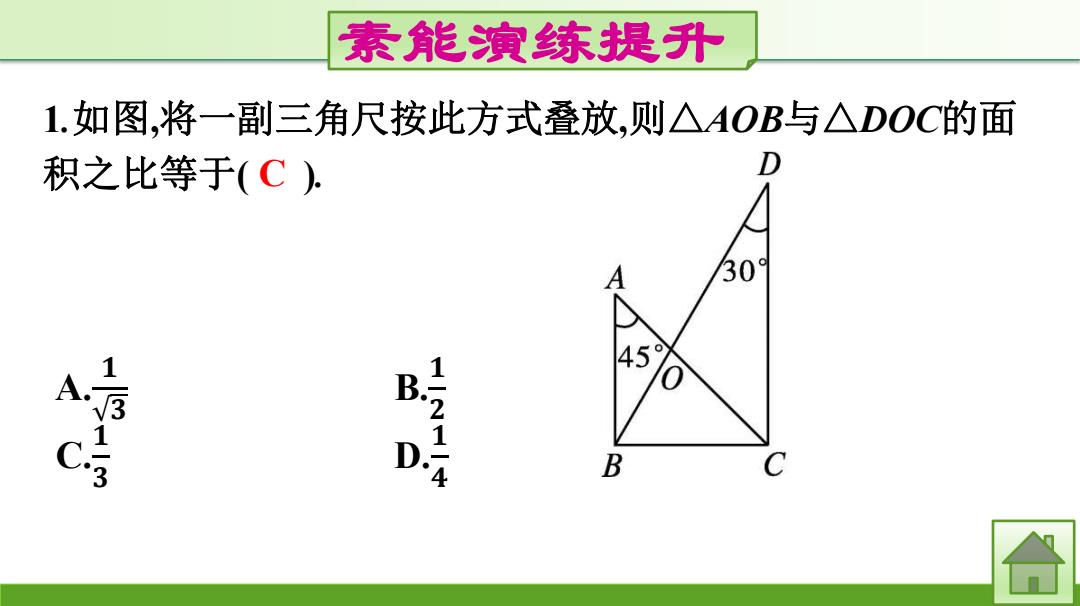
素能演练提升 1.如图,将一副三角尺按此方式叠放,则△AOB与△DOC的面 积之比等于(C). 309 45 2,μN B B 合
素能演练提升 1.如图,将一副三角尺按此方式叠放,则△AOB与△DOC的面 积之比等于( C ). A. 𝟏 𝟑 B. 𝟏 𝟐 C. 𝟏 𝟑 D. 𝟏 𝟒