
家庭馆业 第一章 直确三角形的边角关系 230°,45°,60°角的三角函数值
第一章 直角三角形的边角关系 2 30°,45°,60°角的三角函数值

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
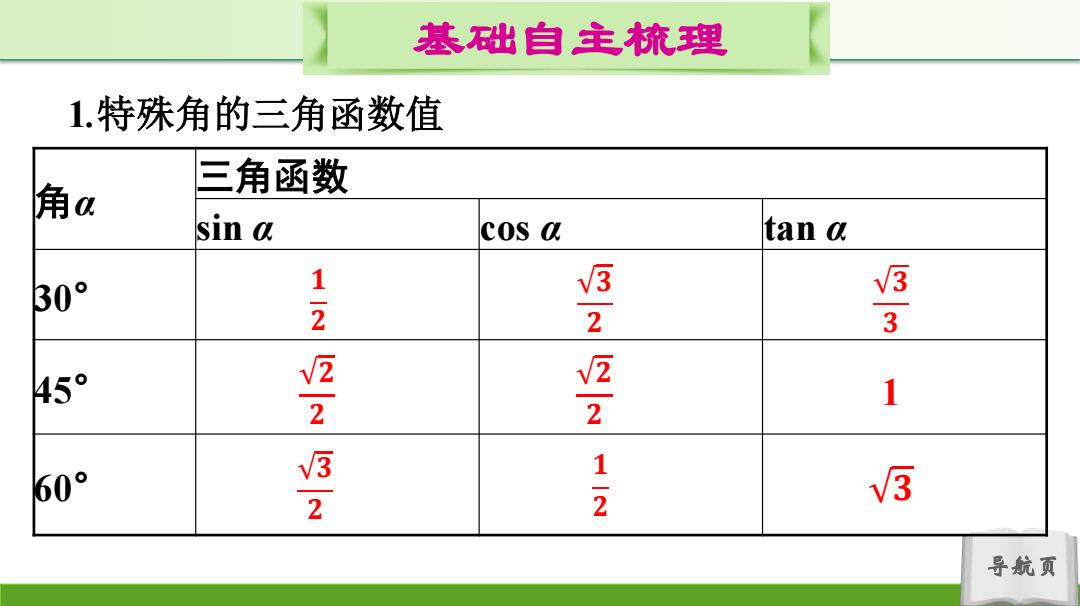
基础自主梳理 1.特殊角的三角函数值 三角函数 角a sin a cos a tan a 30° 1-2 3 3 3 45 √2 2 2 1 60° 2 1-2 3 导航页
导航页 基础自主梳理 1.特殊角的三角函数值 角α 三角函数 sin α cos α tan α 30° 45° 60° 𝟏 𝟐 𝟑 𝟐 𝟑 𝟑 𝟐 𝟐 𝟐 𝟐 1 𝟑 𝟐 𝟏 𝟐 𝟑

基础自主梳理 温馨提示 1.记忆特殊角的三角函数值可以采用如下的方法: (1)图形记忆法:根据特殊角所在的直角三角形记忆 (2)列表记忆法:如上表所示. (3)规律记忆法:30°,45°,60°角的三角函数值中,正弦值和余 弦值的分母都是2,正切值的分母是3,它们分子的被开方数可 简记为:1,2,3;3,2,13,9,27. 导航页
导航页 基础自主梳理 温馨提示 1.记忆特殊角的三角函数值可以采用如下的方法: (1)图形记忆法:根据特殊角所在的直角三角形记忆. (2)列表记忆法:如上表所示. (3)规律记忆法:30°,45°,60°角的三角函数值中,正弦值和余 弦值的分母都是2,正切值的分母是3,它们分子的被开方数可 简记为:1,2,3;3,2,1;3,9,27

基础自主梳理 2.当锐角α的度数逐渐增大时,正弦值和正切值随之逐渐增 大,而余弦值随之逐渐减小 3.通过该表可以方便地知道30°,45°,60°角的各三角函数值; 同样地,如果知道了一个锐角的三角函数值,那么也可以求出 这个锐角的度数 导航页
导航页 基础自主梳理 2.当锐角α的度数逐渐增大时,正弦值和正切值随之逐渐增 大,而余弦值随之逐渐减小. 3.通过该表可以方便地知道30°,45°,60°角的各三角函数值; 同样地,如果知道了一个锐角的三角函数值,那么也可以求出 这个锐角的度数
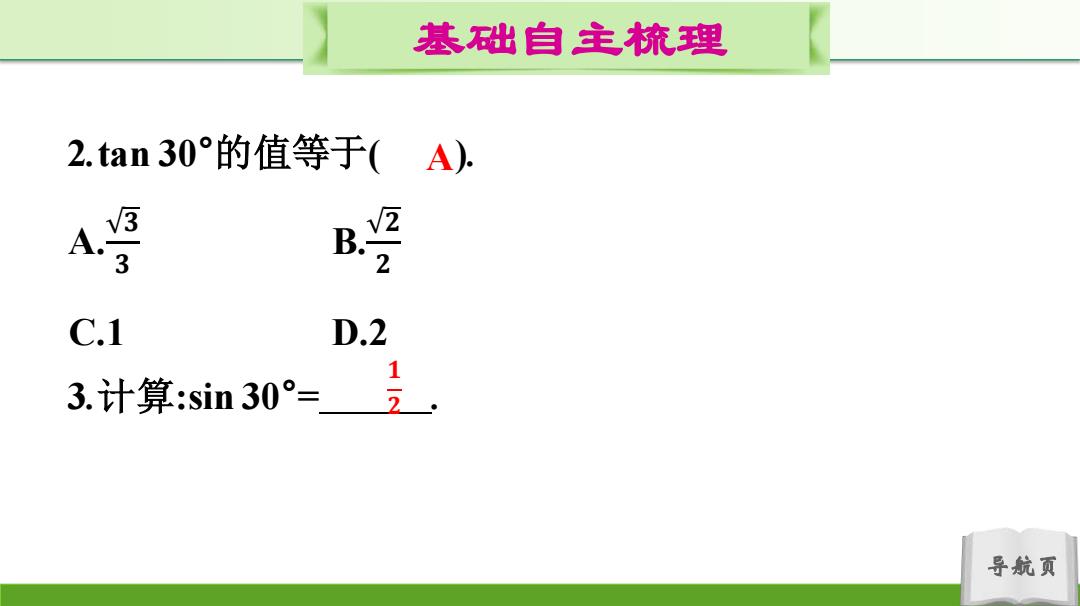
基础自主梳理 2.tan30°的值等于(A) B C.1 D.2 1 3.计算:sin30°= 导航页
导航页 基础自主梳理 2.tan 30°的值等于( ). A. 𝟑 𝟑 B. 𝟐 𝟐 C.1 D.2 3.计算:sin 30° = . A 𝟏 𝟐
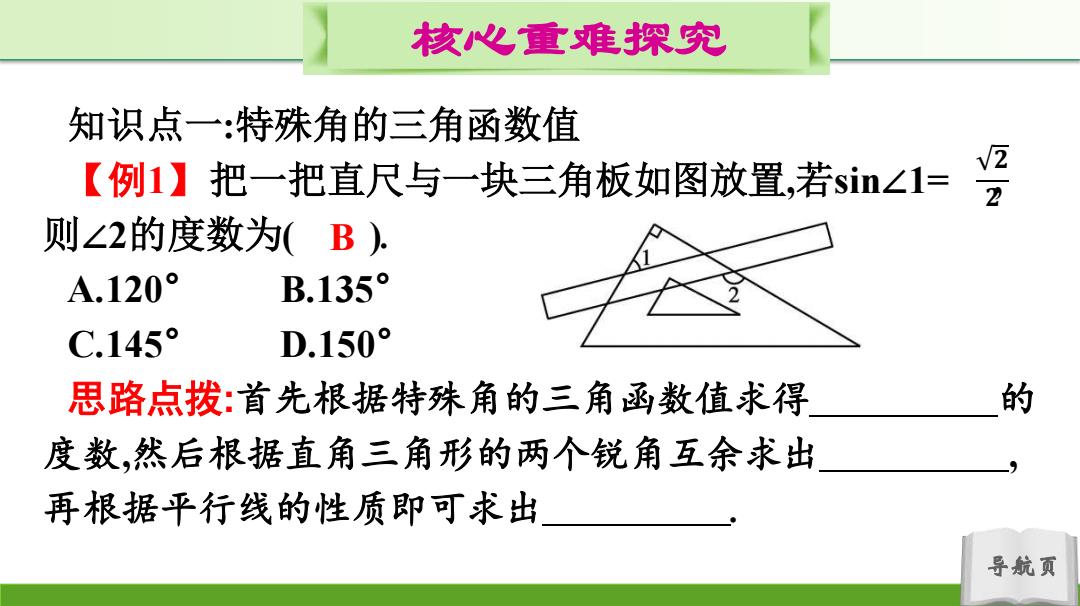
核心重难探究 知识点一:特殊角的三角函数值 【例1】把一把直尺与一块三角板如图放置,若sin∠1= 则∠2的度数为(B) A.120° B.135° C.145° D.150° 思路点拨:首先根据特殊角的三角函数值求得 的 度数,然后根据直角三角形的两个锐角互余求出 再根据平行线的性质即可求出 导航页
导航页 核心重难探究 知识点一:特殊角的三角函数值 【例1】把一把直尺与一块三角板如图放置,若sin∠1= , 则∠2的度数为( ). A.120° B.135° C.145° D.150° 思路点拨:首先根据特殊角的三角函数值求得 的 度数,然后根据直角三角形的两个锐角互余求出 , 再根据平行线的性质即可求出 . 𝟐 𝟐 B

核心重难探究 【方法归纳】 解决这类问题要注意数形结合,正确运用特殊角的三角函数 值、直角三角形的性质、平行线的性质求解即可. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题要注意数形结合,正确运用特殊角的三角函数 值、直角三角形的性质、平行线的性质求解即可
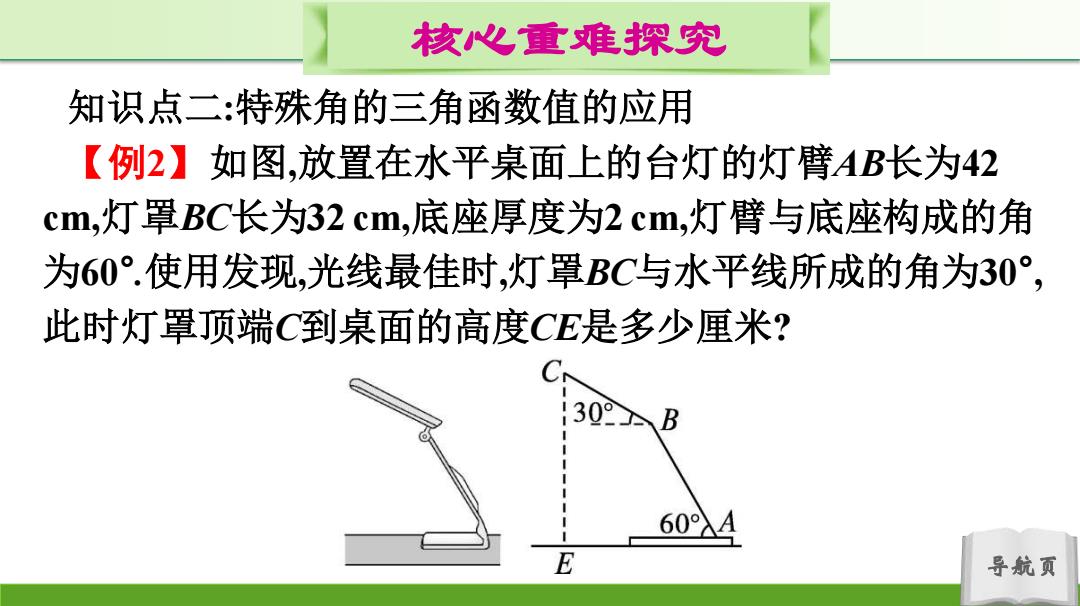
核心重难探究 知识点二:特殊角的三角函数值的应用 【例2】如图,放置在水平桌面上的台灯的灯臂AB长为42 cm,灯罩BC长为32cm,底座厚度为2cm,灯臂与底座构成的角 为60°.使用发现,光线最佳时,灯罩BC与水平线所成的角为30°, 此时灯罩顶端C到桌面的高度CE是多少厘米? 130 B 60A E 导航页
导航页 核心重难探究 知识点二:特殊角的三角函数值的应用 【例2】如图,放置在水平桌面上的台灯的灯臂AB长为42 cm,灯罩BC长为32 cm,底座厚度为2 cm,灯臂与底座构成的角 为60° .使用发现,光线最佳时,灯罩BC与水平线所成的角为30° , 此时灯罩顶端C到桌面的高度CE是多少厘米?

核心重难探究 思路点拨:作AD⊥CE,BM⊥CE,BF⊥AD.根据sin∠CBM =sin30°= ,求出CM的长,根据sin∠BAF=sin60° 三 ,求出BF的长,得出 的长,即可得出CE 的长 导航页
导航页 核心重难探究 思路点拨:作AD⊥CE,BM⊥CE,BF⊥AD.根据sin∠CBM =sin 30° = ,求出CM的长,根据sin∠BAF=sin 60° = ,求出BF的长,得出 的长,即可得出CE 的长