
家庭值亚 5 二次数与一元二次方程 第2课时 利用二次函数的图象估计一元二次方程的根
5 二次函数与一元二次方程 第2课时 利用二次函数的图象估计一元二次方程的根

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.用图象法求一元二次方程(ax2+bx+c-0)的近似根的一般步 骤: (1)作出函数的图象,并由图象确定方程的解的个数; (2)由图象与x轴的交点位置确定交点横坐标的范围; (3)利用计算器进行探索,估算方程的近似根 2.用图象法求一元二次方程的近似根时,结果只取到十分位 导航页
导航页 基础自主梳理 1.用图象法求一元二次方程(ax2+bx+c=0)的近似根的一般步 骤: (1)作出函数的图象,并由图象确定方程的解的 ; (2)由图象与x轴的交点位置确定交点横坐标的范围; (3)利用计算器进行探索,估算方程的近似根. 2.用图象法求一元二次方程的近似根时,结果只取到 位. 个数 十分

基础自主梳理 温馨提示 求一元二次方程x2+bx+c=0的近似解常用方法有以下三种: (1)直接作二次函数y=x2+bx+c的图象,抛物线与x轴交,点的横坐 标就是对应一元二次方程2+bx+c=的根 (2)先将一元二次方程x2+bx+c=0变为x2+bx=-C,再分别作抛物 线y=2+bx和直线y=-C,则直线y三c与抛物线交点的横坐标就是对 应一元二次方程x2+bx+c=0的根 (3)先将一元二次方程x2+bx+c=0变为x2=-bx-c,再分别作抛物 线y=x2和直线y=-bx-C,则两函数图象交点的横坐标就是对应一元 二次方程x2+bx+c=0的根. 导航页
导航页 基础自主梳理 温馨提示 求一元二次方程ax2+bx+c=0的近似解常用方法有以下三种: (1)直接作二次函数y=ax2+bx+c的图象,抛物线与x轴交点的横坐 标就是对应一元二次方程ax2+bx+c=0的根. (2)先将一元二次方程ax2+bx+c=0变为ax2+bx=-c,再分别作抛物 线y=ax2+bx和直线y=-c,则直线y=-c与抛物线交点的横坐标就是对 应一元二次方程ax2+bx+c=0的根. (3)先将一元二次方程ax2+bx+c=0变为ax2=-bx-c,再分别作抛物 线y=ax2和直线y=-bx-c,则两函数图象交点的横坐标就是对应一元 二次方程ax2+bx+c=0的根
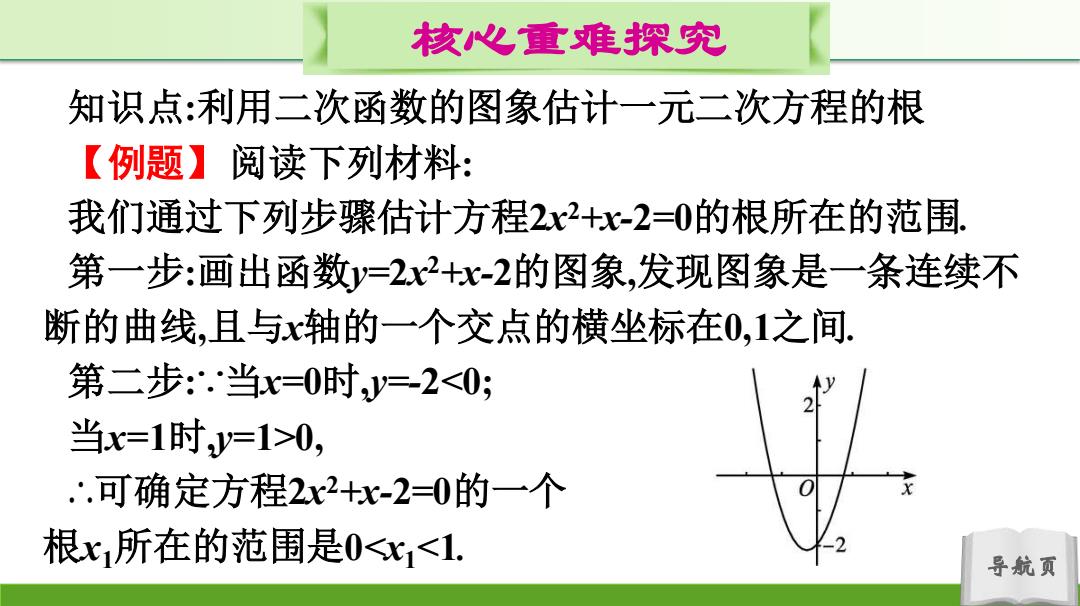
核心重难探究 知识点:利用二次函数的图象估计一元二次方程的根 【例题】阅读下列材料: 我们通过下列步骤估计方程2x2+x-2=0的根所在的范围. 第一步:画出函数y=2x2+x-2的图象,发现图象是一条连续不 断的曲线,且与x轴的一个交点的横坐标在0,1之间. 第二步:.当x=0时y=-20, .可确定方程2x2+x-2=0的一个 根x所在的范围是0<1<1. 导航页
导航页 核心重难探究 知识点:利用二次函数的图象估计一元二次方程的根 【例题】阅读下列材料: 我们通过下列步骤估计方程2x 2+x-2=0的根所在的范围. 第一步:画出函数y=2x 2+x-2的图象,发现图象是一条连续不 断的曲线,且与x轴的一个交点的横坐标在0,1之间. 第二步:∵当x=0时,y=-20, ∴可确定方程2x 2+x-2=0的一个 根x1所在的范围是0<x1<1

核心重难探究 第三步:通过取0和1的平均数缩小x所在的范围; 取=当号时 当x=1时>0,1<1. 2 (1)请仿照第二步,通过运算,验证2x2+x-2=0的另一个根x2所 在范围是-2<x2<-1; (2)在-2<x2<-1的基础上,重复应用第三步中取平均数的方法, 将x,所在范围缩小至<x,<n,使得n-m≤. 导航页
导航页 核心重难探究 第三步:通过取0和1的平均数缩小x1所在的范围; 取 x= 𝟎+𝟏 𝟐 = 𝟏 𝟐 ,∵当 x= 𝟏 𝟐 时,y0,∴ 𝟏 𝟐 <x1<1. (1)请仿照第二步,通过运算,验证2x 2+x-2=0的另一个根x2所 在范围是-2<x2<-1; (2)在-2<x2<-1的基础上,重复应用第三步中取平均数的方法, 将x2所在范围缩小至m<x2<n,使得n-m≤ . 𝟏 𝟒
核心重难探究 思路点拨:1)计算x= 和x= 时y的值,确定 x2所在范围是-2<x2<-1; (2)先根据第三步-2和-1的平均数确定x= ,计算= 时y的值,得 <x2<-1;同理再求-1和 的 平均数为■ ,计算= 时y的值,从而得出结论. 导航页
导航页 核心重难探究 思路点拨:(1)计算x= 和x= 时,y的值,确定 x2所在范围是-2<x2<-1; (2)先根据第三步-2和-1的平均数确定x= ,计算x= 时y的值,得 <x2<-1;同理再求-1和 的 平均数为 ,计算x= 时y的值,从而得出结论

核心重难探究 解:(1).当=2时y>0; 当x=1时y<0; ∴.方程2x2+x-2=0的另一个根x2所在的范围是-2<x2<-1. 2取20-2 22 :当x时-2x足-22=10: 当x=-1时y=1<0; 导航页
导航页 核心重难探究 解:(1)∵当x=-2时,y>0; 当x=-1时,y0; 当 x=-1 时,y=-1<0; ∴- 𝟑 𝟐 <x2<-1

核心重难探究 取是5 2 :当x时22-2-日0 4 3 当x=时y>0 2 。 3 5 2 2< 4 -()= 三<即为所求的范围 导航页
导航页 核心重难探究 取 x= - 𝟑 𝟐 +(-𝟏) 𝟐 =- 𝟓 𝟒 , ∵当 x=- 𝟓 𝟒 时,y=2× 𝟐𝟓 𝟏𝟔 − 𝟓 𝟒 -2=- 𝟏 𝟖 0; ∴- 𝟑 𝟐 <x2<- 𝟓 𝟒 . 又- 𝟓 𝟒 − - 𝟑 𝟐 = 𝟏 𝟒 , ∴- 𝟑 𝟐 <x2<- 𝟓 𝟒 即为所求 x2的范围

核心重难探究 【方法归纳】 在解题时注意对题目中所给知识的正确理解,仿照阅读材料 提供的方法,运用类比的数学思想,数形结合的数学思想求解, 导航页
导航页 核心重难探究 【方法归纳】 在解题时注意对题目中所给知识的正确理解,仿照阅读材料 提供的方法,运用类比的数学思想,数形结合的数学思想求解