
家庭值四 第三章 :圆 2圆的对称性
第三章 圆 2 圆的对称性

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.圆是轴对称图形,其对称轴是任意一条过圆心 的直 线 2.圆是中心对称图形,对称中心为圆心 温馨提示 1.圆的对称轴有无数条:圆的对称轴是直径所在的直线,而不 是直径 2.圆是一个旋转对称图形,无论绕圆心旋转多少度,它都与自 身重合,其旋转对称中心为圆心 导航页
导航页 基础自主梳理 1.圆是轴对称图形,其对称轴是任意一条过 的直 线. 2.圆是中心对称图形,对称中心为 . 温馨提示 1.圆的对称轴有无数条;圆的对称轴是直径所在的直线,而不 是直径. 2.圆是一个旋转对称图形,无论绕圆心旋转多少度,它都与自 身重合,其旋转对称中心为圆心. 圆心 圆心

基础自主梳理 3.在同圆或等圆中,相等的圆心角所对的 孤 相等,所 对的弦· 也相等 4.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有 一组 量相等,那么它们所对应的其余 各组量都 分别相等 导航页
导航页 基础自主梳理 3.在同圆或等圆中,相等的圆心角所对的 相等,所 对的 也相等. 4.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有 量相等,那么它们所对应的 各组量都 分别相等. 弧 弦 一组 其余

基础自主梳理 温馨提示 1.利用圆心角、孤、弦之间的关系定理要注意,不能忽略 “在同圆或等圆中”这个前提条件,离开这个前提,虽然圆心角 相等,但所对应的孤、弦不一定分别相等. 2.在同圆或等圆中,圆心角相等台孤相等台弦相等台弦心距 相等. 导航页
导航页 基础自主梳理 温馨提示 1.利用圆心角、弧、弦之间的关系定理要注意,不能忽略 “在同圆或等圆中”这个前提条件,离开这个前提,虽然圆心角 相等,但所对应的弧、弦不一定分别相等. 2.在同圆或等圆中,圆心角相等⇔弧相等⇔弦相等⇔弦心距 相等
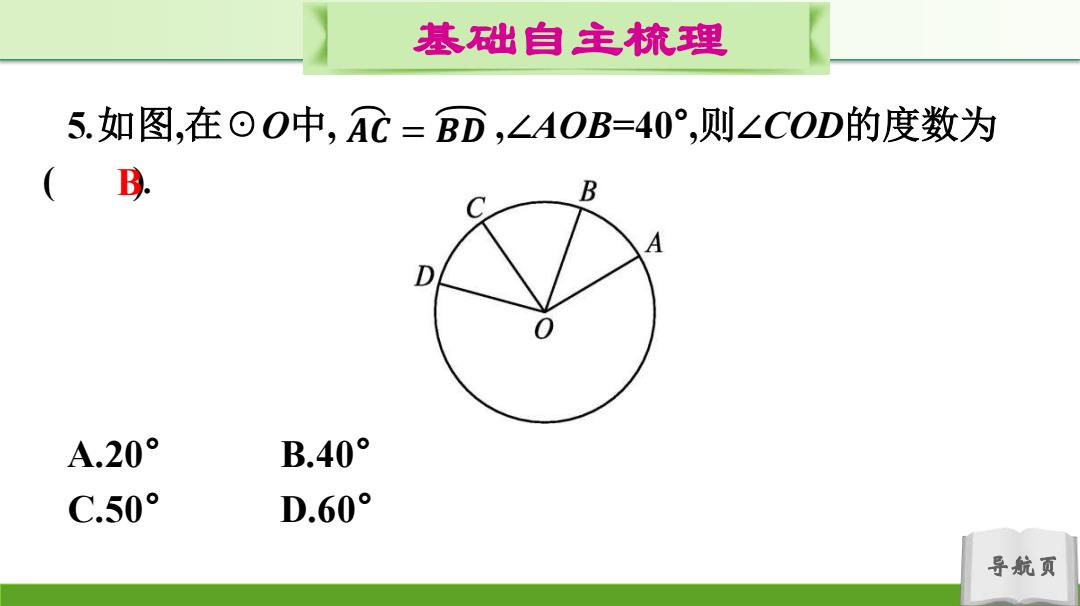
基础自主梳理 5.如图,在⊙O中,C=BD,∠AOB=40°,则∠COD的度数为 B. B A.20° B.40° C.50° D.60° 导航页
导航页 基础自主梳理 5.如图,在☉O中, ,∠AOB=40° ,则∠COD的度数为 ( ). A.20° B.40° C.50° D.60° 𝑨 𝑪 = 𝑩 𝑫 B

核心重难探究 知识点一:圆的对称性 【例1】下列说法中,不正确的是(B)· A.圆是轴对称图形,有无数条对称轴 B.圆是中心对称图形,有无数个对称中心 C.圆的任意一条直径所在直线都是圆的对称轴 D.圆既是轴对称图形又是中心对称图形 思路点拨:分别根据 对称图形和 对称 图形的概念并结合圆的特点判断各选项,然后求解即可. 导航页
导航页 核心重难探究 知识点一:圆的对称性 【例1】下列说法中,不正确的是( ). A.圆是轴对称图形,有无数条对称轴 B.圆是中心对称图形,有无数个对称中心 C.圆的任意一条直径所在直线都是圆的对称轴 D.圆既是轴对称图形又是中心对称图形 思路点拨:分别根据 对称图形和 对称 图形的概念并结合圆的特点判断各选项,然后求解即可. B

核心重难探究 【方法归纳】 解决这类问题关键是掌握好中心对称图形与轴对称图形的 概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可 重合,中心对称图形是要寻找对称中心,图形旋转180°后与原 图重合 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题关键是掌握好中心对称图形与轴对称图形的 概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可 重合,中心对称图形是要寻找对称中心,图形旋转180°后与原 图重合
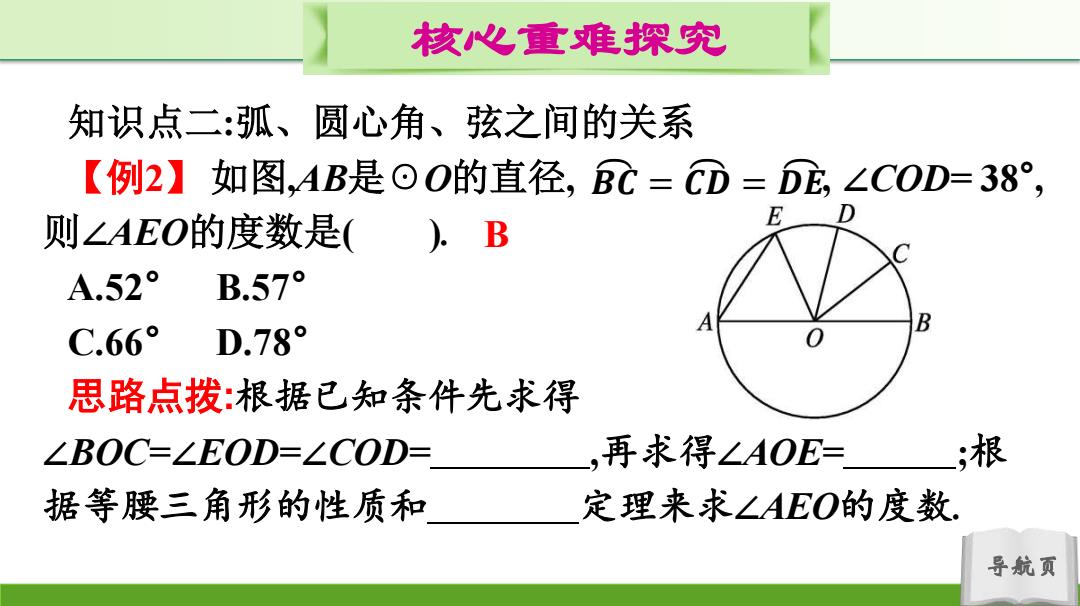
核心重难探究 知识点二:弧、圆心角、弦之间的关系 【例2】如图,AB是⊙O的直径,BC=CD=E,∠COD=38°, 则∠AEO的度数是( E ).B A.52° B.57° B C.66° D.78° 思路点拨:根据已知条件先求得 ∠BOC=∠EOD=∠COD= ,再求得∠AOE= ;根 据等腰三角形的性质和 定理来求∠AEO的度数, 导航页
导航页 核心重难探究 知识点二:弧、圆心角、弦之间的关系 【例2】 如图,AB是☉O的直径, , ∠COD= 38° , 则∠AEO的度数是( ). A.52° B.57° C.66° D.78° 思路点拨:根据已知条件先求得 ∠BOC=∠EOD=∠COD= ,再求得∠AOE= ;根 据等腰三角形的性质和 定理来求∠AEO的度数. 𝑩 𝑪 = 𝑪 𝑫 = 𝑫 𝑬 B

核心重难探究 【方法归纳】 解决这类问题既要利用弧与圆心角的关系,又要利用等腰三 角形的性质和三角形的内角和定理,解决圆的有关问题要注 意半径相等这个隐含条件的灵活运用. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题既要利用弧与圆心角的关系,又要利用等腰三 角形的性质和三角形的内角和定理,解决圆的有关问题要注 意半径相等这个隐含条件的灵活运用