
家庭们亚 5三角函数的应用 第3课时 坡度、坡角
5 三角函数的应用 第3课时 坡度、坡角

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.小明同学爱好登山运动,一天他沿坡角为60°的斜坡登山, 此山的坡度是(D) A.1:2 B.2:1 C.1:3 D.V3:1 2.如图,一个人从山脚下的点A出发,沿山坡小路AB走到山顶 点B.已知坡角为20°,山高BC=2千米用科学计算器计算小路 AB的长度,下列按键顺序正确的是(A), B A.2÷sin20= B.2X sin20= 2 C.2÷c0s20= D.2 X tan20= A120 导航页
导航页 基础自主梳理 1.小明同学爱好登山运动,一天他沿坡角为60°的斜坡登山, 此山的坡度是( ). A.1∶2 B.2∶1 C.1∶ 𝟑 D. 𝟑∶1 2.如图,一个人从山脚下的点A出发,沿山坡小路AB走到山顶 点B.已知坡角为20° ,山高BC=2千米.用科学计算器计算小路 AB的长度,下列按键顺序正确的是( ). A.2÷sin20= B.2×sin20= C.2÷cos20= D.2×tan20= D A
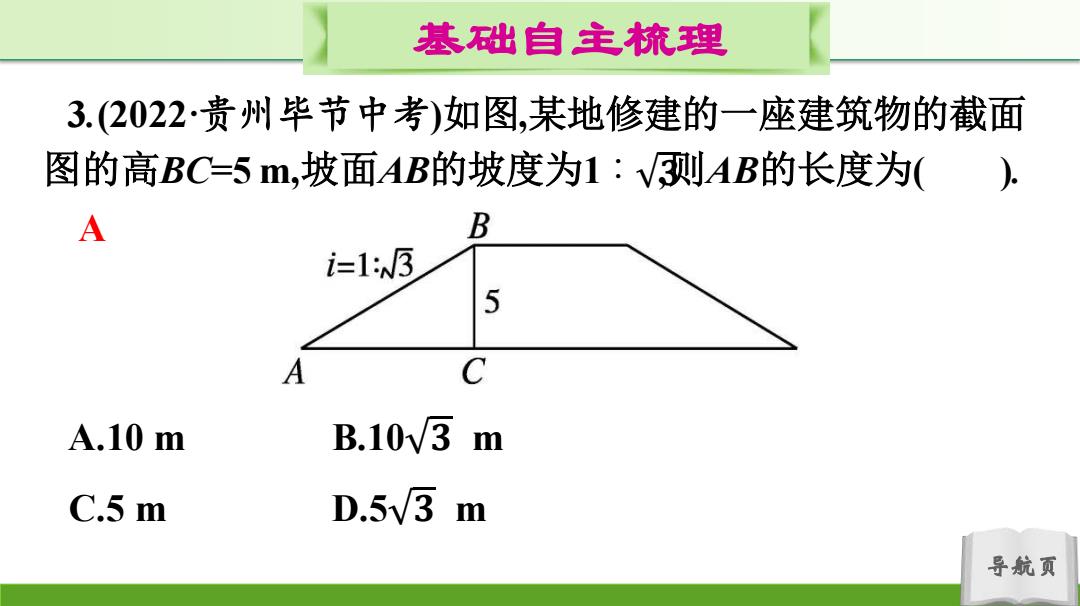
基础自主梳理 3.(2022·贵州毕节中考)如图,某地修建的一座建筑物的截面 图的高BC=5m,坡面AB的坡度为1:V则AB的长度为(), A B i1:w5 5 A C A.10m B.10√3m C.5 m D.5V3 m 导航页
导航页 基础自主梳理 3.(2022·贵州毕节中考)如图,某地修建的一座建筑物的截面 图的高BC=5 m,坡面AB的坡度为1∶ , 𝟑 则AB的长度为( ). A.10 m B.10 𝟑 m C.5 m D.5 𝟑 m A
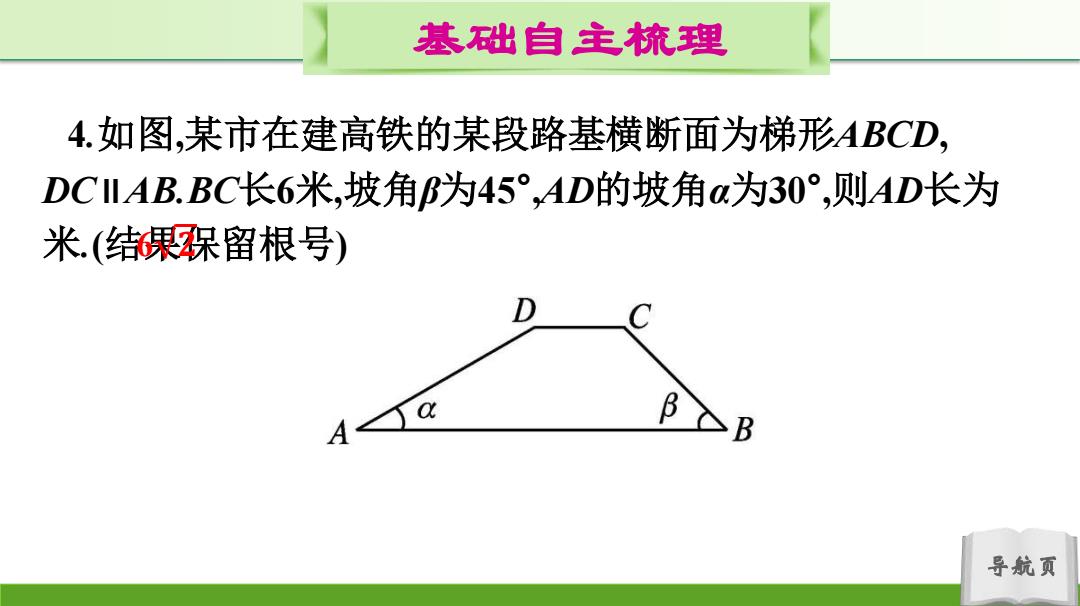
基础自主梳理 4.如图,某市在建高铁的某段路基横断面为梯形ABCD, DCIAB.BC长6米,坡角为45°,AD的坡角a为30°,则AD长为 米.(结乐留根号) D B B 导航页
导航页 基础自主梳理 4.如图,某市在建高铁的某段路基横断面为梯形ABCD, DC∥AB.BC长6米,坡角β为45° ,AD的坡角α为30° ,则AD长为 米.(结果保留根号 6 𝟐 )
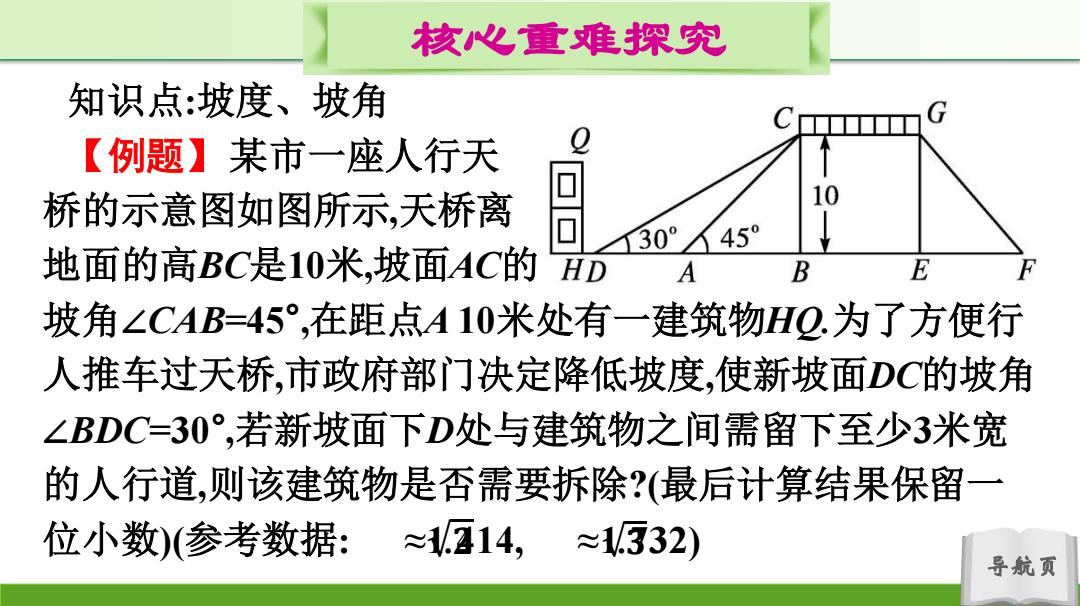
核心重难探究 知识点:坡度、坡角 【例题】某市一座人行天 桥的示意图如图所示,天桥离 10 30° 45 地面的高BC是10米,坡面AC的HD A B E 坡角∠CAB=45°,在距点A10米处有一建筑物HQ.为了方便行 人推车过天桥,市政府部门决定降低坡度,使新坡面DC的坡角 ∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽 的人行道,则该建筑物是否需要拆除?(最后计算结果保留一 位小数)(参考数据:≈114, ≈1532) 导航页
导航页 核心重难探究 知识点:坡度、坡角 【例题】某市一座人行天 桥的示意图如图所示,天桥离 地面的高BC是10米,坡面AC的 坡角∠CAB=45° ,在距点A 10米处有一建筑物HQ.为了方便行 人推车过天桥,市政府部门决定降低坡度,使新坡面DC的坡角 ∠BDC=30° ,若新坡面下D处与建筑物之间需留下至少3米宽 的人行道,则该建筑物是否需要拆除?(最后计算结果保留一 位小数)(参考数据: ≈1 .𝟐414, ≈1 .𝟑732)

核心重难探究 思路点拨:在Rt△ABC,Rt△DBC中,利用锐角三角函数分别 计算 和 ,然后计算 的长,根 据DH与3米人行道的关系求解即可. 导航页
导航页 核心重难探究 思路点拨:在Rt△ABC,Rt△DBC中,利用锐角三角函数分别 计算 和 ,然后计算 的长,根 据DH与3米人行道的关系求解即可

核心重难探究 解:由题意,知AH=10米,BC=10米. 在Rt△ABC中,.'∠CAB=45°, ,∴AB=BC=10米 在Rt△DBC中,.∠CDB=30°, DBan2CDB10W3(米 BC .'DH=AH-(DB-AB)=10-10V3+10=20-10V3≈2.7(米),2.7<3, ,。该建筑物需要拆除 导航页
导航页 核心重难探究 解:由题意,知AH=10米,BC=10米. 在Rt△ABC中,∵∠CAB=45° , ∴AB=BC=10米. 在Rt△DBC中,∵∠CDB=30° , ∴DB= 𝑩𝑪 𝐭𝐚𝐧∠𝑪𝑫𝑩 =10 𝟑(米). ∵DH=AH-(DB-AB)=10-10 𝟑+10=20-10 𝟑≈2.7(米),2.7<3, ∴该建筑物需要拆除

核心重难探究 【方法归纳】 作“两高”构造出直角三角形和矩形,是解有关梯形问题时的 一般思路;当两个直角三角形有公共边时,先求出这条公共边 是解答此类题的一般思路. 导航页
导航页 核心重难探究 【方法归纳】 作“两高”构造出直角三角形和矩形,是解有关梯形问题时的 一般思路;当两个直角三角形有公共边时,先求出这条公共边 是解答此类题的一般思路

新知训练巩固 1.已知某斜坡的坡角为a,坡度=3:4,则sina的值为(B), 4 B 3 D 4-5 2.如图,一辆小车沿坡角为a的斜坡向上行驶了13米,已知cosa 12 ,则小车上升的高度是(A人 A.5米 B.6米 C.6.5米 D.12米 Ja 导航页
导航页 新知训练巩固 1.已知某斜坡的坡角为α,坡度i=3∶4,则sin α的值为( ). A. 𝟑 𝟒 B. 𝟑 𝟓 C. 𝟒 𝟑 D. 𝟒 𝟓 2.如图,一辆小车沿坡角为α的斜坡向上行驶了13米,已知cos α = ,则小车上升的高度是( ). A.5米 B.6米 C.6.5米 D.12米 𝟏𝟐 𝟏𝟑 B A