
家庭们亚 1 锐角三角丞数 第2课时, 正弦和余弦
1 锐角三角函数 第2课时 正弦和余弦

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
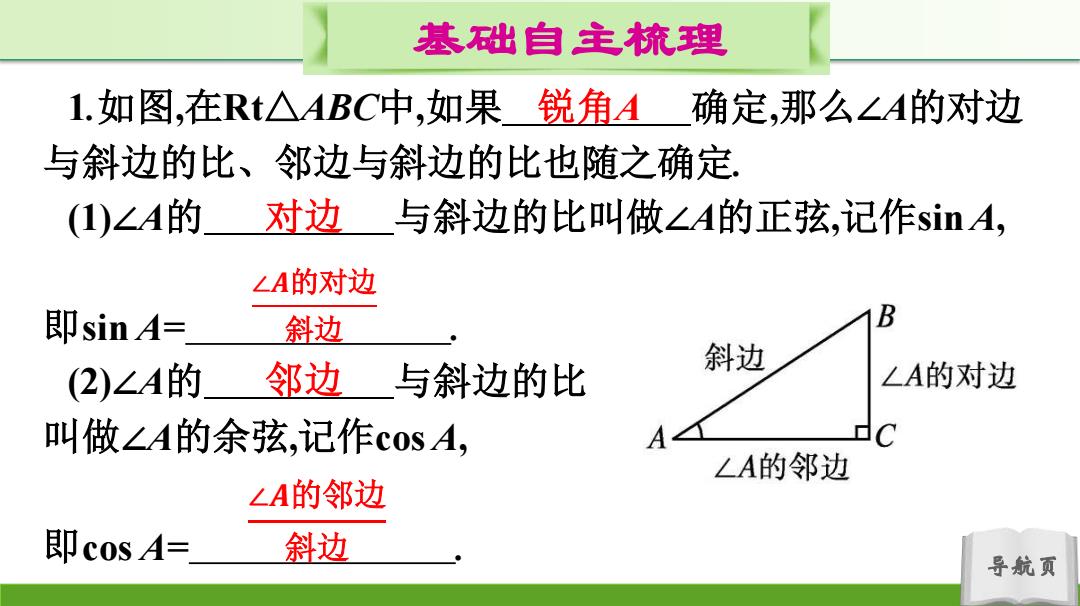
基础自主梳理 1.如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边 与斜边的比、邻边与斜边的比也随之确定 (1)∠A的 对边与斜边的比叫做∠A的正弦,记作sinA, LA的对边 即sinA= 斜边 (2)∠A的 邻边与斜边的比 斜边 ∠A的对边 叫做∠A的余弦,记作cosA, A ∠A的邻边 ∠A的邻边 即c0sA= 斜边 导航页
导航页 基础自主梳理 1.如图,在Rt△ABC中,如果 确定,那么∠A的对边 与斜边的比、邻边与斜边的比也随之确定. (1)∠A的 与斜边的比叫做∠A的正弦,记作sin A, 即sin A= . (2)∠A的 与斜边的比 叫做∠A的余弦,记作cos A, 即cos A= . 锐角A 对边 ∠𝑨的对边 斜边 邻边 ∠𝑨的邻边 斜边
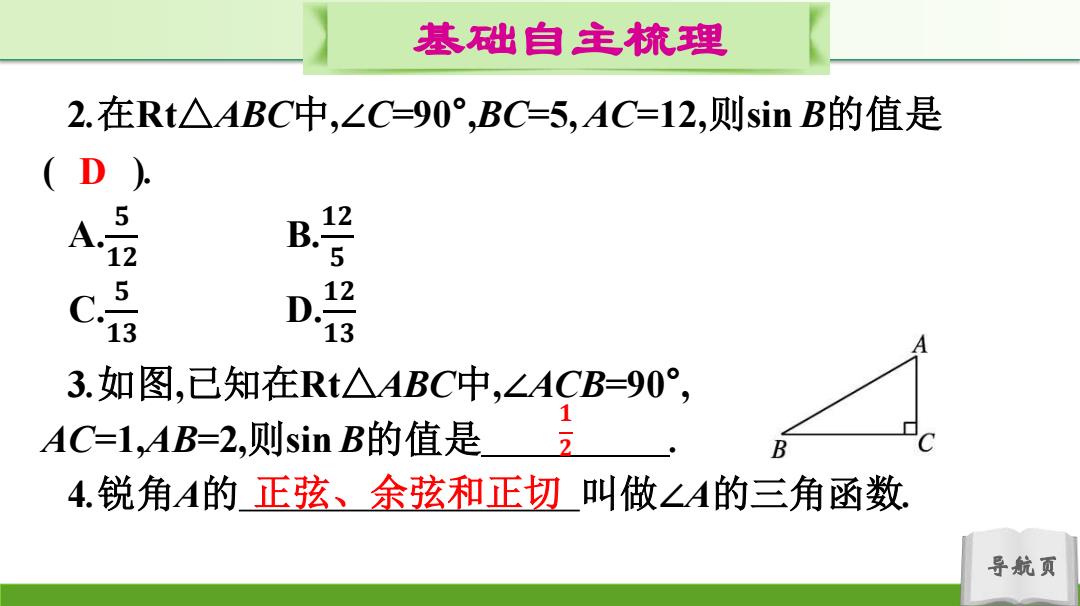
基础自主梳理 2.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是 (D). 5 B. 12 5 D 12 13 13 3.如图,己知在Rt△ABC中,∠ACB=90°, AC=1,AB=2,则sinB的值是 2 B 4.锐角A的正弦、余弦和正切叫做∠A的三角函数 导航页
导航页 基础自主梳理 2.在Rt△ABC中,∠C=90° ,BC=5, AC=12,则sin B的值是 ( ). A. 𝟓 𝟏𝟐 B. 𝟏𝟐 𝟓 C. 𝟓 𝟏𝟑 D. 𝟏𝟐 𝟏𝟑 3.如图,已知在Rt△ABC中,∠ACB=90° , AC=1,AB=2,则sin B的值是 . 4.锐角A的 叫做∠A的三角函数. D 𝟏 𝟐 正弦、余弦和正切

基础自主梳理 温馨提示 1.在锐角三角函数中,自变量∠A的取值范围是0°0. 2.锐角三角函数之间的关系: (1)互余两角的三角函数关系:如果∠A+∠B=90°,那么sin A=cos B,cos A=sin B,tan Atan B=1. (②)同角三角函数关系:sin2A+cos2A=1;tanA=sin叫 cosA' 导航页
导航页 基础自主梳理 温馨提示 1.在锐角三角函数中,自变量∠A的取值范围是0°0. 2.锐角三角函数之间的关系: (1)互余两角的三角函数关系:如果∠A+∠B=90° ,那么sin A=cos B,cos A=sin B,tan A·tan B=1. (2)同角三角函数关系:sin2 A+cos2 A=1;tan A=𝐬𝐢𝐧𝑨 𝐜𝐨𝐬𝑨

基础自主梳理 5.在△ABC中,∠C-=90°,sinA=,3C=4,则AB的值 是 10 6.sinA的值越大,梯子越陡;cosA的值越 小 梯子越陡 导航页
导航页 基础自主梳理 5.在△ABC中,∠C=90°,sin A= ,BC=4,则AB的值 是 . 6.sin A的值越 ,梯子越陡;cos A的值越 , 梯子越陡. 𝟐 𝟓 10 大 小
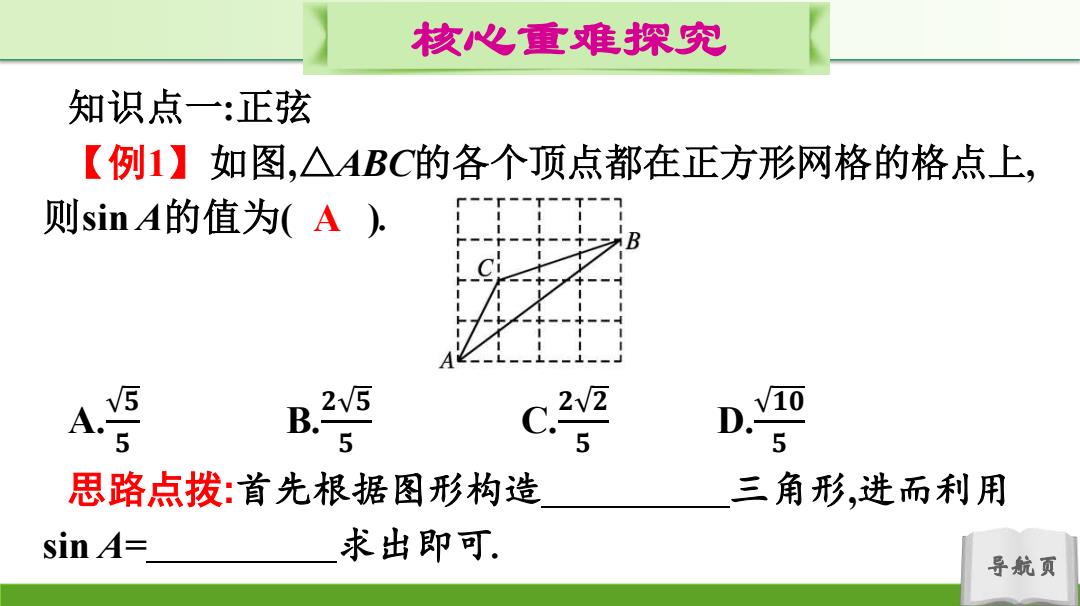
核心重难探究 知识点一:正弦 【例1】如图,△ABC的各个顶点都在正方形网格的格点上, 则sinA的值为(A) 5 B 2V5 C 2√2 D. V10 A. 5 5 5 思路点拨:首先根据图形构造 三角形,进而利用 sin A= 求出即可. 导航页
导航页 核心重难探究 知识点一:正弦 【例1】如图,△ABC的各个顶点都在正方形网格的格点上, 则sin A的值为( ). A. 𝟓 𝟓 B. 𝟐 𝟓 𝟓 C. 𝟐 𝟐 𝟓 D. 𝟏𝟎 𝟓 思路点拨:首先根据图形构造 三角形,进而利用 sin A= 求出即可. A

核心重难探究 【方法归纳】 首先要观察这个角是否在一个直角三角形中,边的比值可否 求出.若不在一个直角三角形中,则可以根据图形的特征构造 成在各边长容易求出的直角三角形中,进而求出这个角的正 弦值. 导航页
导航页 核心重难探究 【方法归纳】 首先要观察这个角是否在一个直角三角形中,边的比值可否 求出.若不在一个直角三角形中,则可以根据图形的特征构造 成在各边长容易求出的直角三角形中,进而求出这个角的正 弦值

核心重难探究 知识点二:余弦 【例2】 在Rt△ABC中,∠C-90°,BC-4,cosA=,AB的长 度是( 0. A.3 B.4 C.5 3 思路点拨: B 如图,根据题意画出图形,可得 5, 设AC=3x>0),则AB=5x,利用勾股定理, 得 ,解出x的值,进而可得AB的长, A 导航页
导航页 核心重难探究 知识点二:余弦 【例2】在Rt△ABC中,∠C=90° ,BC=4,cos A= ,则AB的长 度是( ). 𝟑 𝟓 A.3 B.4 C.5 D. 𝟐𝟎 𝟑 思路点拨: 如图,根据题意画出图形,可得 = , 设AC=3x(x>0),则AB=5x,利用勾股定理, 得 ,解出x的值,进而可得AB的长. 𝟑 𝟓 C

核心重难探究 【方法归纳】 解决这类问题可以根据题意画出图形,直观地找出各个量之 间的关系,利用勾股定理和三角函数求解即可. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题可以根据题意画出图形,直观地找出各个量之 间的关系,利用勾股定理和三角函数求解即可