
家庭们亚 2 二次函数的图象与性质 第1课时 二次函数y=Ax的图象与性质
2 二次函数的图象与性质 第1课时 二次函数y=ax2的图象与性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.二次函数y=x2的图象是一条抛物线,它的开 1向上,且关于 轴对称.对称轴与抛物线的 交点是抛物线的顶点,它是图象的最低点.当x= 0 时,y的值最小,最小值是0 ;当x0时,y随x的增大而增大 导航页
导航页 基础自主梳理 1.二次函数y=x2的图象是一条 ,它的开 口 ,且关于 轴对称.对称轴与抛物线的 交点是抛物线的 ,它是图象的最低点.当x= 时,y的值最小,最小值是 ;当x0时,y随x的增大而 . 抛物线 向上 y 顶点 0 0 减小 增大

基础自主梳理 2.二次函数y=-x2的图象是一条抛物线,它的开口向下 关于 轴对称,对称轴与抛物线的交点是抛物线 的顶点,它是图象的最高点.当=0 时y的值 最大,最大值是0 ;当x0时y随x的增大而 减小 导航页
导航页 基础自主梳理 2.二次函数y=-x 2的图象是一条抛物线,它的开口 , 关于 轴对称,对称轴与抛物线的交点是抛物线 的 ,它是图象的最高点.当x= 时,y的值 最大,最大值是 ;当x0时,y随x的增大而 . 向下 y 顶点 0 0 增大 减小
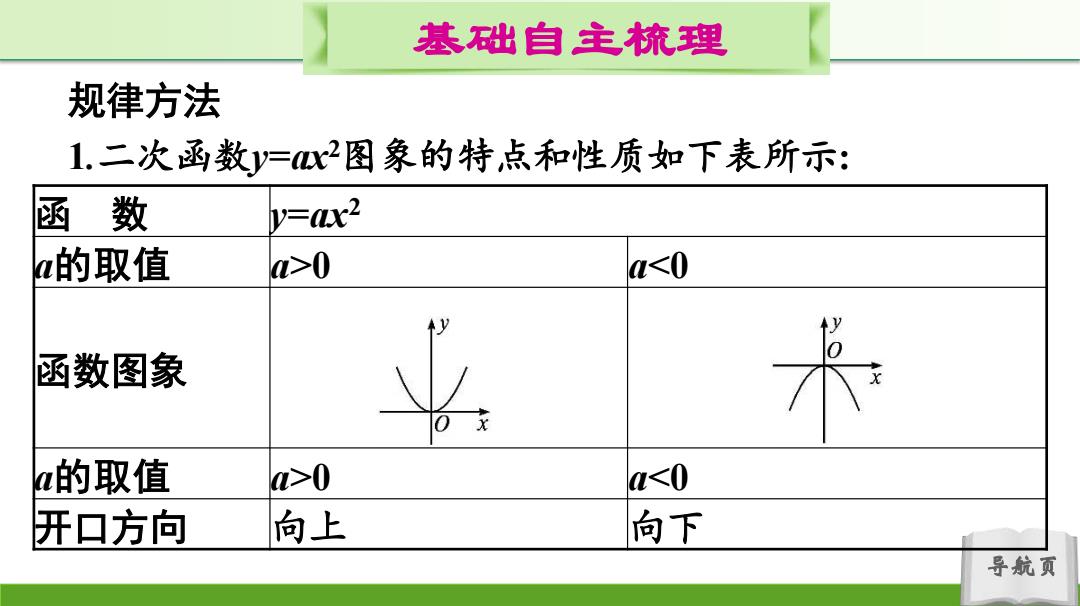
基础自主梳理 规律方法 1.二次函数y=x图象的特,点和性质如下表所示: 函数 y=ax2 a的取值 >0 a0 <0 开口方向 向上 向下 导航页
导航页 基础自主梳理 规律方法 1.二次函数y=ax2图象的特点和性质如下表所示: 函 数 y=ax2 a的取值 a>0 a0 a<0 开口方向 向上 向下

基础自主梳理 对称轴 y轴 顶点坐标 0,0) 当x=0时,函数有最小 当x=0时,函数有最大值 函数最值 值为0 为0 当x0时y随x的增大 当x>0时y随x的增大而 而增大 减小 导航页
导航页 基础自主梳理 对称轴 y轴 顶点坐标 (0,0) 函数最值 当x=0时,函数有最小 值为0 当x=0时,函数有最大值 为0 函数增减性 当x0时,y随x的增大 而增大 当x0时,y随x的增大而 减小

基础自主梳理 2.二次函数y=x2的图象的开口方向由a的符号确定,开口大 小由确定.越大,抛物线开口越小;越小,抛物线开口越大 3.二次函数y=x的性质简记为:抛物线开口向上,左减右增, 最小值为0;抛物线开口向下,左增右减,最大值为0. 4.一般地,抛物线开口向上时没有最大值,抛物线开口向下时 没有最小值 导航页
导航页 基础自主梳理 2.二次函数y=ax2的图象的开口方向由a的符号确定,开口大 小由|a|确定.|a|越大,抛物线开口越小;|a|越小,抛物线开口越大. 3.二次函数y=ax2的性质简记为:抛物线开口向上,左减右增, 最小值为0;抛物线开口向下,左增右减,最大值为0. 4.一般地,抛物线开口向上时没有最大值,抛物线开口向下时 没有最小值

基础自主梳理 3.二次函数y=x2的图象开口方向是向上(填“向上” 或“向下”) 导航页
导航页 基础自主梳理 3.二次函数y=x2的图象开口方向是 .(填 “向上” 或“向下”) 向上

核心重难探究 知识点一:二次函数y=x2的图象与性质 【例1】在同一坐标系中,二次函数y=3x2y=x2y-x2的图 象的共同特点是(D A.关于y轴对称,开口向上 B.关于y轴对称,y随x的增大而增大 C.关于y轴对称y随x的增大而减小 D关于y轴对称,顶点是原点 思路点拨:二次函数y=2的图象的对称轴、顶点坐标与a的 取值有什么关系?开口方向、增减性和最值呢? 导航页
导航页 核心重难探究 知识点一:二次函数y=ax2的图象与性质 【例1】在同一坐标系中,二次函数y=3x 2 ,y= x2 ,y=- x 2的图 象的共同特点是( ). A.关于y轴对称,开口向上 B.关于y轴对称,y随x的增大而增大 C.关于y轴对称,y随x的增大而减小 D.关于y轴对称,顶点是原点 思路点拨:二次函数y=ax2的图象的对称轴、顶点坐标与a的 取值有什么关系?开口方向、增减性和最值呢? 𝟏 𝟑 𝟏 𝟑 D

核心重难探究 【方法归纳】 表达式形如y=x的抛物线的共同特点:关于y轴对称,顶点是 原点,的正负决定开口方向 导航页
导航页 核心重难探究 【方法归纳】 表达式形如y=ax2的抛物线的共同特点:关于y轴对称,顶点是 原点,a的正负决定开口方向