
家庭像四 4圆周角和圆心角的关系 第2课时 圆内接四边形
4 圆周角和圆心角的关系 第2课时 圆内接四边形

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.直径所对的圆周角是直角; 90°的圆周角所 对的弦是直径 温馨提示 1.当圆中有直径时,通常作出直径所对的0°的圆周角,即“见 直径出直角” 2.当圆中有90°的圆周角而没有直径时,通常作出0°的圆周 角所对的直径,即“见直角出直径”. 导航页
导航页 基础自主梳理 1.直径所对的圆周角是 ; 的圆周角所 对的弦是直径. 温馨提示 1.当圆中有直径时,通常作出直径所对的90°的圆周角,即“见 直径出直角” . 2.当圆中有90°的圆周角而没有直径时,通常作出90°的圆周 角所对的直径,即“见直角出直径” . 直角 90°

基础自主梳理 2.如图,AB是⊙O的直径,点C是⊙O上一点, B 连接AC,BC,则∠C的度数是(B). A.60° B.90° C.120° D.150° 3.如果一个四边形的所有顶点都在圆上,那么这个四边形叫 做圆内接四边形,这个圆叫做四边形的外接圆 4.圆内接四边形的对角互补 导航页
导航页 基础自主梳理 2.如图,AB是☉O的直径,点C是☉O上一点, 连接AC,BC,则∠C的度数是( ). A.60° B.90° C.120° D.150° 3.如果一个四边形的所有顶点都在圆上,那么这个四边形叫 做 ,这个圆叫做 . 4.圆内接四边形的对角 . B 圆内接四边形 四边形的外接圆 互补
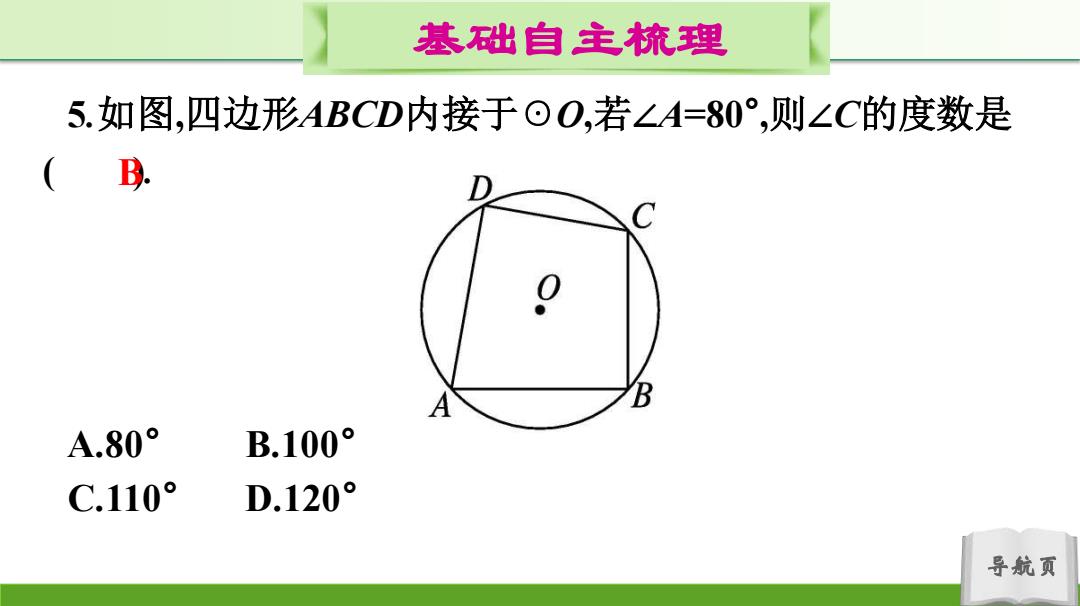
基础自主梳理 5.如图,四边形ABCD内接于⊙O,若∠A=80°,则∠C的度数是 (D. A A.80° B.100° C.110° D.120° 导航页
导航页 基础自主梳理 5.如图,四边形ABCD内接于☉O,若∠A=80° ,则∠C的度数是 ( ). A.80° B.100° C.110° D.120° B
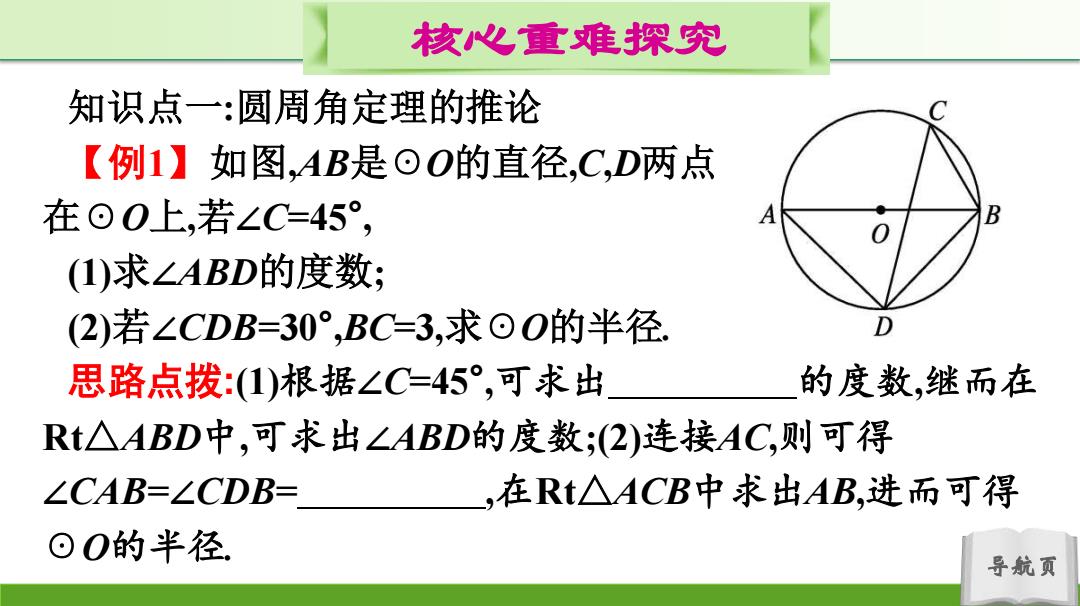
核心重难探究 知识点一:圆周角定理的推论 【例1】如图,AB是⊙O的直径,C,D两点 在⊙0上,若∠C=45°, B (1)求∠ABD的度数; (2)若∠CDB=30°,BC=3,求⊙O的半径 D 思路点拨:(1)根据∠C=45°,可求出 的度数,继而在 Rt△ABD中,可求出∠ABD的度数;2)连接AC,则可得 ∠CAB=∠CDB= ,在Rt△ACB中求出AB,进而可得 ⊙O的半径 导航页
导航页 核心重难探究 知识点一:圆周角定理的推论 【例1】如图,AB是☉O的直径,C,D两点 在☉O上,若∠C=45° , (1)求∠ABD的度数; (2)若∠CDB=30° ,BC=3,求☉O的半径. 思路点拨:(1)根据∠C=45° ,可求出 的度数,继而在 Rt△ABD中,可求出∠ABD的度数;(2)连接AC,则可得 ∠CAB=∠CDB= ,在Rt△ACB中求出AB,进而可得 ☉O的半径
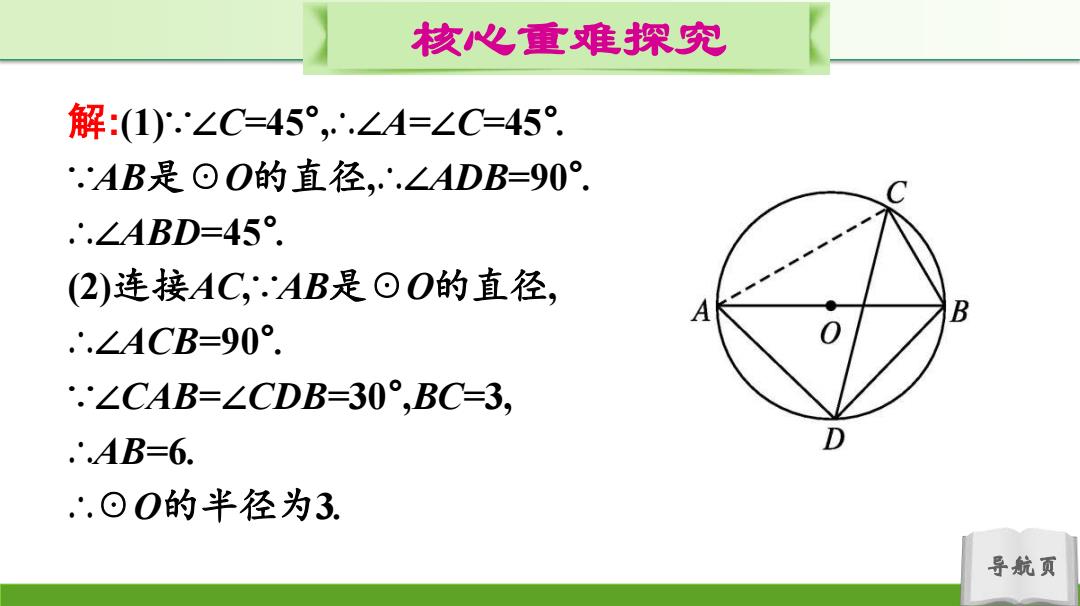
核心重难探究 解:1)∠C=45°,∴∠A=∠C=45°. .AB是回O的直径,∴.∠ADB=90°. ..∠ABD=45°. (2)连接AC,.AB是⊙O的直径, B .∴.∠ACB=90°. .'∠CAB=∠CDB=30°,BC=3, ‘AB=6. D .⊙0的半径为3. 导航页
导航页 核心重难探究 解:(1)∵∠C=45° ,∴∠A=∠C=45° . ∵AB是☉O的直径,∴∠ADB=90° . ∴∠ABD=45° . (2)连接AC,∵AB是☉O的直径, ∴∠ACB=90° . ∵∠CAB=∠CDB=30° ,BC=3, ∴AB=6. ∴☉O的半径为3

核心重难探究 【方法归纳】 在解圆的有关问题时,常常需要添加辅助线,构成直径所对 的圆周角,这种基本技能一定要掌握 导航页
导航页 核心重难探究 【方法归纳】 在解圆的有关问题时,常常需要添加辅助线,构成直径所对 的圆周角,这种基本技能一定要掌握

核心重难探究 知识点二:圆内接四边形的性质 D 【例2】如图,四边形ABCD内接于⊙O,它的 一个外角∠EBC=65°,分别连接AC,BD,若 AC=AD,则∠DBC的度数为(A)片 A.50° B.55° B C.65° D.70° 导航页
导航页 核心重难探究 知识点二:圆内接四边形的性质 【例2】如图,四边形ABCD内接于☉O,它的 一个外角∠EBC=65° ,分别连接AC,BD,若 AC=AD,则∠DBC的度数为( ). A.50° B.55° C.65° D.70° A

核心心重难探究 思路点拨:先根据圆内接四边形的性质得出∠ADC= 再根据AC=AD得出∠ACD=∠ADC= ,故可根据三 角形内角和定理求出∠CAD= ,再由圆周角定理得 出∠DBC=∠CAD= 【方法归纳】 圆内接四边形的性质是沟通角相等关系的重要依据,在应用 此性质时,要注意与圆周角定理结合起来在应用时要注意是 对角互补,而不是邻角. 导航页
导航页 核心重难探究 思路点拨:先根据圆内接四边形的性质得出∠ADC= , 再根据AC=AD得出∠ACD=∠ADC= ,故可根据三 角形内角和定理求出∠CAD= ,再由圆周角定理得 出∠DBC=∠CAD= . 【方法归纳】 圆内接四边形的性质是沟通角相等关系的重要依据,在应用 此性质时,要注意与圆周角定理结合起来.在应用时要注意是 对角互补,而不是邻角