
家庭值亚 3 确定二次函数的表达式 第1课时 已知两点确定二次函数表达式(一般式,顶点式)
3 确定二次函数的表达式 第1课时 已知两点确定二次函数表达式(一般式,顶点式)

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.在利用待定系数法求二次函数关系式时,要根据题目给定 的条件,选择恰当的方法设出关系式,从而代入数值求 解 2.已知抛物线y=2-3x+c经过A(-1,10),B(2,4)两点,则抛物线 的表达式为y=x23x+6 3.若给出抛物线的顶点坐标,通常设顶点式求关系式。一般解 题思路如下: (1)设二次函数的关系式为y=Mx-h)2+k(呋0); 导航页
导航页 基础自主梳理 1.在利用待定系数法求二次函数关系式时,要根据题目给定 的 ,选择恰当的方法设出关系式,从而代入 求 解. 2.已知抛物线y=ax2 -3x+c经过A(-1,10),B(2,4)两点,则抛物线 的表达式为 . 3.若给出抛物线的顶点坐标,通常设顶点式求关系式.一般解 题思路如下: (1)设二次函数的关系式为 ; 条件 数值 y=x2 -3x+6 y=a(x-h) 2+k(a≠0)

基础自主梳理 (2)把顶点的坐标代入所设的关系式中,转化成关于α的 一元一次方程; 3)解方程求得 的值; (4)把 的值代入所设的关系式中,得出二次函数 的关系式 4.经过原点且顶点坐标为(-1,2)的抛物线的表达式 为y=-2c+1)2+2 导航页
导航页 基础自主梳理 (2)把顶点的坐标代入所设的关系式中,转化成关于 的 一元一次方程; (3)解方程求得 的值; (4)把 的值代入所设的关系式中,得出二次函数 的关系式. 4.经过原点且顶点坐标为(-1,2)的抛物线的表达式 为 . a a a y=-2(x+1)2+2

核心重难探究 知识点一:一般式(已知两点) 【例1】下表给出了二次函数y=x2+bx+c的一些对应值: 3 10 (1)根据表格中的数据,确定b,c,n的值; (2)直接写出0≤x≤2时的最大值, 导航页
导航页 核心重难探究 知识点一:一般式(已知两点) 【例1】下表给出了二次函数y=-x 2+bx+c的一些对应值: x … -2 -1 0 1 2 3 … y … 5 n c 2 -3 -10 … (1)根据表格中的数据,确定b,c,n的值; (2)直接写出0≤x≤2时y的最大值

核心重难探究 思路点拨:1)把 分别代入y=-x2+bx+c中得到关于 b,c的方程组,解方程组即可得到b,c的值;然后计算x= 时y的值即可得到n的值;2)利用表中数据求解 导航页
导航页 核心重难探究 思路点拨:(1)把 分别代入y=-x 2+bx+c中得到关于 b,c的方程组,解方程组即可得到b,c的值;然后计算x= 时y的值即可得到n的值;(2)利用表中数据求解

核心重难探究 解:1)根据表格数据可得 -4-2b+c=5,解得 b=-2, -1+b+c=2, c=5. ∴y=-x2-2x+5. 当x=-1时y=-x2-2x+5=6,即n=6. (2)根据表中数据得当0≤x≤2时,y的最大值是5. 【方法归纳】 根据所给的表格求二次函数关系式时,要仔细观察表格中的 数据,选择恰当的数据代入数值求解 导航页
导航页 核心重难探究 解:(1)根据表格数据可得 -𝟒-𝟐𝒃 + 𝒄 = 𝟓, -𝟏 + 𝒃 + 𝒄 = 𝟐, 解得 𝒃 = -𝟐, 𝒄 = 𝟓. ∴y=-x 2 -2x+5. 当x=-1时,y=-x 2 -2x+5=6,即n=6. (2)根据表中数据得当0≤x≤2时,y的最大值是5. 【方法归纳】 根据所给的表格求二次函数关系式时,要仔细观察表格中的 数据,选择恰当的数据代入数值求解
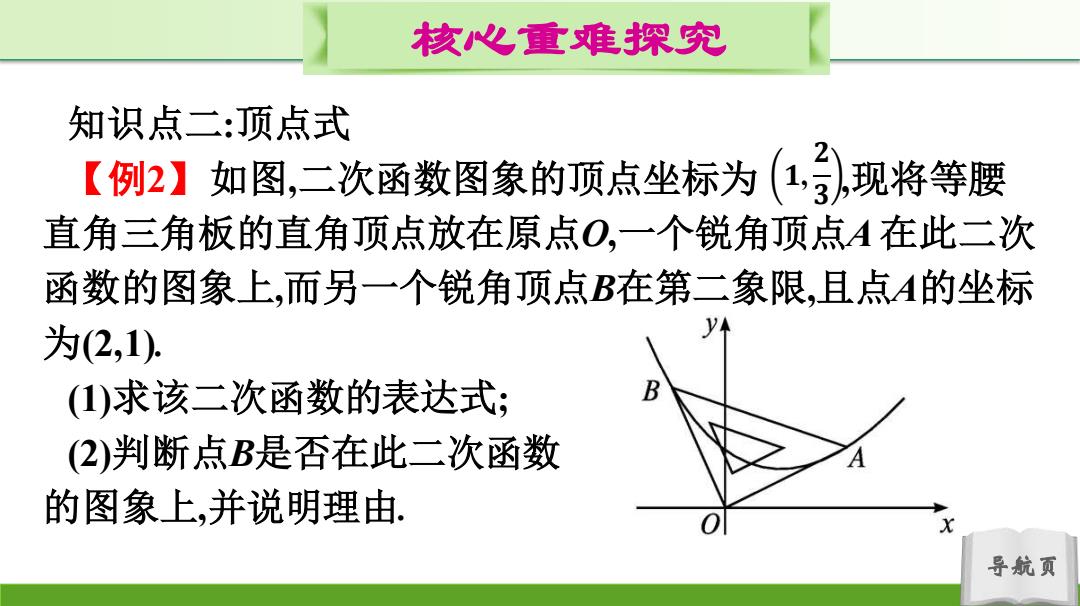
核心重难探究 知识点二:顶点式 【例2】如图,二次函数图象的顶点坐标为(1,现将等腰 直角三角板的直角顶点放在原点O,一个锐角顶点A在此二次 函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标 为(2,1). (1)求该二次函数的表达式; (2)判断点B是否在此二次函数 的图象上,并说明理由. 导航页
导航页 核心重难探究 知识点二:顶点式 【例2】如图,二次函数图象的顶点坐标为 ,现将等腰 直角三角板的直角顶点放在原点O,一个锐角顶点A 在此二次 函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标 为(2,1). (1)求该二次函数的表达式; (2)判断点B是否在此二次函数 的图象上,并说明理由. 𝟏, 𝟐 𝟑

核心重难探究 思路点拨:(1)由二次函数图象的顶点坐标为1),可设函数 表达式为 ,再将A的坐标(2,1)代入,求出的值,即可 得出该二次函数的表达式;2)过点A,B分别作AC⊥x轴,BD⊥x 轴,垂足分别为,点C,D.易证得△AOC坐 ,可得出 DO-AC- BD-OC- ,那么 B( ),再将x= 代入(1)中所 求表达式,即可判断点B在这个函数图象上 导航页
导航页 核心重难探究 思路点拨:(1)由二次函数图象的顶点坐标为 ,可设函数 表达式为 ,再将A的坐标(2,1)代入,求出a的值,即可 得出该二次函数的表达式;(2)过点A,B分别作AC⊥x轴,BD⊥x 轴,垂足分别为点C,D.易证得△AOC≌ ,可得出 DO=AC= ,BD=OC= ,那么 B( , ),再将x= 代入(1)中所 求表达式,即可判断点B在这个函数图象上. 𝟏, 𝟐 𝟑

核心重难探究 解:()设二次函数的表达式为=ac-12+子 ·图象过A(2,1),a+子1,即号 “该二次函数的表达式为心1+号 导航页
导航页 核心重难探究 解:(1)设二次函数的表达式为 y=a(x-1)2 + 𝟐 𝟑 , ∵图象过 A(2,1),∴a+𝟐 𝟑 =1,即 a= 𝟏 𝟑 . ∴该二次函数的表达式为 y= 𝟏 𝟑 (x-1)2 + 𝟐 𝟑