
家庭馆亚 第一章 直角三角形的边确关系 6 利用三角丞数测高
第一章 直角三角形的边角关系 6 利用三角函数测高

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.测量倾斜角 (1)测量倾斜角可以用测倾器 .简单的测倾器 由度盘 铅锤 和 支杆 组成(如图). (2)使用测倾器测量倾斜角的步骤如下: ①把支杆竖直插入地面,使支杆的中心线、 铅垂线和度盘的 0° 刻度线重合,这时 度盘的顶线PO在水平 位置 ②转动度盘,使度盘的直径对准目标M,记下此时铅垂线所 指的度数即可. 导航页
导航页 基础自主梳理 1.测量倾斜角 (1)测量倾斜角可以用 .简单的测倾器 由 、 和 组成(如图). (2)使用测倾器测量倾斜角的步骤如下: ①把支杆竖直插入地面,使支杆的中心线、 铅垂线和度盘的 刻度线重合,这时 度盘的顶线PQ在 位置. ②转动度盘,使度盘的直径对准目标M,记下此时铅垂线所 指的度数即可. 测倾器 度盘 铅锤 支杆 0° 水平

基础自主梳理 2.测量底部可以到达的物体的高度 (1)所谓“底部可以到达”,就是在地面上可以 无障碍地直接测得 测点与被测物体的 底部之间的距离 (2)如图,要测量物体MN的高度,可按下列步骤进行: ①在测点A处安置测倾器,测得M的仰角∠MCE =0 ②量出测点A到物体底部N的水平距离 AN =l. ③量出测倾器的高度 AC =. 根据以上测量数据,便能求出物体MN的高度为+Itan a。 航页
导航页 基础自主梳理 2.测量底部可以到达的物体的高度 (1)所谓“底部可以到达”,就是在地面上可以 无障碍地直接测得 与被测物体的 底部之间的距离. (2)如图,要测量物体MN的高度,可按下列步骤进行: ①在测点A处安置测倾器,测得M的仰角 =α. ②量出测点A到物体底部N的水平距离 =l. ③量出测倾器的高度 =a. 根据以上测量数据,便能求出物体MN的高度为 . 测点 ∠MCE AN AC a+ltan α
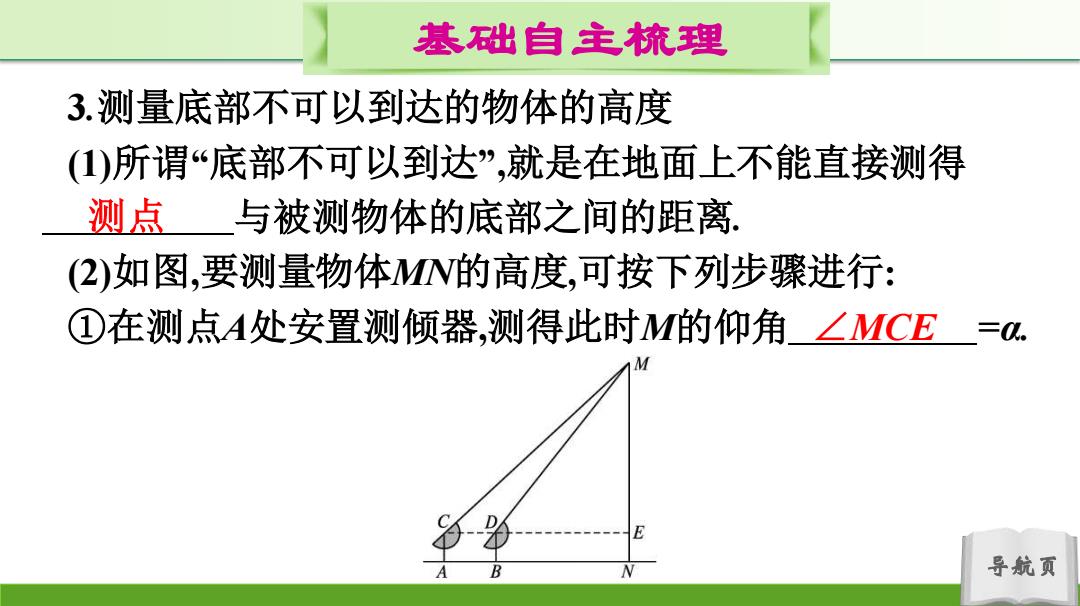
基础自主梳理 3.测量底部不可以到达的物体的高度 ()所谓“底部不可以到达”,就是在地面上不能直接测得 测点与被测物体的底部之间的距离. (2)如图,要测量物体MN的高度,可按下列步骤进行: ①在测点A处安置测倾器,测得此时M的仰角∠MCE =0 导航页
导航页 基础自主梳理 3.测量底部不可以到达的物体的高度 (1)所谓“底部不可以到达”,就是在地面上不能直接测得 与被测物体的底部之间的距离. (2)如图,要测量物体MN的高度,可按下列步骤进行: ①在测点A处安置测倾器,测得此时M的仰角 =α. 测点 ∠MCE

基础自主梳理 ②在测点A与物体之间的B处安置测倾器(A,B与N在一条直 线上,且A,B之间的距离可以直接测得),测得此时M的仰角 ∠MDE=B. ③量出测倾器的高度AC BD =,以及测点 A,B之间的距离AB =b. btana.tanβ 根据以上测量数据,便能求出物体MN的高度为叶 tanβ-tana。 导航页
导航页 基础自主梳理 ②在测点A与物体之间的B处安置测倾器(A,B与N在一条直 线上,且A,B之间的距离可以直接测得),测得此时M的仰角 =β. ③量出测倾器的高度 = =a,以及测点 A,B之间的距离 =b. 根据以上测量数据,便能求出物体MN的高度为 . ∠MDE AC BD AB a+𝒃𝐭𝐚𝐧𝜶·𝐭𝐚𝐧𝜷 𝐭𝐚𝐧𝜷-𝐭𝐚𝐧𝜶
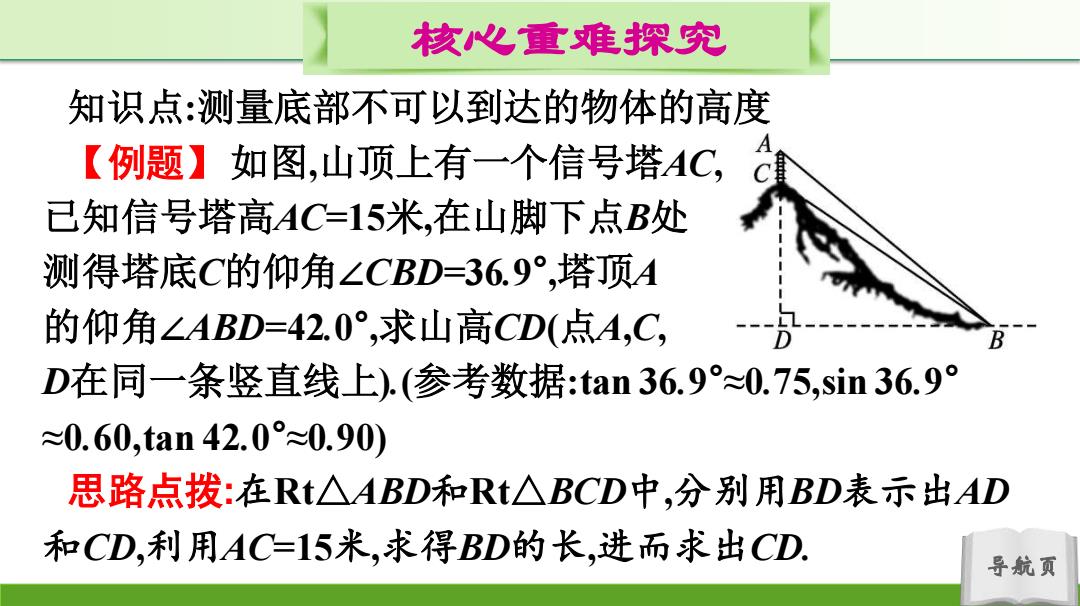
核心重难探究 知识点:测量底部不可以到达的物体的高度 【例题】如图,山顶上有一个信号塔AC, 已知信号塔高AC=15米,在山脚下点B处 测得塔底C的仰角∠CBD=36.9°,塔顶A 的仰角∠ABD=42.0°,求山高CD(点A,C, D在同一条竖直线上).(参考数据:tan36.9°≈0.75,sin36.9° ≈0.60,tan42.0°≈0.90) 思路点拨:在Rt△ABD和Rt△BCD中,分别用BD表示出AD 和CD,利用AC=15米,求得BD的长,进而求出CD 导航页
导航页 核心重难探究 知识点:测量底部不可以到达的物体的高度 【例题】 如图,山顶上有一个信号塔AC, 已知信号塔高AC=15米,在山脚下点B处 测得塔底C的仰角∠CBD=36.9° ,塔顶A 的仰角∠ABD=42.0° ,求山高CD(点A,C, D在同一条竖直线上).(参考数据:tan 36.9°≈0.75,sin 36.9° ≈0.60,tan 42.0°≈0.90) 思路点拨:在Rt△ABD和Rt△BCD中,分别用BD表示出AD 和CD,利用AC=15米,求得BD的长,进而求出CD

核心重难探究 解:由题意,在Rta4BD中,an∠ABD品 tan420°00.9,AD-09BD, 在RIARCD中,n∠CBD品 .tan36.9°=cD0.75,CD0.75BD. BD .AC=AD-CD,.∴.15=0.15BD, ∴.BD=100(米),∴.CD=0.75BD=75(米) 答:山高CD约为75米. 导航页
导航页 核心重难探究 ∵AC=AD-CD,∴15=0.15BD, ∴BD=100(米),∴CD=0.75BD=75(米). 答:山高CD约为75米. 解:由题意,在 Rt△ABD 中,tan∠ABD=𝑨𝑫 𝑩𝑫 , ∴tan 42.0°= 𝑨𝑫 𝑩𝑫 ≈0.9,∴AD≈0.9BD. 在 Rt△BCD 中,tan∠CBD=𝑪𝑫 𝑩𝑫 , ∴tan 36.9°= 𝑪𝑫 𝑩𝑫 ≈0.75,∴CD≈0.75BD

核心重难探究 【方法归纳】 解决这类问题首先要找到相关联的直角三角形,当图形中没 有直角三角形时,要通过作高或垂线构造直角三角形,正确利 用锐角三角函数求解即可. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题首先要找到相关联的直角三角形,当图形中没 有直角三角形时,要通过作高或垂线构造直角三角形,正确利 用锐角三角函数求解即可
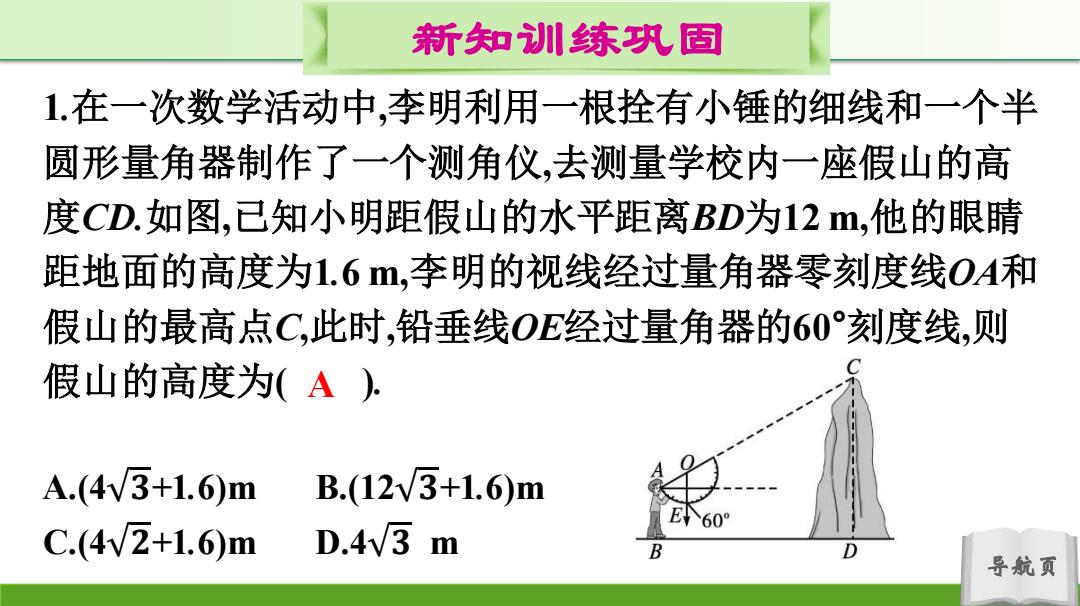
新知训练巩固 1.在一次数学活动中,李明利用一根拴有小锤的细线和一个半 圆形量角器制作了一个测角仪,去测量学校内一座假山的高 度CD.如图,已知小明距假山的水平距离BD为12m,他的眼睛 距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和 假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则 假山的高度为(A) A.(4V3+1.6)m B.(123+1.6)m 60° C.(4v2+1.6)m D.4V3 m 导航页
导航页 新知训练巩固 1.在一次数学活动中,李明利用一根拴有小锤的细线和一个半 圆形量角器制作了一个测角仪,去测量学校内一座假山的高 度CD.如图,已知小明距假山的水平距离BD为12 m,他的眼睛 距地面的高度为1.6 m,李明的视线经过量角器零刻度线OA和 假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则 假山的高度为( ). A.(4 𝟑+1.6)m B.(12 𝟑+1.6)m C.(4 𝟐+1.6)m D.4 𝟑 m A