
家庭馆亚 4圆周角和圆心角的关系 第l课时 圆周角和圆心角的关系
4 圆周角和圆心角的关系 第1课时 圆周角和圆心角的关系

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.顶点在 圆上,两边分别与圆还有另一个交点的角叫 圆周角. 2.圆周角的度数等于它所对弧上的圆心角度数的一 半 3同孤或等 、所对的圆周角相等 导航页
导航页 基础自主梳理 1.顶点在 ,两边分别与圆还有另一个交点的角叫 圆周角. 2.圆周角的度数等于它所对弧上的 度数的一 半. 3.同弧或 所对的圆周角相等. 圆上 圆心角 等弧

基础自主梳理 温馨提示 1.圆周角与圆心角的区别:圆周角的顶点在圆上,圆心角的顶 点是圆心 2.圆周角定理及其推论的适用条件是在同圆或等圆中. 3.同一条孤弧所对的圆周角有无数个,它们都相等 4.在同圆或等圆中,相等的圆周角所对的孤相等. 5.在同圆或等圆中,同一条弦所对的圆周角不一定相等,只有 弦的同侧的圆周角相等. 导航页
导航页 基础自主梳理 温馨提示 1.圆周角与圆心角的区别:圆周角的顶点在圆上,圆心角的顶 点是圆心. 2.圆周角定理及其推论的适用条件是在同圆或等圆中. 3.同一条弧所对的圆周角有无数个,它们都相等. 4.在同圆或等圆中,相等的圆周角所对的弧相等. 5.在同圆或等圆中,同一条弦所对的圆周角不一定相等,只有 弦的同侧的圆周角相等
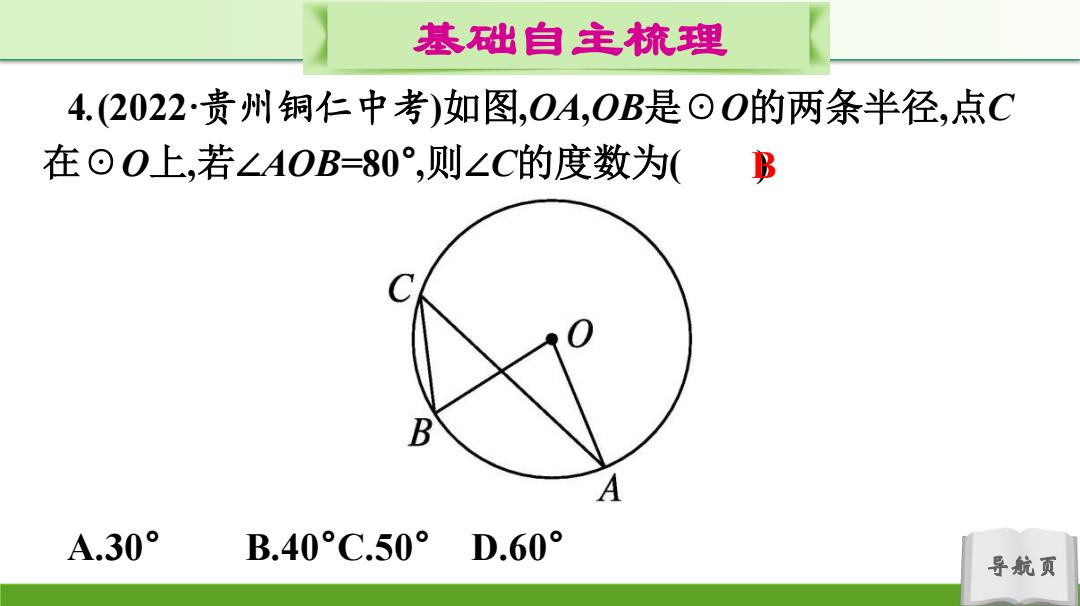
基础自主梳理 4.(2022·贵州铜仁中考)如图,OA,OB是⊙O的两条半径,点C 在⊙O上,若∠AOB=80°,则∠C的度数为( B A A.30° B.40°C.50°D.60° 导航页
导航页 基础自主梳理 4.(2022·贵州铜仁中考)如图,OA,OB是☉O的两条半径,点C 在☉O上,若∠AOB=80° ,则∠C的度数为( ). A.30° B.40°C.50° D.60° B
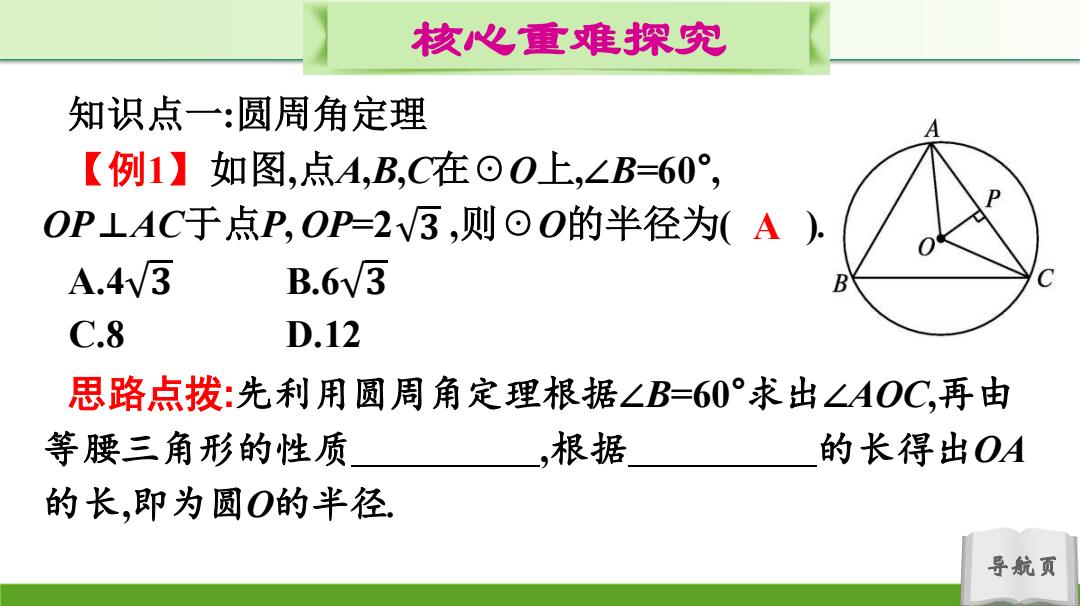
核心重难探究 知识点一:圆周角定理 【例1】如图,点A,B,C在⊙O上,∠B=60°, OP⊥AC于点P,OP=23,则⊙O的半径为A). A.4v3 B.6v3 B C.8 D.12 思路点拨:先利用圆周角定理根据∠B=60°求出∠AOC,再由 等腰三角形的性质 ,根据 的长得出OA 的长,即为圆O的半径 导航页
导航页 核心重难探究 知识点一:圆周角定理 【例1】如图,点A,B,C在☉O上,∠B=60° , OP⊥AC于点P, OP=2 ,则☉O的半径为( ). A.4 𝟑 B.6 𝟑 C.8 D.12 𝟑 思路点拨:先利用圆周角定理根据∠B=60°求出∠AOC,再由 等腰三角形的性质 ,根据 的长得出OA 的长,即为圆O的半径. A

核心重难探究 【方法归纳】 利用圆周角定理,知道圆周角的度数可求同弧所对圆心角的 度数:知道圆心角的度数可求同弧所对圆周角的度数 导航页
导航页 核心重难探究 【方法归纳】 利用圆周角定理,知道圆周角的度数可求同弧所对圆心角的 度数;知道圆心角的度数可求同弧所对圆周角的度数
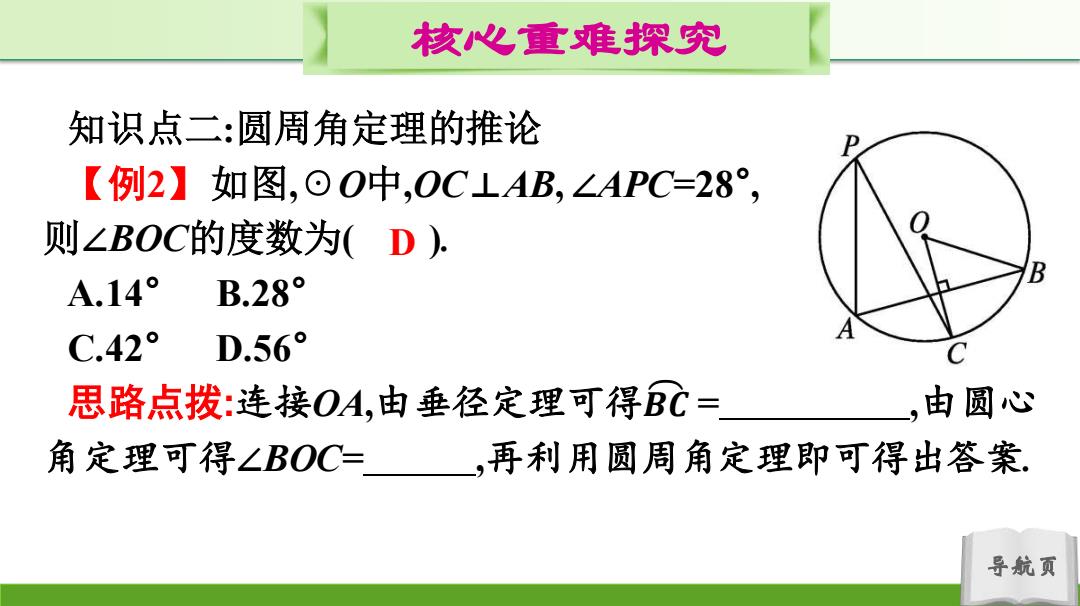
核心重难探究 知识点二:圆周角定理的推论 【例2】如图,⊙O中,OCLAB,∠APC=28°, 则∠BOC的度数为(D). B A.14° B.28° C.42° D.56° 思路点拨:连接OA,由垂径定理可得BC= ,由圆心 角定理可得∠BOC=,再利用圆周角定理即可得出答案. 导航页
导航页 核心重难探究 知识点二:圆周角定理的推论 【例2】如图,☉O中,OC⊥AB, ∠APC=28° , 则∠BOC的度数为( ). A.14° B.28° C.42° D.56° 思路点拨:连接OA,由垂径定理可得 = ,由圆心 角定理可得∠BOC= ,再利用圆周角定理即可得出答案. 𝑩 𝑪 D

核心重难探究 【方法归纳】 圆周角和圆心角的转化可通过作圆的半径构造等腰三角形 导航页
导航页 核心重难探究 【方法归纳】 圆周角和圆心角的转化可通过作圆的半径构造等腰三角形

新知训练巩固 1.如图所示,图中的∠AOB是圆周角的是(B). A B A B A A B A. B. D 导航页
导航页 新知训练巩固 1.如图所示,图中的∠AOB是圆周角的是( B )