
家庭缠亚 2 二次函数的图象与性质 第5课时 二次函数y=ax2+bx+C的图象与性质
2 二次函数的图象与性质 第5课时 二次函数y=ax2+bx+c的图象与性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
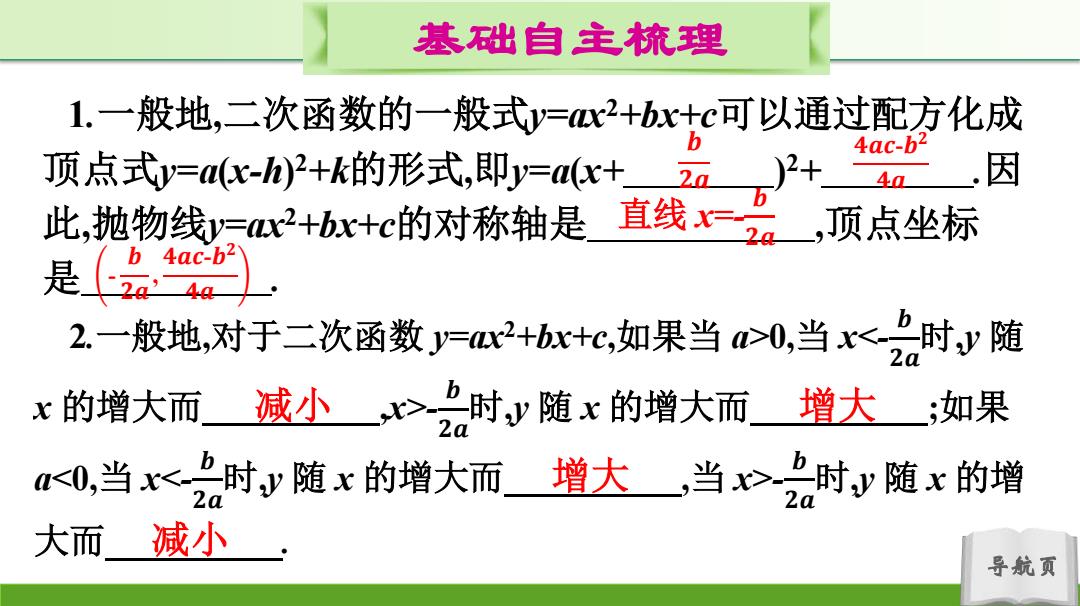
基础自主梳理 1.一般地,二次函数的一般式y=x2+bx+c可以通过配方化成 4ac-b2 顶点式y=c-h)2+k的形式,即y=x+2a)2+ 因 b 此,抛物线y=x2+bx+c的对称轴是 直线。一,顶点坐标 b 4ac-b2 是2a4 2.一般地,对于二次函数=2+bx+c,如果当心0,当x,时y随x的增大而 增大如果 2。 <0,当x<时,y随x的增大而 2a 增大一当x名时y随x的增 大而减小 导航页
导航页 基础自主梳理 1.一般地,二次函数的一般式y=ax2+bx+c可以通过配方化成 顶点式y=a(x-h) 2+k的形式,即y=a(x+ ) 2+ .因 此,抛物线y=ax2+bx+c的对称轴是 ,顶点坐标 是 . 2.一般地,对于二次函数 y=ax2 +bx+c,如果当 a>0,当 x- 𝒃 𝟐𝒂 时,y 随 x 的增大而 ;如果 a- 𝒃 𝟐𝒂 时,y 随 x 的增 大而 . 𝒃 𝟐𝒂 𝟒𝒂𝒄-𝒃 𝟐 𝟒𝒂 直线 x=- 𝒃 𝟐𝒂 - 𝒃 𝟐𝒂 , 𝟒𝒂𝒄-𝒃 𝟐 𝟒𝒂 减小 增大 增大 减小

基础自主梳理 温馨提示 二次函数y=x2+bx+c(呋0)的图象和性质如下表所示: 函数 y=x2+bx+c(a,b,c是常数,0) 图象 抛物线 a的取值 a>0 a<0 顶点坐标 b 4ac-b2 2a’4a 对称轴 直线丑 导航页
导航页 基础自主梳理 温馨提示 二次函数y=ax2+bx+c(a≠0)的图象和性质如下表所示: 函数 y=ax2 +bx+c(a,b,c 是常数,a≠0) 图象 抛物线 a 的取值 a>0 a<0 顶点坐标 − 𝐛 𝟐𝐚 , 𝟒𝐚𝐜−𝐛 𝟐 𝟒𝐚 对称轴 直线 x=- 𝐛 𝟐𝐚
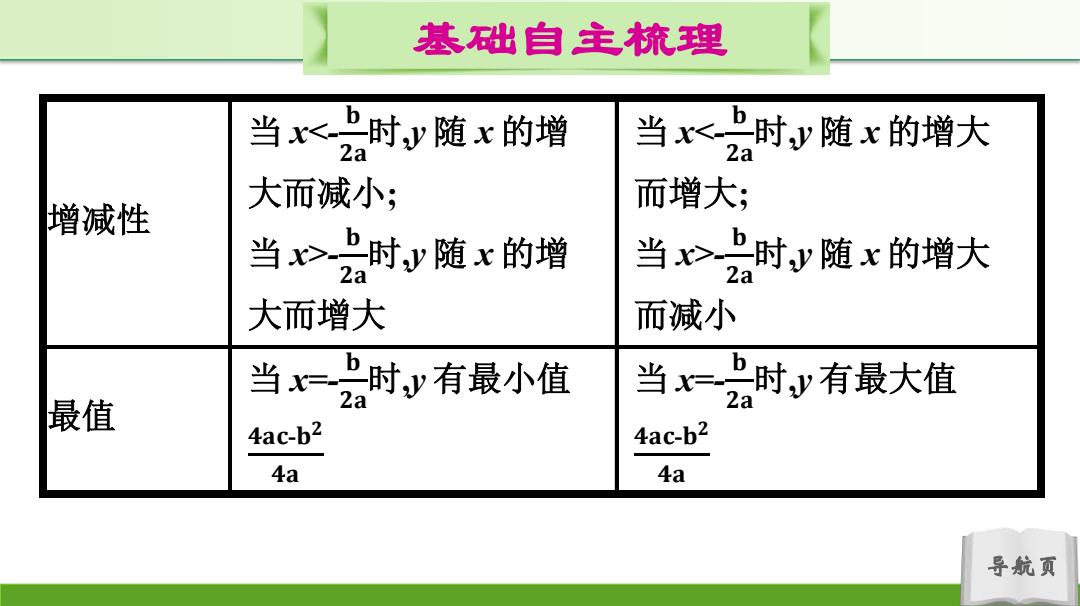
基础自主梳理 当<时y随x的增 当<时y随x的增大 2a 2a 大而减小; 而增大; 增减性 当之时y随x的增 当之时y随x的增大 2a 2a 大而增大 而减小 当=b时y有最小值 当=时y有最大值 最值 2a 4ac-b2 4ac-b2 4a 4a 导航页
导航页 基础自主梳理 增减性 当 x- 𝐛 𝟐𝐚 时,y 随 x 的增 大而增大 当 x- 𝐛 𝟐𝐚 时,y 随 x 的增大 而减小 最值 当 x=- 𝐛 𝟐𝐚 时,y 有最小值 𝟒𝐚𝐜-𝐛 𝟐 𝟒𝐚 当 x=- 𝐛 𝟐𝐚 时,y 有最大值 𝟒𝐚𝐜-𝐛 𝟐 𝟒𝐚

核心心重难探究 知识点一:二次函数y=x2+bx+c的图象与性质 【例1】已知函数y=c2-(2a+1)x-1(a是常数,0),下列结论 正确的是(D) A.当a=1时,函数图象经过(1,3) B.函数图象与y轴的交点坐标为(-1,0) C.若a>0,则当x≥1时y随x的增大而增大 D.若a<0,则当x≥1时y随x的增大而减小 思路点拨:根据二次函数的 可以判断各个选项中 的说法是否正确,确定出答案! 导航页
导航页 核心重难探究 知识点一:二次函数y=ax2+bx+c的图象与性质 【例1】已知函数y=ax2 -(2a+1)x-1(a是常数,a≠0),下列结论 正确的是( ). A.当a=1时,函数图象经过(1,3) B.函数图象与y轴的交点坐标为(-1,0) C.若a>0,则当x≥1时,y随x的增大而增大 D.若a<0,则当x≥1时,y随x的增大而减小 思路点拨:根据二次函数的 可以判断各个选项中 的说法是否正确,确定出答案. D

核心重难探究 【方法归纳】 解决这类问题的关键是明确题意,灵活运用二次函数的性质 解答. 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题的关键是明确题意,灵活运用二次函数的性质 解答

核心心重难探究 知识点二:二次函数y=x2+bx+c图象上点的坐标特征 【例2】已知抛物线y=x2-4x+c经过点(0,9). (1)求c的值; (2)若点A(3,y1),B(4y2)在该抛物线上,试比较y1y2的大小 思路点拨:(1)将经过的点(0,9)的坐标代入 求解 即可; (2)分别将点A,B的坐标代入 求出y1y2,比较大小 即可. 导航页
导航页 核心重难探究 知识点二:二次函数y=ax2+bx+c图象上点的坐标特征 【例2】已知抛物线y=x2 -4x+c经过点(0,9). (1)求c的值; (2)若点A(3,y1 ),B(4,y2 )在该抛物线上,试比较y1 ,y2的大小. 思路点拨:(1)将经过的点(0,9)的坐标代入 求解 即可; (2)分别将点A,B的坐标代入 求出y1 ,y2 ,比较大小 即可

核心重难探究 解:1).地物线y=x2-4x+c经过点(0,9), ‘.c=9. (2)y1=32-4×3+9=9-12+9=6y2=42-4×4+9=9, .6<9,∴y1<y2 【方法归纳】 比较函数值的大小用两种方法: ()先求出函数值,再比较大小; (2)先求出对称轴,再利用增减性比较大小 导航页
导航页 核心重难探究 解:(1)∵抛物线y=x2 -4x+c经过点(0,9), ∴c=9. (2)y1 =3 2 -4×3+9=9-12+9=6,y2 =4 2 -4×4+9=9, ∵6<9,∴y1<y2 . 【方法归纳】 比较函数值的大小用两种方法: (1)先求出函数值,再比较大小; (2)先求出对称轴,再利用增减性比较大小
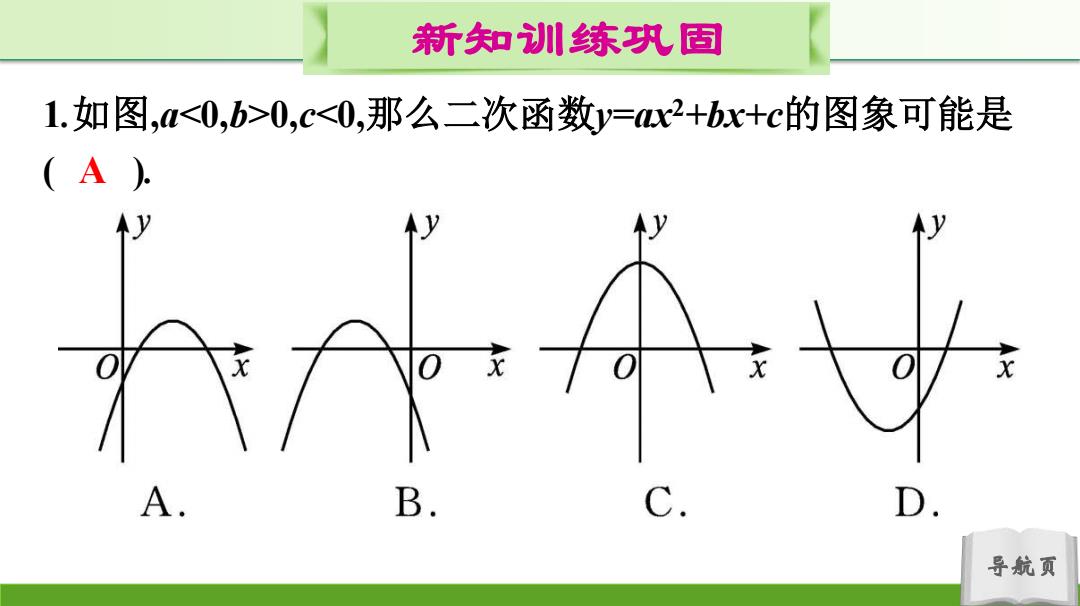
新知训练巩固 1.如图,M0,c<0,那么二次函数y=x2+bx+c的图象可能是 (A) A B D 导航页
导航页 新知训练巩固 1.如图,a0,c<0,那么二次函数y=ax2+bx+c的图象可能是 ( A )