
家庭们亚 5三角函数的应用 第2课时 仰角、俯角
5 三角函数的应用 第2课时 仰角、俯角

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
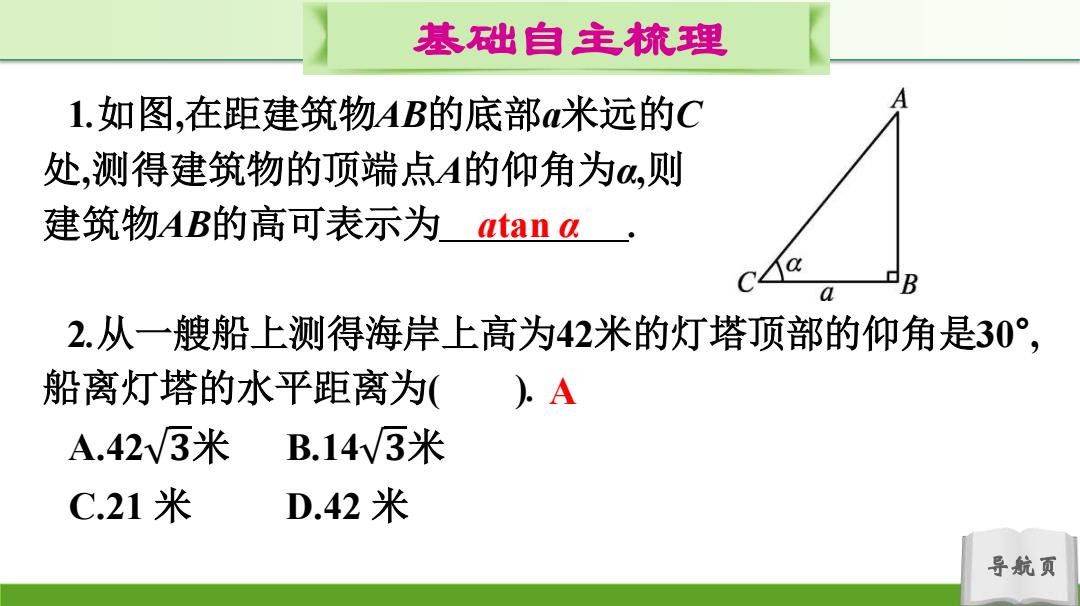
基础自主梳理 1.如图,在距建筑物AB的底部a米远的C 处,测得建筑物的顶端点A的仰角为a,则 建筑物AB的高可表示为tana Cd& B 2.从一艘船上测得海岸上高为42米的灯塔顶部的仰角是30°, 船离灯塔的水平距离为( ).A A.423米 B.14v3米 C.21米 D.42米 导航页
导航页 基础自主梳理 1.如图,在距建筑物AB的底部a米远的C 处,测得建筑物的顶端点A的仰角为α,则 建筑物AB的高可表示为 . 2.从一艘船上测得海岸上高为42米的灯塔顶部的仰角是30° , 船离灯塔的水平距离为( ). A.42 𝟑米 B.14 𝟑米 C.21 米 D.42 米 atan α A
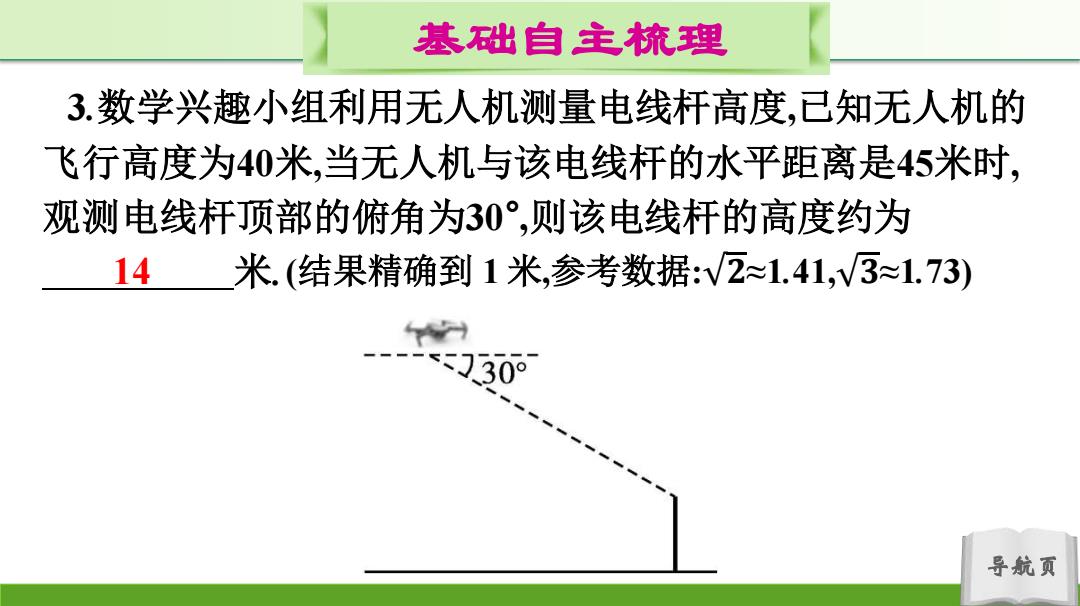
基础自主梳理 3.数学兴趣小组利用无人机测量电线杆高度,已知无人机的 飞行高度为40米,当无人机与该电线杆的水平距离是45米时, 观测电线杆顶部的俯角为30°,则该电线杆的高度约为 14 米.(结果精确到1米,参考数据:v2≈1.41,V3≈1.73) 30° 导航页
导航页 基础自主梳理 3.数学兴趣小组利用无人机测量电线杆高度,已知无人机的 飞行高度为40米,当无人机与该电线杆的水平距离是45米时, 观测电线杆顶部的俯角为30° ,则该电线杆的高度约为 14 米. (结果精确到 1 米,参考数据: 𝟐≈1.41, 𝟑≈1.73)

基础自主梳理 4.如图,甲楼AB的高度为20米,自甲楼楼顶A处,测得乙楼顶 端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼 CD的高度是(20+203)米 45 30° 甲B D乙 导航页
导航页 基础自主梳理 4.如图,甲楼AB的高度为20米,自甲楼楼顶A处,测得乙楼顶 端C处的仰角为45° ,测得乙楼底部D处的俯角为30° ,则乙楼 CD的高度是 (20+20 𝟑) 米

核心重难探究 知识点:仰角、俯角 【例题】小明利用寒假进行综合实践活动,他想 利用测角仪和卷尺测量自家所住楼(甲楼)与对面 邮政大楼(乙楼)的高度,现小明用卷尺测得甲楼宽 B 乙楼 甲楼 AE是8m,用测角仪在甲楼楼顶E处与A处测得乙楼顶部D的 仰角分别为37°和42°,同时在A处测得乙楼底部B处的俯角为 32°,请根据小明测得数据帮他计算甲、乙两幢楼的高度.(精 确到0.01m(参考数据:c0s32°≈0.85,tan32°≈0.62, c0s42°≈0.74,tan42°≈0.90,c0s37°≈0.80,tan37≈0.75) 导航页
导航页 核心重难探究 知识点:仰角、俯角 【例题】小明利用寒假进行综合实践活动,他想 利用测角仪和卷尺测量自家所住楼(甲楼)与对面 邮政大楼(乙楼)的高度,现小明用卷尺测得甲楼宽 AE是8 m,用测角仪在甲楼楼顶E处与A处测得乙楼顶部D的 仰角分别为37°和42° ,同时在A处测得乙楼底部B处的俯角为 32° ,请根据小明测得数据帮他计算甲、乙两幢楼的高度.(精 确到0.01 m)(参考数据:cos 32°≈0.85,tan 32°≈0.62, cos 42°≈0.74,tan 42°≈0.90,cos 37°≈0.80,tan 37°≈0.75)

核心重难探究 思路点拨:(1)怎样作辅助线构造直角三角形? (2)图中的基本图形有哪些?它们有哪些性质? 导航页
导航页 核心重难探究 思路点拨:(1)怎样作辅助线构造直角三角形? (2)图中的基本图形有哪些?它们有哪些性质?

核心重难探究 解:过点A作AN LBD于点N, 由题意,得∠DEN=37°,∠DAN=42°,∠NAB=32°. 在Rt△DNE中, tan∠DEN=tanm37°20.75 EN 设DN=3xm,则EN=4xm. 0 在Rt△DNA中,DN=3x,AN=4x-8, CF 楼 甲楼 :an∠DAN-tan4-2°即g9,解得=2 .∴.DN=36,AN=40. 导航页
导航页 核心重难探究 解:过点A作AN⊥BD于点N, 由题意,得∠DEN=37° ,∠DAN=42° ,∠NAB=32° . 在Rt△DNE中, tan∠DEN=tan 37° = 𝑫𝑵 𝑬𝑵 ≈0.75= 𝟑 𝟒 , 设DN=3x m,则EN=4x m. 在Rt△DNA中,DN=3x,AN=4x-8, ∵tan∠DAN=tan 42° = 𝑫𝑵 𝑨𝑵 ,即 𝟑𝒙 𝟒𝒙-𝟖 ≈0.9,解得 x=12. ∴DN=36,AN=40

核心重难探究 在RIABNA中,tan∠NAB=tan32°BN AN' .∴.BN=AN.tan32°≈24.8. .∴.DB=DN+BN=36+24.8=60.8,AC=BN=24.8. .∴.甲楼的高为24.8m,乙楼的高为60.8m. 导航页
导航页 核心重难探究 在 Rt△BNA 中,∵tan∠NAB=tan 32° = 𝑩𝑵 𝑨𝑵 , ∴BN=AN·tan 32°≈24.8. ∴DB=DN+BN=36+24.8=60.8,AC=BN=24.8. ∴甲楼的高为24.8 m,乙楼的高为60.8 m

核心重难探究 【方法归纳】 解决此类问题要了解角之间的关系,找到相关联的直角三角 形,当图形中没有直角三角形时,要通过作高或垂线构造直角 三角形,另当问题以一个实际问题的形式给出时,要善于读懂 题意,把实际问题划归为直角三角形中边角关系问题加以解 决 导航页
导航页 核心重难探究 【方法归纳】 解决此类问题要了解角之间的关系,找到相关联的直角三角 形,当图形中没有直角三角形时,要通过作高或垂线构造直角 三角形,另当问题以一个实际问题的形式给出时,要善于读懂 题意,把实际问题划归为直角三角形中边角关系问题加以解 决