
家庭缠亚 2 二次函数的图象与性质 第3课时 二次函数y=a(《-h)的图象与性质
2 二次函数的图象与性质 第3课时 二次函数y=a(x-h)2的图象与性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.二次函数y=2x2,y=2k-1)2,y=2(x+1)2的图象都是抛物线 并且形状相同,只是位置 不同.将函数y=2x2的图象向右 平移1个单位长度,就得到函数y=2(x-1)上的图象;将函数y=2x2 的图象向左平移1个单位长度,就得到函数y=2(x+1)2的图象 导航页
导航页 基础自主梳理 1.二次函数y=2x 2 ,y=2(x-1)2 ,y=2(x+1)2的图象都是 , 并且形状相同,只是 不同.将函数y=2x 2的图象向右 平移1个单位长度,就得到函数 的图象;将函数y=2x 2 的图象向左平移1个单位长度,就得到函数 的图象. 抛物线 位置 y=2(x-1)2 y=2(x+1)2

基础自主梳理 温馨提示 1.一般地,二次函数y=化-)的图象是抛物线,它与抛物线 y=x2的形状、开口方向和开口大小相同,只是在坐标系中的 位置不同.将抛物线y=2向左或向右平移个单位长度便得 到抛物线y=k-h)2当h>0时,向右平移;当<0时,向左平移. 导航页
导航页 基础自主梳理 温馨提示 1.一般地,二次函数y=a(x-h) 2的图象是抛物线,它与抛物线 y=ax2的形状、开口方向和开口大小相同,只是在坐标系中的 位置不同.将抛物线y=ax2向左或向右平移|h|个单位长度便得 到抛物线y=a(x-h) 2 .当h>0时,向右平移;当h<0时,向左平移
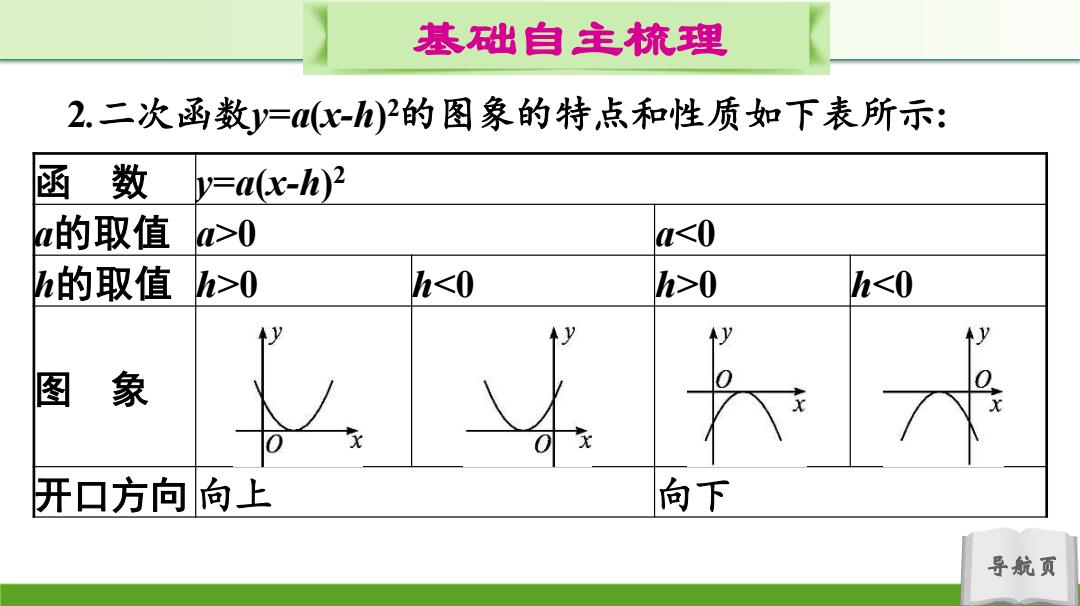
基础自主梳理 2.二次函数y=x)2的图象的特点和性质如下表所示: 函数 y=a(x-h)2 a的取值 a>0 a0 h0 h<0 y 个y 图象 开口方向向上 向下 导航页
导航页 基础自主梳理 2.二次函数y=a(x-h) 2的图象的特点和性质如下表所示: 函 数 y=a(x-h) 2 a的取值 a>0 a0 h0 h<0 图 象 开口方向 向上 向下

基础自主梳理 对称轴 直线x=h 顶点坐标 h,0) a的取值 a>0 ah时y随x的增大 当x>h时,y随x的增大而减小 而增大 导航页
导航页 基础自主梳理 对称轴 直线x=h 顶点坐标 (h,0) a的取值 a>0 ah时,y随x的增大 而增大 当xh时,y随x的增大而减小

基础自主梳理 2抛物线=-3)2的对称轴是直线x=3_,顶点坐标 是(3,0) 导航页
导航页 基础自主梳理 2.抛物线y= (x-3)2的对称轴是 ,顶点坐标 是 . 𝟏 𝟐 直线x=3 (3,0)

核心心重难探究 知识点一:二次函数y=ax-h)2的图象与性质 【例1】关于抛物线=x-1)2,下列说法错误的是(D) A.开口向上 B.与x轴只有一个交点 C.对称轴是直线x=1 D.当x>0时y随x的增大而增大 思路点拨:抛物线y=-)的顶,点坐标是 ,顶点在 轴上,对称轴是 导航页
导航页 核心重难探究 知识点一:二次函数y=a(x-h) 2的图象与性质 【例1】关于抛物线y= (x-1)2 ,下列说法错误的是( ). A.开口向上 B.与x轴只有一个交点 C.对称轴是直线x=1 D.当x>0时,y随x的增大而增大 思路点拨:抛物线y=a(x-h) 2的顶点坐标是 ,顶点在 轴上,对称轴是 . 𝟑 𝟒 D

核心重难探究 【方法归纳】 解决这类问题关键是掌握二次函数y=x-)的图象与性质, 数形结合求解即可 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题关键是掌握二次函数y=a(x-h) 2的图象与性质, 数形结合求解即可

核心重难探究 知识点二:二次函数y=x-)P图象上点的坐标特征 【例2】如图,抛物线y=2x-2)2与平行于x轴的直线交于点 A,B,抛物线的顶点为C,△ABC为等边三角形,求△ABC的面积 思路点拨:1)平行于x轴的直线AB有什么特征? (2)要想求出△ABC的面积需要知道哪些线段的长? 导航页
导航页 核心重难探究 知识点二:二次函数y=a(x-h) 2图象上点的坐标特征 【例2】如图,抛物线y=2(x-2)2与平行于x轴的直线交于点 A,B,抛物线的顶点为C,△ABC为等边三角形,求△ABC的面积. 思路点拨:(1)平行于x轴的直线AB有什么特征? (2)要想求出△ABC的面积需要知道哪些线段的长?