
家庭拿亚 4二次函数的应用 第2课时 ”利用二次丞数解快抛物线型问题
4 二次函数的应用 第2课时 利用二次函数解决抛物线型问题

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升
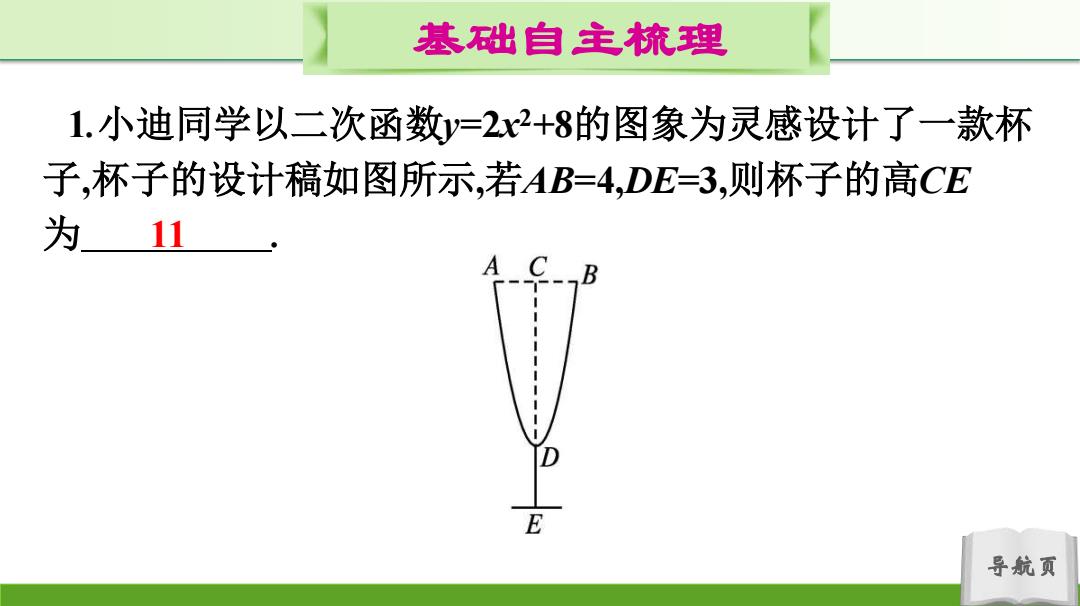
基础自主梳理 1.小迪同学以二次函数y=2x2+8的图象为灵感设计了一款杯 子,杯子的设计稿如图所示,若AB=4,DE=3,则杯子的高CE 为 11 A 导航页
导航页 基础自主梳理 1.小迪同学以二次函数y=2x 2+8的图象为灵感设计了一款杯 子,杯子的设计稿如图所示,若AB=4,DE=3,则杯子的高CE 为 11
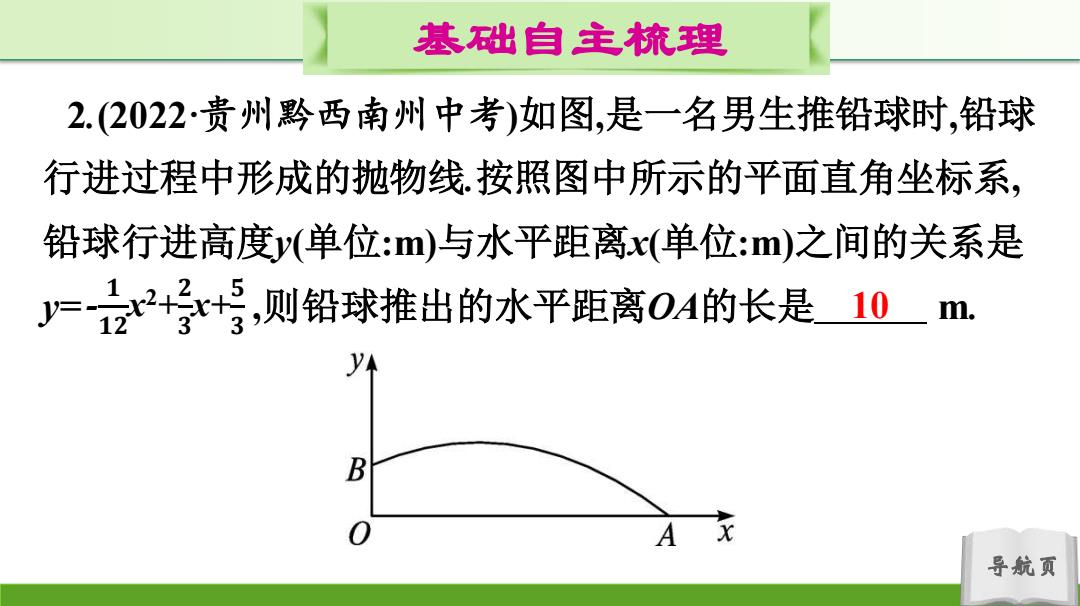
基础自主梳理 2.(2022贵州黔西南州中考)如图,是一名男生推铅球时,铅球 行进过程中形成的抛物线按照图中所示的平面直角坐标系, 铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 =2++号,则铅球推出的水平距离OA的长是 10m. y B A 导航页
导航页 基础自主梳理 2.(2022·贵州黔西南州中考)如图,是一名男生推铅球时,铅球 行进过程中形成的抛物线.按照图中所示的平面直角坐标系, 铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 y= - ,则铅球推出的水平距离OA的长是 m. 𝟏 𝟏𝟐 x 2 + 𝟐 𝟑 x+𝟓 𝟑 10

核心重难探究 知识点:“运动类”问题 【例题】如图,足球场上守门员在O处开出一高球,球从离 地面1米的A处飞出(A在轴上),运动员乙在距点O6米的B处 发现球在自己头的正上方达到最高点M,距地面约4米高,球落 地后又一次弹起,据实验测算,足球在草坪上弹起后的抛物线 与原来的抛物线形状相同,最大高度减少到原来最大高度的 一半 D 导航页
导航页 核心重难探究 知识点:“运动类”问题 【例题】如图,足球场上守门员在O处开出一高球,球从离 地面1米的A处飞出(A在y轴上),运动员乙在距点O 6米的B处 发现球在自己头的正上方达到最高点M,距地面约4米高,球落 地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线 与原来的抛物线形状相同,最大高度减少到原来最大高度的 一半

核心重难探究 (1)求足球开始飞出到第一次落地时,该抛物线的表达式; (2)足球第一次落地点C距守门员多少米?(取4V3≈7) (③)运动员乙要在第二个落地点D处抢到球,他应再向前跑多少 米?(取2V6≈5) 导航页
导航页 核心重难探究 (1)求足球开始飞出到第一次落地时,该抛物线的表达式; (2)足球第一次落地点 C 距守门员多少米?(取 4 𝟑≈7) (3)运动员乙要在第二个落地点 D 处抢到球,他应再向前跑多少 米?(取 2 𝟔≈5)

核心重难探究 思路点拨:(1)依题意设第一次落地时抛物线的表达式 为 ,把(0,1)代入即可求解; (2)令y=0可求出x的 个值,再按实际情况筛选; 3)本题有多种解法.如图可得第二次足球弹出后的距离为 CD,相当于将原抛物线向下平移了2个单位长度,可得2-立 6)2+4,解得x的值,即可知道CD,BD. 导航页
导航页 核心重难探究 思路点拨:(1)依题意设第一次落地时抛物线的表达式 为 ,把(0,1)代入即可求解; (2)令y=0可求出x的 个值,再按实际情况筛选; (3)本题有多种解法.如图可得第二次足球弹出后的距离为 CD,相当于将原抛物线向下平移了2个单位长度,可得2=- (x- 6)2 +4,解得x的值,即可知道CD,BD. 𝟏 𝟏𝟐

核心重难探究 解1)如图,设第一次落地时, 地物线的表达式为y=(c-6)2+4. 由已知,当x=0时y=1,即36+4=1, D 1 12 表达式为=2-62+4或=立2+x+1 2)冷0,即-62+40. 解得x1=4V3+6≈13,x2=-4v3+6<0(此时的负值,舍去) '.足球第一次落地距守门员约13米, 导航页
导航页 核心重难探究 解:(1)如图,设第一次落地时, 抛物线的表达式为y=a(x-6)2+4. 由已知,当x=0时,y=1,即36a+4=1, ∴a=- 𝟏 𝟏𝟐 . ∴表达式为 y=- 𝟏 𝟏𝟐 (x-6)2 +4 或 y=- 𝟏 𝟏𝟐 x 2 +x+1. (2)令 y=0,即- 𝟏 𝟏𝟐 (x-6)2 +4=0. 解得 x1=4 𝟑+6≈13,x2=-4 𝟑+6<0(此时的负值,舍去). ∴足球第一次落地距守门员约 13 米

核心心重难探究 (3)如图,第二次足球弹出后的距离为CD,根据题意CD=EF (即相当于将地物线AEMFC向下平移了2个单位), :2=x-62+4 解得x1=6-2v6,x2=6+2V6. ∴.CD=k1-x2=4V6≈10. .∴.BD=13-6+10=17(米). ‘.他应再向前跑17米 导航页
导航页 核心重难探究 (3)如图,第二次足球弹出后的距离为CD,根据题意CD=EF (即相当于将抛物线AEMFC向下平移了2个单位), ∴2=- 𝟏 𝟏𝟐 (x-6)2 +4. 解得 x1=6-2 𝟔,x2=6+2 𝟔. ∴CD=|x1-x2|=4 𝟔≈10. ∴BD=13-6+10=17(米). ∴他应再向前跑17米

核心重难探究 【方法归纳】 解决这类问题的关键是要有建模思想,将题目中的语句转化 为数学语言,这样才能较好地领会题意并运用自已的知识解 决问题 导航页
导航页 核心重难探究 【方法归纳】 解决这类问题的关键是要有建模思想,将题目中的语句转化 为数学语言,这样才能较好地领会题意并运用自己的知识解 决问题