
家庭猴伞 微专题三 圆中常见的铺功线的作法
微专题三 圆中常见的辅助线的作法

专题(一)作弦的垂线段构造直角三角形 1.有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽 AB=60m,水面到拱顶距离CD=18m,当雨季来临,水面到拱顶 距离为3.5m时需要采取紧急措施,当水面宽MN=32m时是 否需要采取紧急措施?请说明理由. M
专题(一) 作弦的垂线段构造直角三角形 1.有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽 AB=60 m,水面到拱顶距离CD=18 m,当雨季来临,水面到拱顶 距离为3.5 m时需要采取紧急措施,当水面宽MN=32 m 时是 否需要采取紧急措施?请说明理由
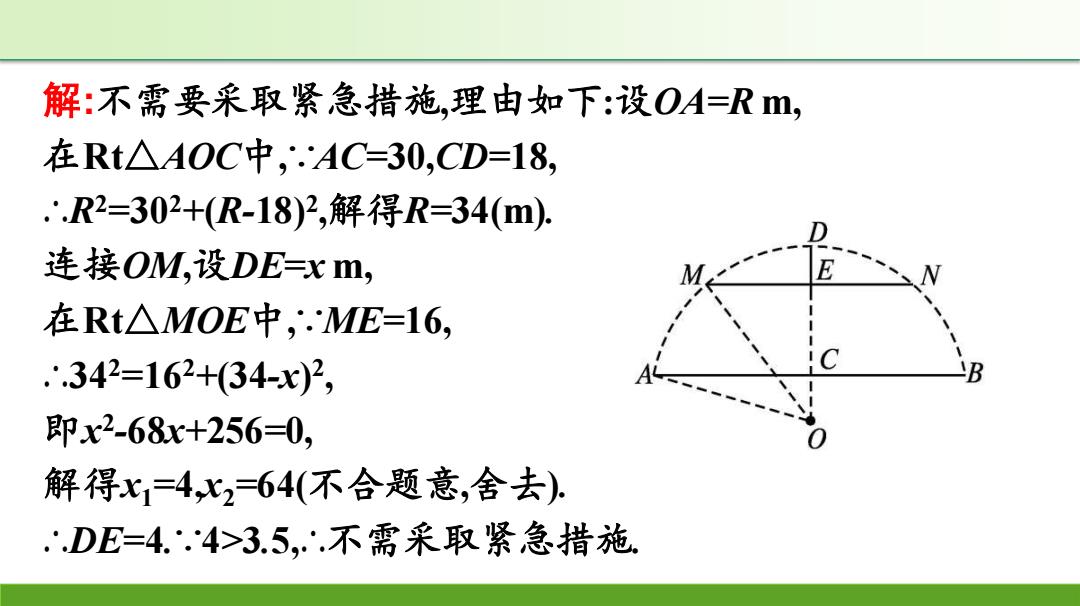
解:不需要采取紧急措施,理由如下:设OA=Rm, 在Rt△AOC中,∴.AC=30,CD=18, .∴R2=302+(R-18)2,解得R=34(m). 连接OM,设DE=xm, 在Rt△MOE中,.ME=16, ∴.342=162+34-x)2, 即x2-68x+256=0, 解得x1=4,x264(不合题意,舍去) ∴DE=4..4>3.5,.不需采取紧急措施
解:不需要采取紧急措施,理由如下:设OA=R m, 在Rt△AOC中,∵AC=30,CD=18, ∴R2=302+(R-18)2 ,解得R=34(m). 连接OM,设DE=x m, 在Rt△MOE中,∵ME=16, ∴342=162+(34-x) 2 , 即x 2 -68x+256=0, 解得x1 =4,x2 =64(不合题意,舍去). ∴DE=4.∵4>3.5,∴不需采取紧急措施
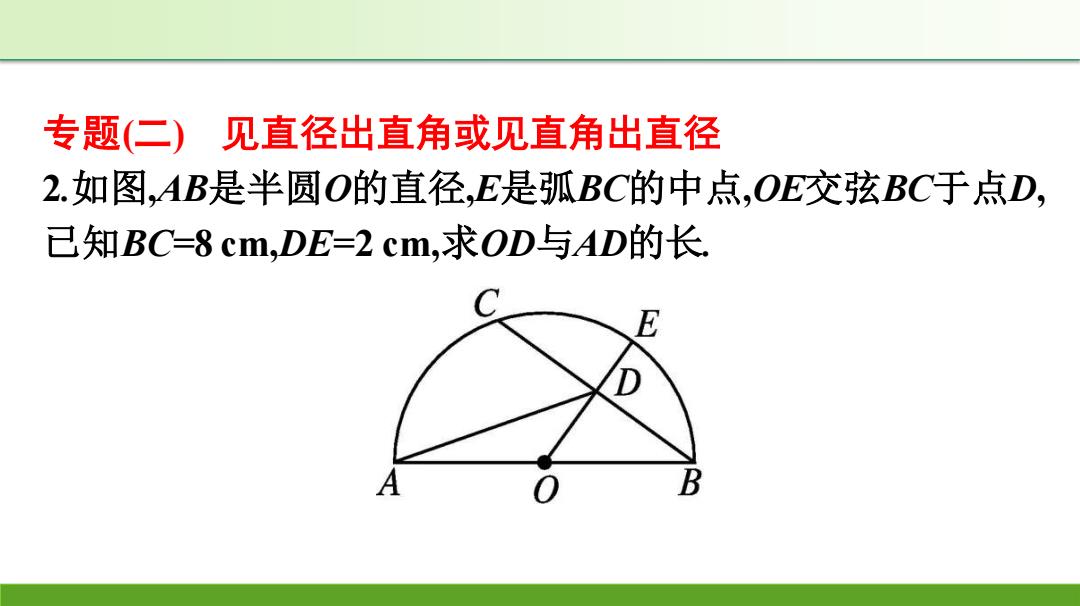
专题(二)」 见直径出直角或见直角出直径 2.如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D, 已知BC=8cm,DE=2cm,求OD与AD的长 E A B
专题(二) 见直径出直角或见直角出直径 2.如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D, 已知BC=8 cm,DE=2 cm,求OD与AD的长
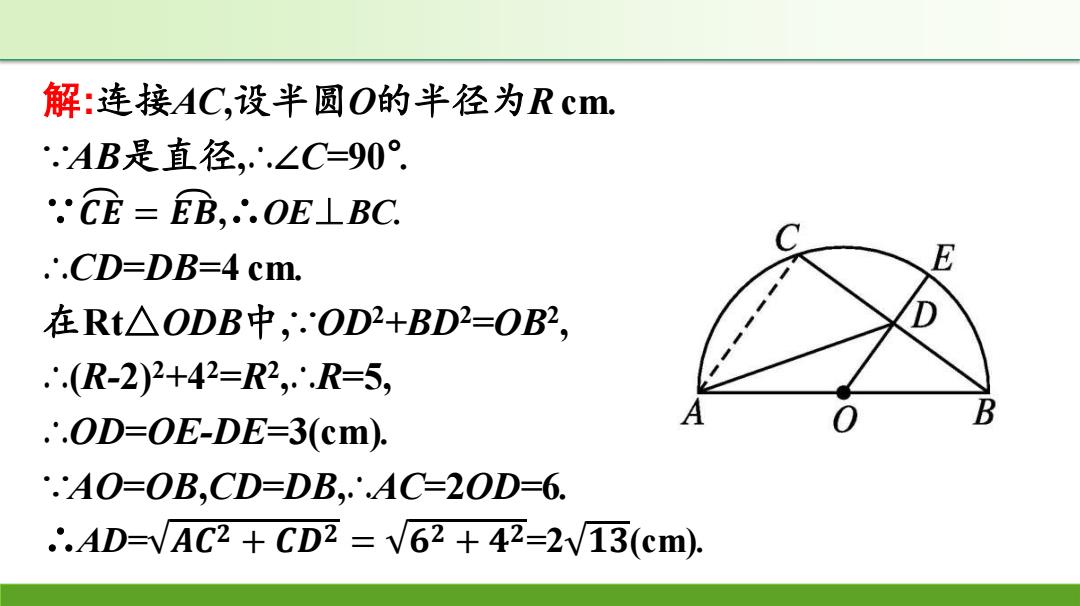
解:连接AC,设半圆O的半径为Rcm. .AB是直径,∴∠C=90° .CE=EB,∴.OE⊥BC C ..CD=DB=4 cm. E 在Rt△ODB中,∴.OD2+BD=OB2, D ∴.(R-2)2+42=R2,∴.R=5, .∴.OD=OE-DE=3(cm). A B .AO=OB,CD=DB,.AC=20D=6. .AD=VAC2+CD2=V62+42=2V13(cm
解:连接AC,设半圆O的半径为R cm. ∵AB是直径,∴∠C=90° . ∵𝑪 𝑬 = 𝑬 𝑩,∴OE⊥BC. ∴CD=DB=4 cm. 在Rt△ODB中,∵OD2+BD2=OB2 , ∴(R-2)2+4 2=R2 ,∴R=5, ∴OD=OE-DE=3(cm). ∵AO=OB,CD=DB,∴AC=2OD=6. ∴AD= 𝑨𝑪𝟐 + 𝑪𝑫𝟐 = 𝟔𝟐 + 𝟒𝟐 =2 𝟏𝟑(cm)

专题(三) 见切线连半径 3.如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线 PC,PD,切点分别为C,D,连接OP,CD. (1)求证:OP⊥CD; A (2)连接AD,BC,若∠DAB=50°, ∠CBA=70°,OA=2,求OP的长
专题(三) 见切线连半径 3.如图,AB是☉O的直径,过☉O外一点P作☉O的两条切线 PC,PD,切点分别为C,D,连接OP,CD. (1)求证:OP⊥CD; (2)连接AD,BC,若∠DAB=50° , ∠CBA=70° ,OA=2,求OP的长

(1)证明:连接OC,OD, PD,PC是回O的切线, .∴.∠ODP=∠OCP=90°. 在Rt△ODP和Rt△OCP中, .OD=OC,OP-OP, A .'.Rt△ODP≌Rt△OCP .∴.∠DOP=∠COP .OD=OC,..OP LCD
(1)证明:连接OC,OD, ∵PD,PC是☉O的切线, ∴∠ODP=∠OCP=90° . 在Rt△ODP和Rt△OCP中, ∵OD=OC,OP=OP, ∴Rt△ODP≌Rt△OCP. ∴∠DOP=∠COP. ∵OD=OC,∴OP⊥CD

(2)解:由题意知,OA=OD=0C=0B=2. ∴.∠ADO=∠DAO=50°,∠BCO=∠CBO=70°. ∴.∠AOD=80°,∠BOC=40°. .∴.∠COD=60° .OD=OC, .△COD是等边三角形 由(I)知,∠D0P=∠COP=30°,在Rt△ODP中,OP- OD 4v3 c0s30° = 3
(2)解:由题意知,OA=OD=OC=OB=2. ∴∠ADO=∠DAO=50° ,∠BCO=∠CBO=70° . ∴∠AOD=80° ,∠BOC=40° . ∴∠COD=60° . ∵OD=OC, ∴△COD是等边三角形. 由(1)知,∠DOP=∠COP=30° ,在 Rt△ODP 中,OP= 𝑶𝑫 𝐜𝐨𝐬𝟑𝟎° = 𝟒 𝟑 𝟑
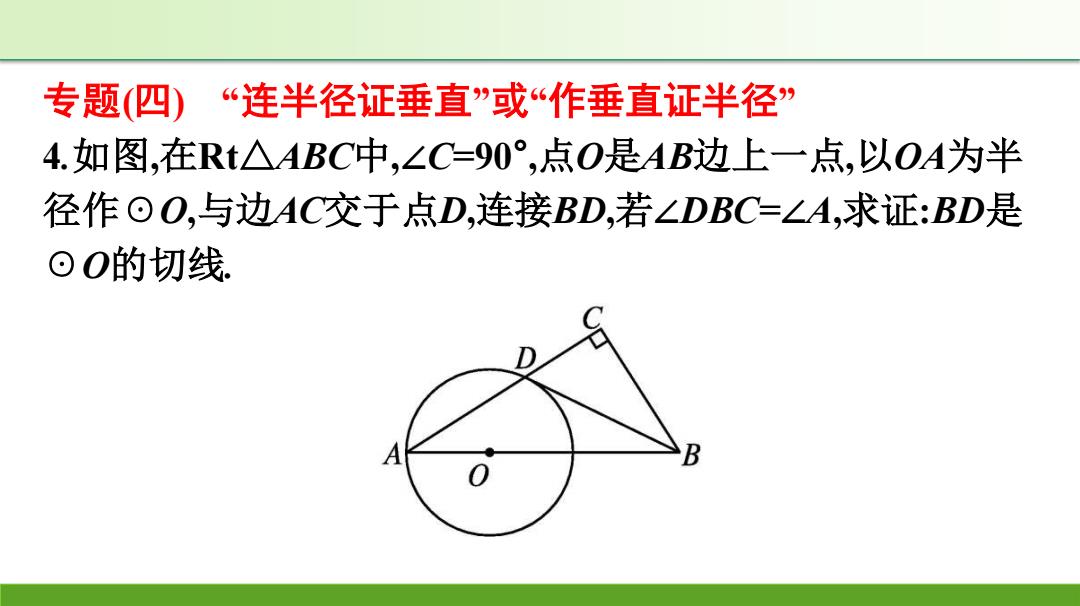
专题(四)“连半径证垂直”或“作垂直证半径” 4.如图,在Rt△ABC中,∠C=90°,点O是AB边上一点,以OA为半 径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是 ⊙O的切线 B
专题(四) “连半径证垂直”或“作垂直证半径” 4.如图,在Rt△ABC中,∠C=90° ,点O是AB边上一点,以OA为半 径作☉O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是 ☉O的切线
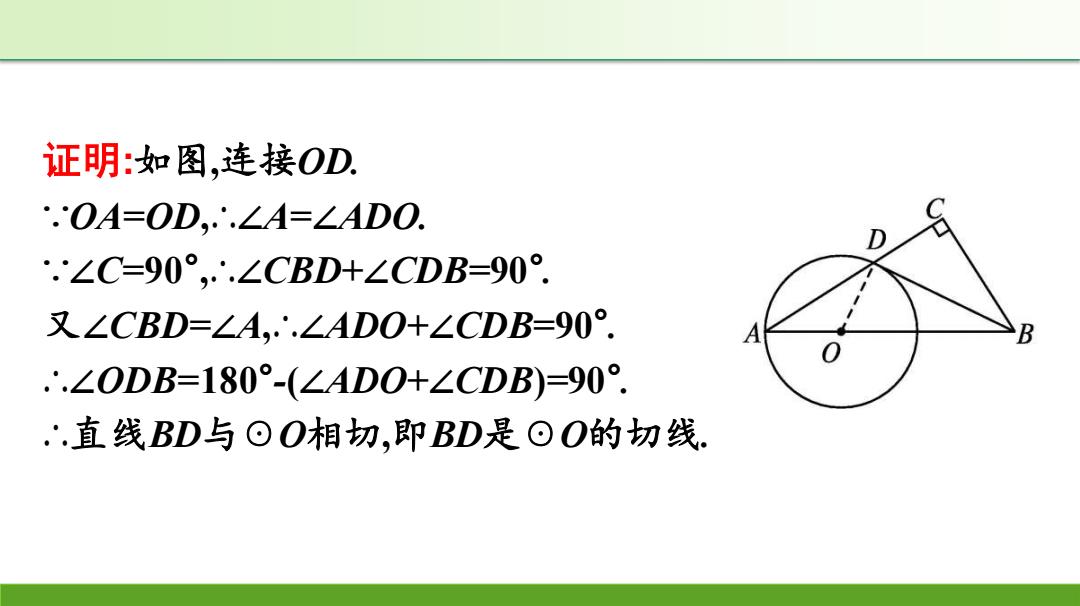
证明:如图,连接OD .OA=OD,∴.∠A=∠ADO. .'∠C=90°,∴.∠CBD+∠CDB=90°. 又∠CBD=∠A,∴∠ADO+∠CDB=90°. .∴.∠ODB=180°-(∠ADO+∠CDB)=90°. ∴.直线BD与⊙O相切,即BD是回O的切线
证明:如图,连接OD. ∵OA=OD,∴∠A=∠ADO. ∵∠C=90° ,∴∠CBD+∠CDB=90° . 又∠CBD=∠A,∴∠ADO+∠CDB=90° . ∴∠ODB=180°-(∠ADO+∠CDB)=90° . ∴直线BD与☉O相切,即BD是☉O的切线