
家庭拿亚 6 直线和圆的位置关系 第1课时 直线和圆的位置关系、切线的性质
6 直线和圆的位置关系 第1课时 直线和圆的位置关系、切线的性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.直线和圆有三种位置关系:相交、相切和相离, 2.直线与圆有唯一公共点(即直线和圆相切 )时,这条 直线叫做圆的切线,这个唯一的公共点叫做切点 3.设圆心O到直线的距离为d,圆O的半径为r,则有:直线和圆 相交,即d 导航页
导航页 基础自主梳理 1.直线和圆有三种位置关系: . 2.直线与圆有唯一公共点(即直线和圆 )时,这条 直线叫做圆的 ,这个唯一的公共点叫做 . 3.设圆心O到直线l的距离为d,圆O的半径为r,则有:直线和圆 相交,即d r;直线和圆相切,即d r;直线和 圆相离,即d r. 相交、相切和相离 相切 切线 切点

基础自主梳理 温馨提示 1.切线的性质可总结如下: 如果一条直线符合下列三个条件中的任意两个,那么它一定 满足第三个条件,这三个条件是:1)直线过圆心;2)直线过切 点;3)直线与圆的切线垂直 2.若出现圆的切线,则必连过切点的半径,得出垂直关系.简 记作:见切点,连半径,见垂直 导航页
导航页 基础自主梳理 温馨提示 1.切线的性质可总结如下: 如果一条直线符合下列三个条件中的任意两个,那么它一定 满足第三个条件,这三个条件是:(1)直线过圆心;(2)直线过切 点;(3)直线与圆的切线垂直. 2.若出现圆的切线,则必连过切点的半径,得出垂直关系.简 记作:见切点,连半径,见垂直
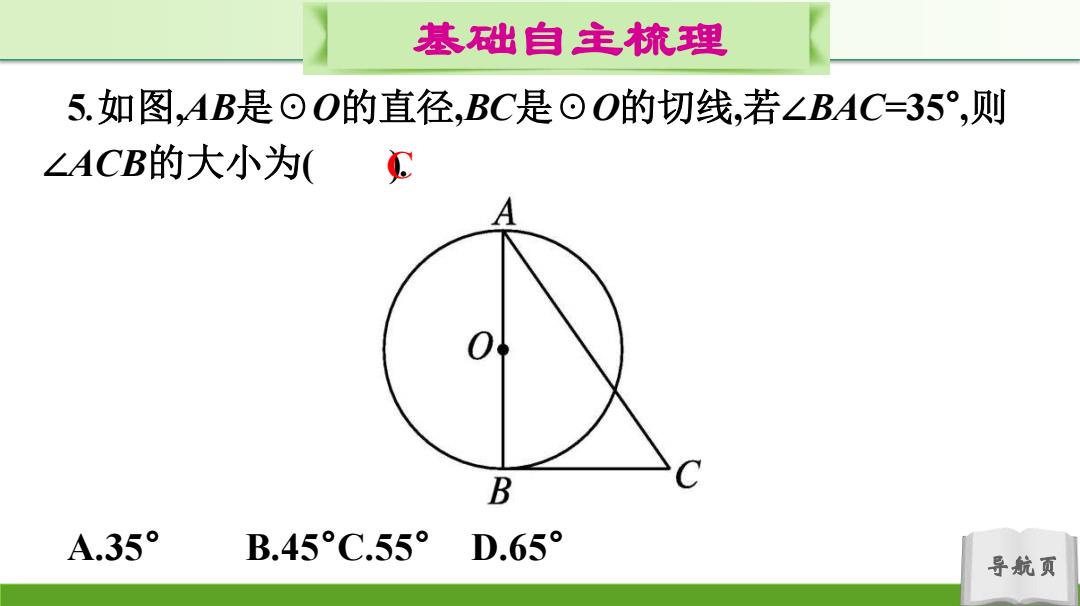
基础自主梳理 5.如图,AB是⊙O的直径,BC是⊙O的切线,若∠BAC=35°,则 ∠ACB的大小为( 04 B C A.35° B.45°C.55° D.65° 导航页
导航页 基础自主梳理 5.如图,AB是☉O的直径,BC是☉O的切线,若∠BAC=35° ,则 ∠ACB的大小为( ). A.35° B.45°C.55° D.65° C

核心重难探究 知识点一:直线与圆的位置关系 【例1】已知⊙O的半径为5,且圆心O到直线的距离d=2sin 30°+√引-2引,则直线l与圆的位置关系是(C) A.相交B.相切 C.相离D.无法确定 思路点拨:先求出 的值,再根据直线与圆的位置 关系求解即可」 导航页
导航页 核心重难探究 知识点一:直线与圆的位置关系 【例1】已知☉O的半径为5,且圆心O到直线l的距离d=2sin 30°+ +|-2|,则直线l与圆的位置关系是( ). A.相交 B.相切 C.相离 D.无法确定 思路点拨:先求出 的值,再根据直线与圆的位置 关系求解即可. 𝟗 C

核心重难探究 【方法归纳】 设⊙O的半径为r,圆心O到直线的距离为山,则直线与圆的位 置关系可以归纳为:(1)直线和⊙O相交台<;2)直线和⊙O 相切台=3)直线和⊙O相离台心: 导航页
导航页 核心重难探究 【方法归纳】 设☉O的半径为r,圆心O到直线l的距离为d,则直线与圆的位 置关系可以归纳为:(1)直线l和☉O相交⇔dr
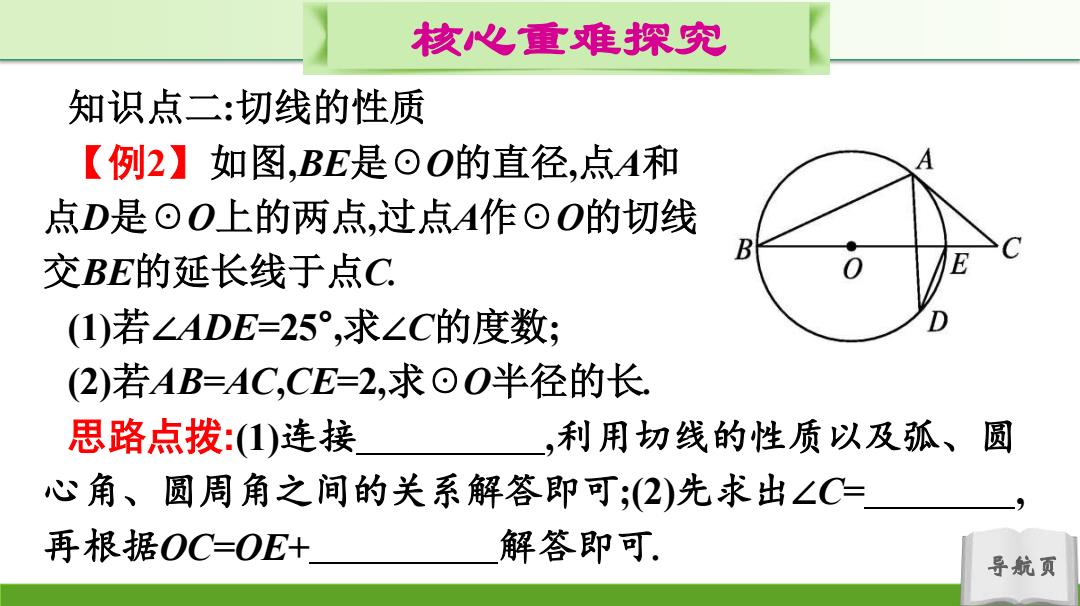
核心重难探究 知识点二:切线的性质 【例2】如图,BE是⊙O的直径,点A和 点D是⊙O上的两点,过点A作⊙O的切线 B 交BE的延长线于点C (1)若∠ADE=25°,求∠C的度数; (2)若AB=AC,CE=2,求⊙O半径的长 思路点拨:(1)连接 ,利用切线的性质以及孤、圆 心角、圆周角之间的关系解答即可;2)先求出∠C= 再根据OC=OE+ 解答即可 导航页
导航页 核心重难探究 知识点二:切线的性质 【例2】如图,BE是☉O的直径,点A和 点D是☉O上的两点,过点A作☉O的切线 交BE的延长线于点C. (1)若∠ADE=25° ,求∠C的度数; (2)若AB=AC,CE=2,求☉O半径的长. 思路点拨:(1)连接 ,利用切线的性质以及弧、圆 心角、圆周角之间的关系解答即可;(2)先求出∠C= , 再根据OC=OE+ 解答即可
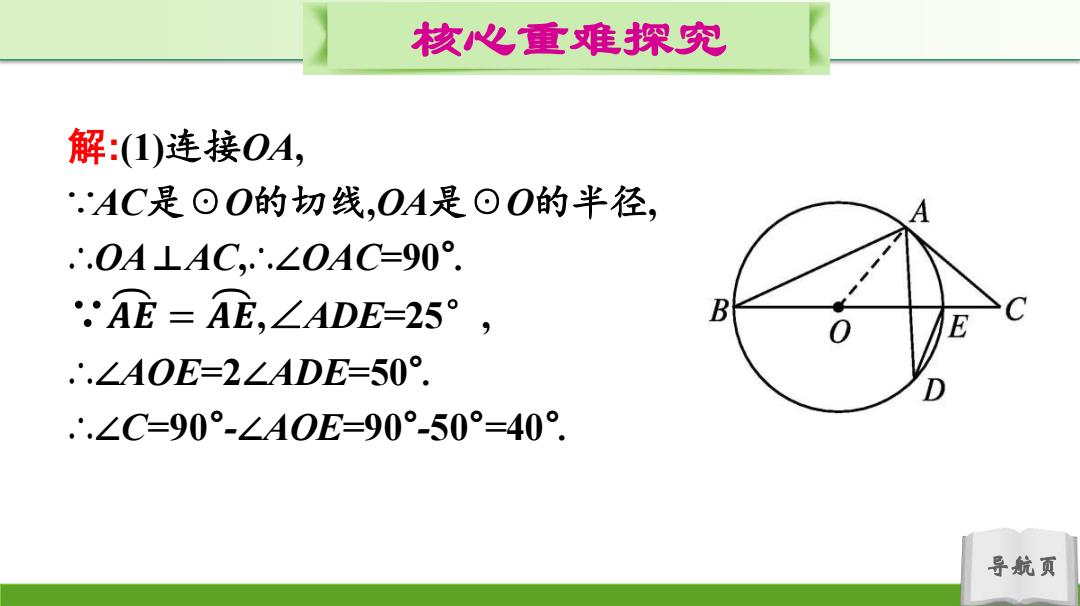
核心重难探究 解:(1)连接OA, .AC是⊙O的切线,OA是回O的半径, A .∴.OA LAC,∴.∠OAC=90° ①E=AE,∠ADE=25°, B E .∴.∠AOE=2∠ADE=50°. .∴.∠C=90°-∠A0E=90°-50°=40°. 导航页
导航页 核心重难探究 解:(1)连接OA, ∵AC是☉O的切线,OA是☉O的半径, ∴OA⊥AC,∴∠OAC=90° . ∵𝑨 𝑬 = 𝑨 𝑬,∠ADE=25° , ∴∠AOE=2∠ADE=50° . ∴∠C=90°-∠AOE=90°-50° =40°

核心重难探究 2).AB=AC,∴.∠B=∠C .AE=AE,∴.∠AOC=2∠B. .∴.∠AOC=2∠C .∠OAC=90°,∴.∠AOC+∠C=90°. 3∠C-90°,解得∠C=30°..01=20C 设⊙0的半径为, CE=2,之+2),解得=2..⊙0的半径为2. 导航页
导航页 核心重难探究 (2)∵AB=AC,∴∠B=∠C. ∵𝑨 𝑬 = 𝑨 𝑬,∴∠AOC=2∠B. ∴∠AOC=2∠C. ∵∠OAC=90° ,∴∠AOC+∠C=90° . ∴3∠C=90°,解得∠C=30°.∴OA=𝟏 𝟐 OC. 设☉O 的半径为 r, ∵CE=2,∴r= 𝟏 𝟐 (r+2),解得 r=2.∴☉O 的半径为 2