
家庭拿四 2 二次函数的图象与性质 第2课时 二次函数y=ax2+k的图象与性质
2 二次函数的图象与性质 第2课时 二次函数y=ax2+k的图象与性质

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.二次函数y=2x2,y=2x2+1y=2x2-1的图象都是抛物线,并且 形状相同,只是位置不同.将函数y=2x2的图象向上平 移1个单位长度,就得到函数y=2x2+1的图象;将函数y=2x2的 图象向下平移1个单位长度,就得到函数y=2x21的图象. 温馨提示 1.一般地,二次函数y=x2+k的图象是抛物线,它与抛物线 y=心2的形状、开口方向和开口大小相同,只是在坐标系中的 位置不同.将地物线y=2向上或向下平移k个单位长度便得 到抛物线y=2+k.当k>0时,向上平移;当k<0时,向下平移, 导航页
导航页 基础自主梳理 1.二次函数y=2x 2 ,y=2x 2+1,y=2x 2 -1的图象都是抛物线,并且 形状 ,只是 不同.将函数y=2x 2的图象向上平 移1个单位长度,就得到函数 的图象;将函数y=2x 2的 图象向下平移1个单位长度,就得到函数 的图象. 温馨提示 1.一般地,二次函数y=ax2+k的图象是抛物线,它与抛物线 y=ax2的形状、开口方向和开口大小相同,只是在坐标系中的 位置不同.将抛物线y=ax2向上或向下平移|k|个单位长度便得 到抛物线y=ax2+k.当k>0时,向上平移;当k<0时,向下平移. 相同 位置 y=2x 2+1 y=2x 2 -1
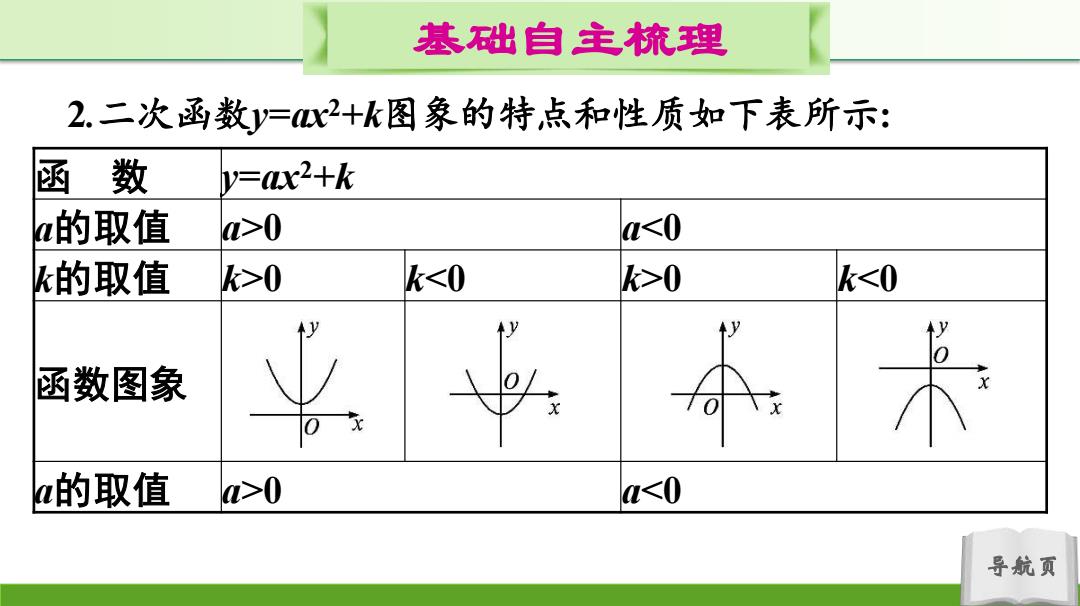
基础自主梳理 2.二次函数y=x2+k图象的特点和性质如下表所示: 函数 y=ax2+k a的取值 >0 a0 k0 k0 a<0 导航页
导航页 基础自主梳理 2.二次函数y=ax2+k图象的特点和性质如下表所示: 函 数 y=ax2+k a的取值 a>0 a0 k0 k0 a<0

基础自主梳理 开口方向 向上 向下 对称轴 y轴 顶点坐标 (0,k) 当x=0时,函数有最 函数最值 当x=0时,函数有最大值为k 小值为k 当x0时y随x的增 当x>h时,y随x的增大而减 大而增大 小 导航页
导航页 基础自主梳理 开口方向 向上 向下 对称轴 y轴 顶点坐标 (0,k) 函数最值 当x=0时,函数有最 小值为k 当x=0时,函数有最大值为k 函数增减性 当x0时,y随x的增 大而增大 当xh时,y随x的增大而减 小

基础自主梳理 2.抛物线y=2x2.1的顶点坐标是(0,-1) 导航页
导航页 基础自主梳理 2.抛物线y=2x 2 -1的顶点坐标是 (0,-1)

核心心重难探究 知识点一:二次函数y=x2+k的图象与性质 【例1】关于二次函数y=2x2+3,下列说法正确的是(B) A.图象的开口方向是向下 B.当x<-1时y随x的增大而减小 C.图象的顶点坐标是(2,3) D.当x=0时,y有最大值是3 思路点拨:分别利用二次函数的图象与 分析得出即 可. 导航页
导航页 核心重难探究 知识点一:二次函数y=ax2+k的图象与性质 【例1】关于二次函数y=2x 2+3,下列说法正确的是( ). A.图象的开口方向是向下 B.当x<-1时,y随x的增大而减小 C.图象的顶点坐标是(2,3) D.当x=0时,y有最大值是3 思路点拨:分别利用二次函数的图象与 分析得出即 可. B

核心重难探究 【方法归纳】 这类问题通常是利用数形结合思想求解,关键是掌握二次函 数y=x2+k的图象与性质. 导航页
导航页 核心重难探究 【方法归纳】 这类问题通常是利用数形结合思想求解,关键是掌握二次函 数y=ax2+k的图象与性质

核心心重难探究 知识点二:二次函数y=x2+k图象上点的坐标特征 【例2】已知点P(1,-2)在二次函数y=2+6的图象上,并且 点P关于x轴的对称点在反比例函数y=k的图象上 ()求此二次函数和反比例函数的表达式; (2)点(-1,4)是否同时在(1)中的两个函数图象上?请说明理由. 思路点拨:()怎样求出的值?关于x轴对称的点的坐标有什 么特征? (2)怎么判断所给的点是否在函数图象上? 导航页
导航页 核心重难探究 知识点二:二次函数y=ax2+k图象上点的坐标特征 【例2】已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且 点P关于x轴的对称点在反比例函数y= 的图象上. (1)求此二次函数和反比例函数的表达式; (2)点(-1,4)是否同时在(1)中的两个函数图象上?请说明理由. 思路点拨:(1)怎样求出a的值?关于x轴对称的点的坐标有什 么特征? (2)怎么判断所给的点是否在函数图象上? 𝒌 𝒙

核心重难探究 解:1).点P1,-2在二次函数y=x2+6的图象上, .‘.-21=a+6,解得1=-2. 点P为(1,4),所求二次函数表达式为y=-2x2+6. .点P关于x轴对称点的坐标为(1,4), “仁4,则所求反比例函数表达式为 导航页
导航页 核心重难探究 解:(1)∵点P(1,-2a)在二次函数y=ax2+6的图象上, ∴-2a=a+6,解得a=-2. ∴点P为(1,4),所求二次函数表达式为y=-2x 2+6. ∵点P关于x轴对称点的坐标为(1,-4), ∴k=-4,则所求反比例函数表达式为 y=- 𝟒 𝒙