
家庭值亚 第2课时 反比例数的性质
第2课时 反比例函数的性质

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基出自住梳理 1.反比例函数y=二的图象,当心0时,在每一象限内,y的值随x 值的增大而 ;当k<0时,在每一象限内,y的值随x值的增 大而 名师指导 1.同其图象的位置一样,反比例函数的增减性是由比例系数 k的符号决定的,反之,由反比例函数的增减性也可以判断k的 符号. 2.反比例函数的增减性,只能在每个象限内讨论
基础自主梳理 1.反比例函数 的图象,当k>0时,在每一象限内,y的值随x 值的增大而减小 ;当k<0时,在每一象限内,y的值随x值的增 大而增大 . y= 𝒌 𝒙 名师指导 1.同其图象的位置一样,反比例函数的增减性是由比例系数 k的符号决定的,反之,由反比例函数的增减性也可以判断k的 符号. 2.反比例函数的增减性,只能在每个象限内讨论

2.反比例函数yk(0)中系数k的几何意义 在反比例函数的图象上,过任一点Px,y)作x轴、y轴的 垂线PM,PN,垂足分别为M,N,则S矩形PwoN=PMOM=Kyl =xy=;SAPOM-SAPON-
2.反比例函数 y= 𝒌 𝒙 (k≠0)中系数 k 的几何意义 在反比例函数的图象上,过任一点 P(x,y)作 x 轴、y 轴的 垂线 PM,PN,垂足分别为 M,N,则 S 矩形 PMON=PM·OM=|x|·|y| =|xy|=|k| ;S△POM=S△PON= 𝟏 𝟐 |k|

温馨提示 根据反比例函数表达式的一搬形式一40,易变形得乘 积形式y=k(0),从而可知,其图象上任意一点的横、纵坐标 之积等于常数k根据这一特性,可得其几何意义应用该性质, 可以巧妙简捷地解决反比例函数图象与面积相关的诸多问题
温馨提示 根据反比例函数表达式的一般形式 (k≠0),易变形得乘 积形式xy=k(k≠0),从而可知,其图象上任意一点的横、纵坐标 之积等于常数k.根据这一特性,可得其几何意义.应用该性质, 可以巧妙简捷地解决反比例函数图象与面积相关的诸多问题. y= 𝒌 𝒙

核心重难探究 知识点 反比例函数的性质 【例题】若点44y,B-3y2),C(13)都在反比例函数= 3 的图象上,则y1y2y3的大小关系是(B). A.V2<V3 B.V3<V1<V2 C.V<23 D.V3<v2<1 思路点拨:(1)如何求得y1y2y3的大小? (2)利用反比例函数的图象和增减性如何比较y1y23的大小?
核心重难探究 知识点 反比例函数的性质 【例题】若点A(-4,y1 ),B(-3,y2 ),C(1,y3 )都在反比例函数 的图象上,则y1 ,y2 ,y3的大小关系是( ). A.y2<y1<y3 B.y3<y1<y2 C.y1<y2<y3 D.y3<y2<y1 思路点拨:(1)如何求得y1 ,y2 ,y3的大小? (2)利用反比例函数的图象和增减性如何比较y1 ,y2 ,y3的大小? B y=- 𝟑 𝒙

答案反比创函袅y冲重=30, 函数图象的两个分式分别位于二、四象限,且在每一象限内 y随x的增大而增大 -40,∴点C(1y3)位于第四象限, y3<0,y3<y1<y2故选B. 合
答案:∵反比例函数 中k=-30,∴点C(1,y3 )位于第四象限, ∴y3<0,∴y3<y1<y2 .故选B. y=- 𝟑 𝐱

【方法归纳】 解决该类问题的方法较多,一般来说,图象法形象直观,具有 一般性;特殊值法简单,它对于解答许多选择题都很有成效,应 学会灵活运用.在利用反比例函数的增减性比较大小时,一定 要看清是不是同一分支上的点,否则应分点在同一个象限与 不同象限两种情况讨论求解
【方法归纳】 解决该类问题的方法较多,一般来说,图象法形象直观,具有 一般性;特殊值法简单,它对于解答许多选择题都很有成效,应 学会灵活运用.在利用反比例函数的增减性比较大小时,一定 要看清是不是同一分支上的点,否则应分点在同一个象限与 不同象限两种情况讨论求解

新知训练织固 1.(2021贵州黔西南州模拟)对于反比例函数=5,下列说法错 误的是(C), A.图象经过点(1,-5) B.图象位于第二、第四象限 C.当x0时y随x的增大而增大
新知训练巩固 1.(2021·贵州黔西南州模拟)对于反比例函数 ,下列说法错 误的是( ). A.图象经过点(1,-5) B.图象位于第二、第四象限 C.当x0时,y随x的增大而增大 y=- 𝟓 𝒙 C
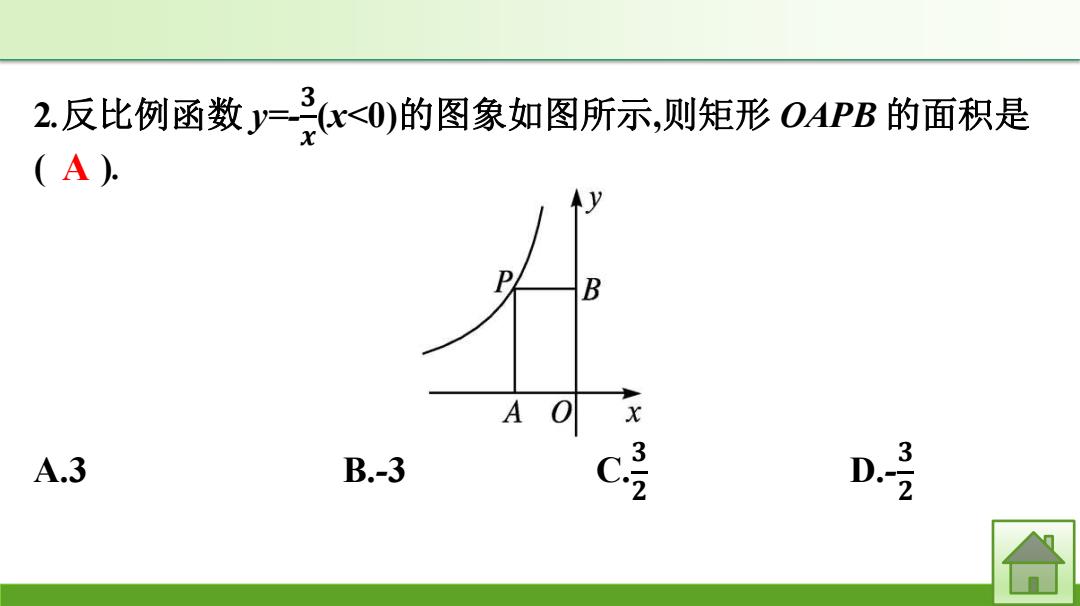
2.反比例函数一3<0)的图象如图所示,则矩形04PB的面积是 (A) B A 3 A.3 B.-3 3 D -2
2.反比例函数 y=- 𝟑 𝒙 (x<0)的图象如图所示,则矩形 OAPB 的面积是 ( ). A.3 B.-3 C. 𝟑 𝟐 D.- 𝟑 𝟐 A