
家庭猴伞 第3课时 三角形相似的判定条件(③)
第3课时 三角形相似的判定条件(3)

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.三角形相似的判定定理 三边 的两个三角形相似 名师指导 1.判断三边是否对应成比例的一般方法:(1)将三角形的边按 长度大小顺序排列;(2)分别计算对应边的比值;3)通过比值是 否相等来判断是否对应成比例. 2.该判定方法和全等三角形的判定方法“SSS”类似
基础自主梳理 1.三角形相似的判定定理 三边成比例 的两个三角形相似. 名师指导 1.判断三边是否对应成比例的一般方法:(1)将三角形的边按 长度大小顺序排列;(2)分别计算对应边的比值;(3)通过比值是 否相等来判断是否对应成比例. 2.该判定方法和全等三角形的判定方法“SSS”类似
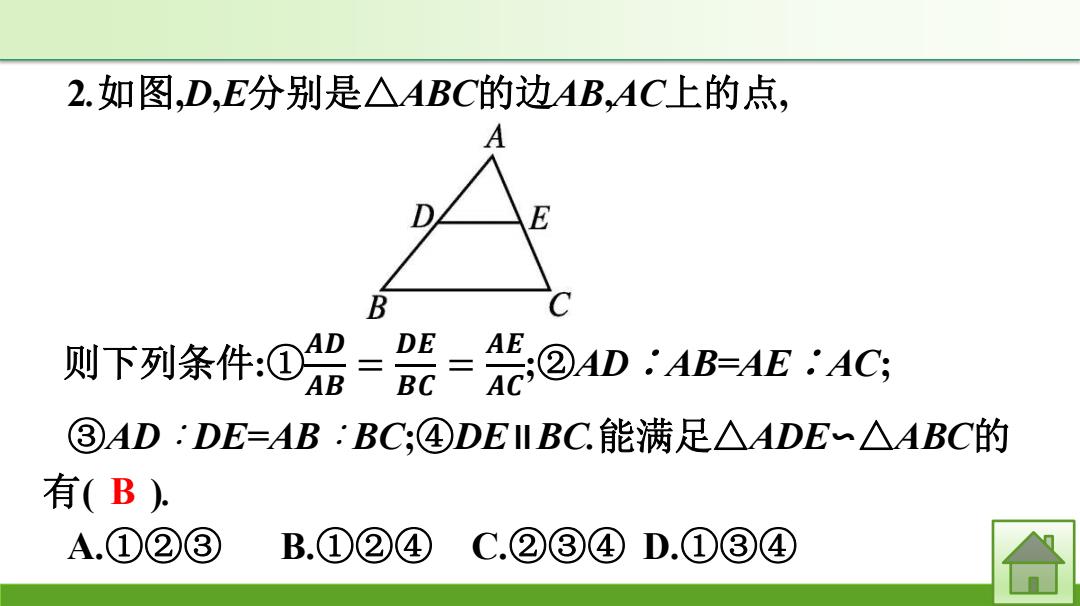
2.如图,D,E分别是△ABC的边AB,AC上的点, A E 则下列条件:@0= E AB BC ②AD:AB=AE:AC ③AD:DE=AB:BC,④DE II BC.能满足△ADE~△ABC的 有(B). A.①②③ B.①②④C.②③④D.①③④
2.如图,D,E分别是△ABC的边AB,AC上的点, 则下列条件:① 𝑨𝑫 𝑨𝑩 = 𝑫𝑬 𝑩𝑪 = 𝑨𝑬 𝑨𝑪 ;②AD∶AB=AE∶AC; ③AD∶DE=AB∶BC;④DE∥BC.能满足△ADE∽△ABC的 有( ). A.①②③ B.①②④ C.②③④ D.①③④ B
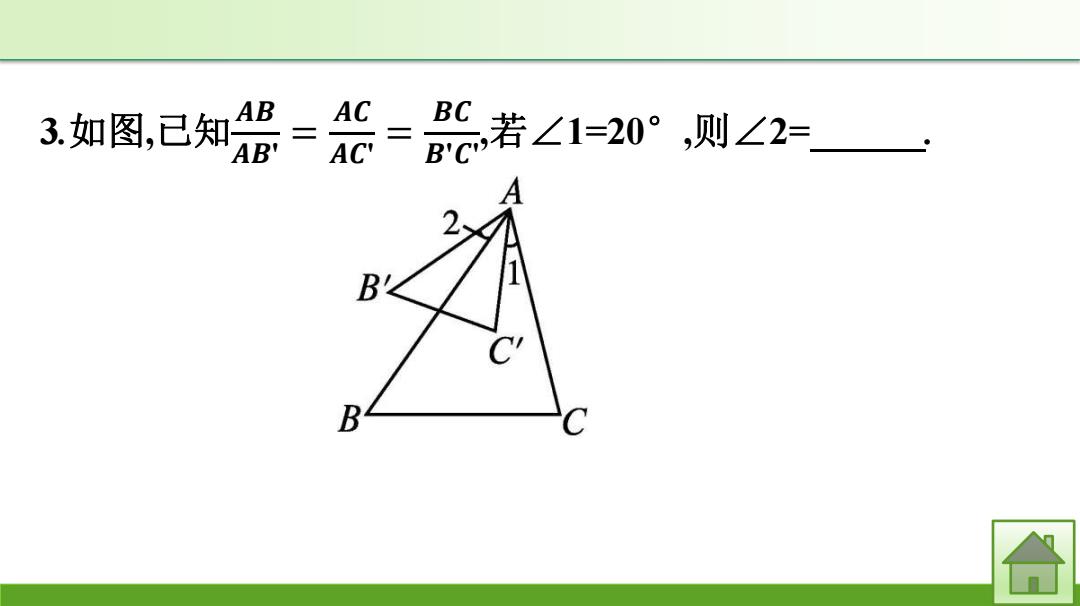
3如图,已知侣 怨= 若∠1=-20°,则∠2= BC B B C
3.如图,已知𝑨𝑩 𝑨𝑩' = 𝑨𝑪 𝑨𝑪' = 𝑩𝑪 𝑩'𝑪' ,若∠1=20° ,则∠2=20°
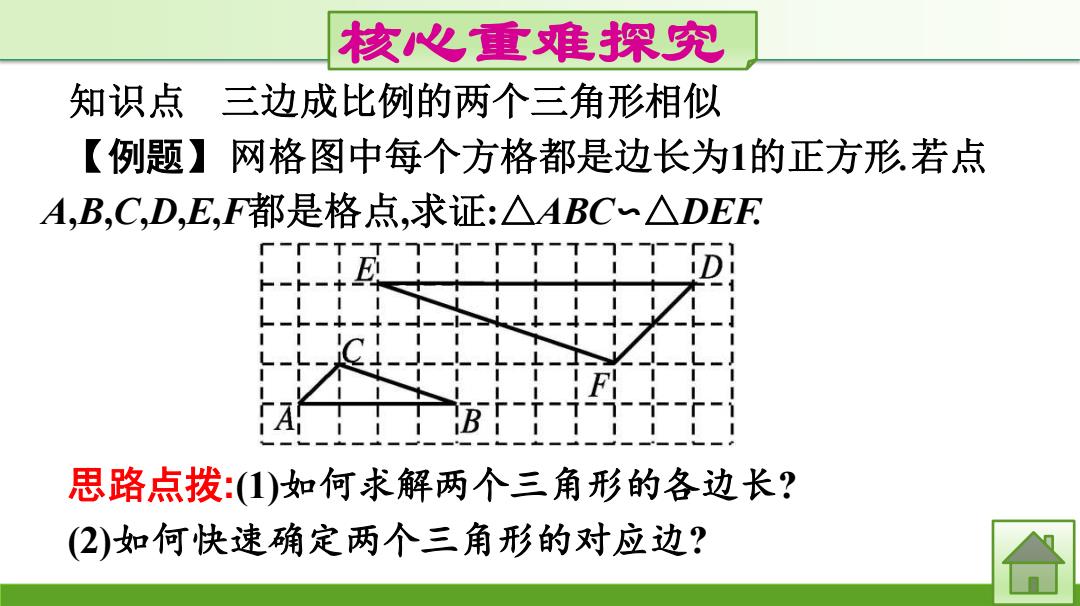
核心重难探究 知识点 三边成比例的两个三角形相似 【例题】网格图中每个方格都是边长为1的正方形.若点 A,B,C,D,E,F都是格点,求证:△ABC~△DEF E 思路点拨:1)如何求解两个三角形的各边长? (2)如何快速确定两个三角形的对应边?
核心重难探究 知识点 三边成比例的两个三角形相似 【例题】网格图中每个方格都是边长为1的正方形.若点 A,B,C,D,E,F都是格点,求证:△ABC∽△DEF. 思路点拨:(1)如何求解两个三角形的各边长? (2)如何快速确定两个三角形的对应边?

证明:由勾股定理,可求得 AC=√2,BC=10,AB=4,DF=2V√2,EF=2V10,DE=8, 所以AC=BC=AB 1 DE EF D正=2》 所以△ABC∽△DEF. 【方法归纳】 证明方格中的三角形相似的常用方法: (1)利用勾股定理求出各边长; (2)求出三组对应边的比值; (3)比较三个比值,看是否相等若相等,则两个三角形相似
证明:由勾股定理,可求得 AC= 𝟐,BC= 𝟏𝟎,AB=4,DF=2 𝟐,EF=2 𝟏𝟎,DE=8, 所以𝐀𝐂 𝐃𝐅 = 𝐁𝐂 𝐄𝐅 = 𝐀𝐁 𝐃𝐄 = 𝟏 𝟐 , 所以△ABC∽△DEF. 【方法归纳】 证明方格中的三角形相似的常用方法: (1)利用勾股定理求出各边长; (2)求出三组对应边的比值; (3)比较三个比值,看是否相等.若相等,则两个三角形相似

新知训川练织固 1.如图,在大小为4X4的正方形网格中,是相似三角形的是 (C) ① ② ③ ④ A.①和② B.②和③ C.①和③ D.②和④ 合
新知训练巩固 1.如图,在大小为4×4的正方形网格中,是相似三角形的是 ( C ). A.①和② B.②和③ C.①和③ D.②和④

2.一个直角三角形的一条直角边长和斜边长分别为8cm和15 cm,另一个直角三角形的一条直角边长和斜边长分别是6cm 45 和空cm,这两个直角三角形一相似三角形.(填“是”或“不 是”) 合
2.一个直角三角形的一条直角边长和斜边长分别为8 cm和15 cm,另一个直角三角形的一条直角边长和斜边长分别是6 cm 和 cm,这两个直角三角形是 相似三角形.(填“是”或“不 是”) 𝟒𝟓 𝟒

3.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,求证: △ABC△EFD, D B C E 证明:点D,E,F分别是AB,BC,CA的中点, ·DE 1 DF 1 EF 1 Z'BC 2'AB 2 EF ..AC BC AB '.△ABC∽△EFD. 合
3.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,求证: △ABC∽△EFD. 证明:∵点 D,E,F 分别是 AB,BC,CA 的中点, ∴ 𝐃𝐄 𝐀𝐂 = 𝟏 𝟐 , 𝐃𝐅 𝐁𝐂 = 𝟏 𝟐 , 𝐄𝐅 𝐀𝐁 = 𝟏 𝟐 . ∴ 𝐃𝐄 𝐀𝐂 = 𝐃𝐅 𝐁𝐂 = 𝐄𝐅 𝐀𝐁 . ∴△ABC∽△EFD