
家庭猴伞 第1课时 用树状图或表格求简单事件发生的概率
第1课时 用树状图或表格求简单事件发生的概率

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.利用树状图或表格,我们可以不 不 地列出 所有可能的结果,从而比较方便地求某些事件发生的概率 2.某校高一年级今年计划招四个班的新生,并采取随机摇号 的方法分班,小明和小红既是该校的高一新生,又是好朋友,则 小明和小红分在同一个的机会是(A) A号 B 3 3.同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的 概率为(A). B D 3-4
基础自主梳理 1.利用树状图或表格,我们可以不重复 、不遗漏 地列出 所有可能的结果,从而比较方便地求某些事件发生的概率. 2.某校高一年级今年计划招四个班的新生,并采取随机摇号 的方法分班,小明和小红既是该校的高一新生,又是好朋友,则 小明和小红分在同一个的机会是( ). A. 𝟏 𝟒 B. 𝟏 𝟑 C. 𝟏 𝟐 D. 𝟑 𝟒 3.同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的 概率为( ). A. 𝟏 𝟒 B. 𝟏 𝟑 C. 𝟏 𝟐 D. 𝟑 𝟒 A A

核心重难探究 知识点一用树状图或表格求简单事件发生的概率 【例1】小红的衣柜里有2件上衣,1件是长袖,1件是短袖;3 条裙子,分别是黄色、红色、蓝色.她任意拿出1件上衣和1条 裙子,正好是短袖上衣和红色裙子的概率是多大? 思路点拨:先通过列表或画树状图得任意拿出1件上衣和1条 裙子的所有等可能结果,再利用概率公式计算正好是短袖上 衣和红色裙子的概率
核心重难探究 知识点一 用树状图或表格求简单事件发生的概率 【例1】小红的衣柜里有2件上衣,1件是长袖,1件是短袖;3 条裙子,分别是黄色、红色、蓝色.她任意拿出1件上衣和1条 裙子,正好是短袖上衣和红色裙子的概率是多大? 思路点拨:先通过列表或画树状图得任意拿出1件上衣和1条 裙子的所有等可能结果,再利用概率公式计算正好是短袖上 衣和红色裙子的概率
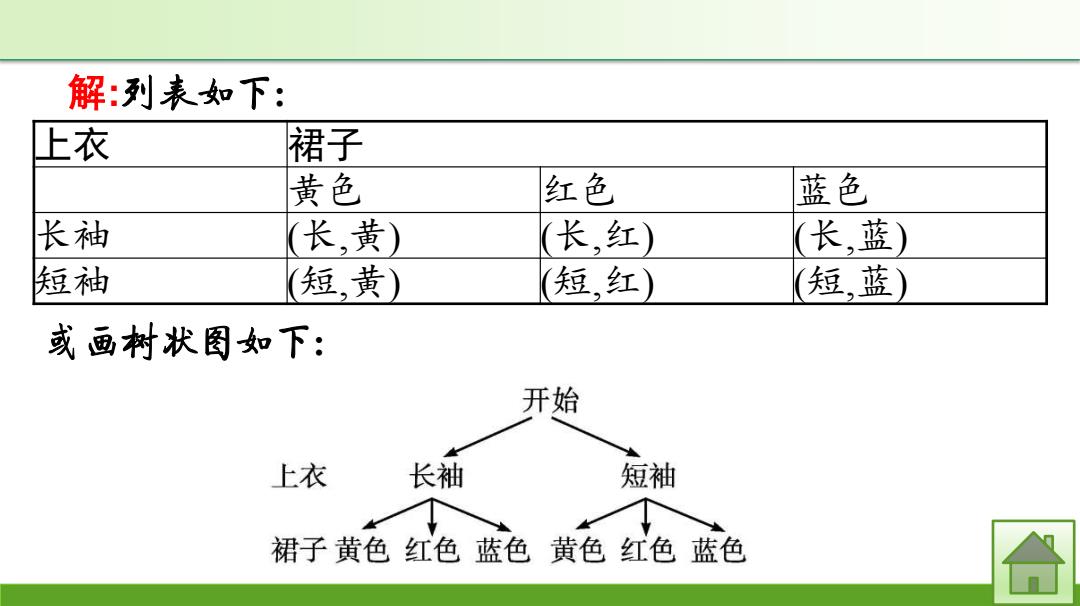
解:列表如下: 上衣 裙子 黄色 红色 蓝色 长袖 (长,黄) (长,红) (长,蓝) 短袖 (短,黄) (短,红) (短,蓝) 或画树状图如下: 开始 上衣 长袖 短袖 裙子黄色红色蓝色黄色红色蓝色 合
解 :列表如下: 上衣 裙子 黄色 红色 蓝色 长袖 ( 长 , 黄 ) ( 长 , 红 ) ( 长 , 蓝 ) 短袖 ( 短 , 黄 ) ( 短 , 红 ) ( 短 , 蓝 ) 或画树状图如下:

由表格或树状图可知,共有6种等可能结果,其中正好是短袖 上衣和红色裙子的结果只有1种,故其概幸是石 合
由表格或树状图可知,共有6种等可能结果,其中正好是短袖 上衣和红色裙子的结果只有1种,故其概率是 𝟏 𝟔

【方法归纳】 当一次试验要涉及两个因素(例如投掷两枚质地均匀的骰子) 或两次操作(如先后两次投掷一枚质地均匀的骰子),并且可能 出现的结果数较多时,为不重不漏地列出所有可能的结果,通 常采用列表法或画树状图法.用列表法求含两次操作或两个 因素的事件的概率时,先选其中的一次操作或一个因素作为 横行,另一次操作或另一因素作为竖列,列出表格,进而得到事 件发生的所有可能结果,再看我们关注的事件出现的次数与 总数的比值
【方法归纳】 当一次试验要涉及两个因素(例如投掷两枚质地均匀的骰子) 或两次操作(如先后两次投掷一枚质地均匀的骰子),并且可能 出现的结果数较多时,为不重不漏地列出所有可能的结果,通 常采用列表法或画树状图法.用列表法求含两次操作或两个 因素的事件的概率时,先选其中的一次操作或一个因素作为 横行,另一次操作或另一因素作为竖列,列出表格,进而得到事 件发生的所有可能结果,再看我们关注的事件出现的次数与 总数的比值

知识点二利用概率评判规则的合理性 【例2】某书店参加某校读书活动,并为每班准备了A,B两 套名著,赠予各班两名优秀读者,以资鼓励某班决定采用游戏 方式发放给甲、乙两名优秀读者,其规则如下:将三张除了数 字分别为2,5,6不同外其余均相同的扑克牌,数字朝下随机平 铺于桌面,从中任取2张若牌面数字之和为偶数,则甲获A名著; 若牌面数字之和为奇数,则乙获A名著.你认为此规则合理吗? 为什么? 思路点拨:画树状图或列表,获得牌面数字之和的所有结果 数,计算出甲与乙获A名著的概率,进而评判规则的合理性
知识点二 利用概率评判规则的合理性 【例2】某书店参加某校读书活动,并为每班准备了A,B两 套名著,赠予各班两名优秀读者,以资鼓励.某班决定采用游戏 方式发放给甲、乙两名优秀读者,其规则如下:将三张除了数 字分别为2,5,6不同外其余均相同的扑克牌,数字朝下随机平 铺于桌面,从中任取2张.若牌面数字之和为偶数,则甲获A名著; 若牌面数字之和为奇数,则乙获A名著.你认为此规则合理吗? 为什么? 思路点拨:画树状图或列表,获得牌面数字之和的所有结果 数,计算出甲与乙获A名著的概率,进而评判规则的合理性

解:此规则不合理.画树状图如下: 开始 第一张 第二张5 6 2 6 2 5 和 7 8 7 11 8 11 可知等可能的6种结果中,和为偶数的有2种,和为奇数的 内4种,所以P(甲茨A名著)名=P(乙茨A名著)君=子 所以乙获得A名著的概率大些,故此规则不合理
解:此规则不合理.画树状图如下: 可知等可能的 6 种结果中,和为偶数的有 2 种,和为奇数的 有 4 种,所以 P(甲获 A 名著)=𝟐 𝟔 = 𝟏 𝟑 ,P(乙获 A 名著)=𝟒 𝟔 = 𝟐 𝟑 . 所以乙获得 A 名著的概率大些,故此规则不合理

方法归纳】 判断一个规则是否合理或游戏是否公平,就看所涉及的事件 在同等条件下发生的概率是否相等若概率相等,则这个规则 合理或游戏公平,否则就不合理或不公平. 合
【方法归纳】 判断一个规则是否合理或游戏是否公平,就看所涉及的事件 在同等条件下发生的概率是否相等.若概率相等,则这个规则 合理或游戏公平,否则就不合理或不公平