
家庭馆亚 第2课时 矩形的判定
第2课时 矩形的判定

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.矩形的判定定理 1)对角线 的平行四边形是矩形 (2)有三个角是 的四边形是矩形
基础自主梳理 1.矩形的判定定理 (1)对角线相等 的平行四边形是矩形. (2)有三个角是直角 的四边形是矩形

温馨提示 与菱形类似,矩形的两个判定定理与它的两个性质定理分别 是互逆定理注意这两种判定方法的起点不同,即一种是基于 “平行四边形”的起点而开始判别的,一种是从“四边形”的基 础上进行判别的.明确了这些细节,便于我们对矩形判定定理 的理解、记忆与应用
温馨提示 与菱形类似,矩形的两个判定定理与它的两个性质定理分别 是互逆定理.注意这两种判定方法的起点不同,即一种是基于 “平行四边形”的起点而开始判别的,一种是从“四边形”的基 础上进行判别的.明确了这些细节,便于我们对矩形判定定理 的理解、记忆与应用

2.下面检查一个四边形门框是否为矩形的方法中正确的是 (D) A.用卷尺测量对角线是否互相平分 B.用卷尺测量对角线是否相等 C.用曲尺测量对角线是否互相垂直 D.用曲尺测量门框的三个角是否为直角 合
2.下面检查一个四边形门框是否为矩形的方法中正确的是 ( ). A.用卷尺测量对角线是否互相平分 B.用卷尺测量对角线是否相等 C.用曲尺测量对角线是否互相垂直 D.用曲尺测量门框的三个角是否为直角 D
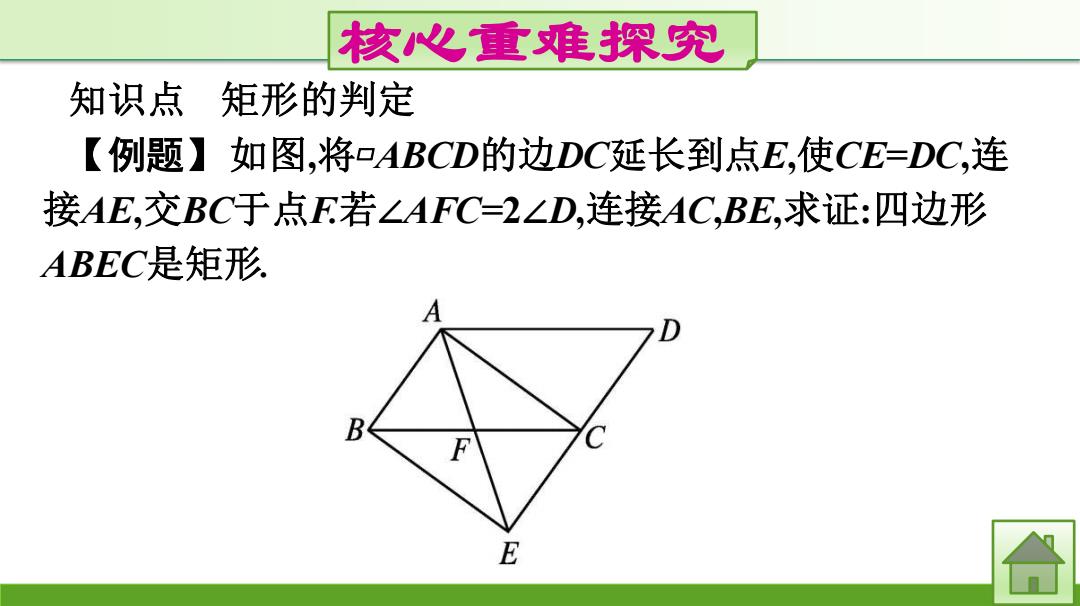
核心重难探究 知识点 矩形的判定 【例题】如图,将ABCD的边DC延长到点E,使CE=DC,连 接AE,交BC于点F若∠AFC=2∠D,连接AC,BE,求证:四边形 ABEC是矩形, B E 合
核心重难探究 知识点 矩形的判定 【例题】如图,将▱ABCD的边DC延长到点E,使CE=DC,连 接AE,交BC于点F.若∠AFC=2∠D,连接AC,BE,求证:四边形 ABEC是矩形

思路点拨:()四边形ABEC是什么特殊的四边形? (2)FB=FA吗?为什么?由此可用什么方法判定四边形ABEC 是矩形? (3)AE=AD吗?为什么?由此可用什么方法判定四边形ABEC 是矩形? 合
思路点拨:(1)四边形ABEC是什么特殊的四边形? (2)FB=FA吗?为什么?由此可用什么方法判定四边形ABEC 是矩形? (3)AE=AD吗?为什么?由此可用什么方法判定四边形ABEC 是矩形?

证明:(方法1)在口ABCD中,AB=CD,ABII CD. .CE=DC,.∴,AB=CE,ABCE. '.四边形ABEC是平行四边形. ∴AF=EF,BF=CF. 在ABCD中,∠D=∠ABC.又∠AFC=2∠D, .'.∠AFC=2∠ABC=∠ABC+∠BAE, .∴.∠ABC=∠BAE,∴,AF=BF,∴,AE=BC 故口ABEC是矩形. 合
证明:(方法1)在▱ABCD中,AB=CD,AB∥CD. ∵CE=DC,∴AB=CE,AB∥CE. ∴四边形ABEC是平行四边形. ∴AF=EF,BF=CF. 在▱ABCD中,∠D=∠ABC.又∠AFC=2∠D, ∴∠AFC=2∠ABC=∠ABC+∠BAE, ∴∠ABC=∠BAE,∴AF=BF,∴AE=BC. 故▱ABEC是矩形

(方法2)同方法1,可证四边形ABEC是平行四边形. 在口ABCD中,ADII BC,'.∠D=∠BCE. .∠AFC=2∠D, .∴.∠AFC=2∠BCE=∠BCE+∠AED, ∴∠BCE=∠AED,∴.∠D=∠AED,∴.AE=AD .CE=DC,∴.AC⊥DE,∠ACE=0°, ∴.口ABEC是矩形
(方法2)同方法1,可证四边形ABEC是平行四边形. 在▱ABCD中,AD∥BC,∴∠D=∠BCE. ∵∠AFC=2∠D, ∴∠AFC=2∠BCE=∠BCE+∠AED, ∴∠BCE=∠AED,∴∠D=∠AED,∴AE=AD. ∵CE=DC,∴AC⊥DE,∠ACE=90° , ∴▱ABEC是矩形

【方法归纳】 1.判定一个四边形是矩形,可先判定它是平行四边形,再证明 有一个角是直角或对角线相等,也可直接证明有三个角是直 角. 2.从四边形到平行四边形需添加两个独立条件,从平行四边 形到矩形需添加一个条件
【方法归纳】 1.判定一个四边形是矩形,可先判定它是平行四边形,再证明 有一个角是直角或对角线相等,也可直接证明有三个角是直 角. 2.从四边形到平行四边形需添加两个独立条件,从平行四边 形到矩形需添加一个条件