
家庭猴伞 第3课时 菱形的性质与判定的综合应用
第3课时 菱形的性质与判定的综合应用

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.菱形的面积=底X高=对角线乘积的一半进而可以推广得 到如下结论:对角线互相垂直的四边形的面积等于对角线乘 积的一半 2.如图,四边形ABCD的四条边相等,且面积为120cm2,对角 线AC=24cm,则四边形ABCD的周长为(A), B A.52 cm B.40 cm C.39 cm D.26 cm
基础自主梳理 1.菱形的面积=底×高=对角线乘积的一半.进而可以推广得 到如下结论:对角线互相垂直的四边形的面积等于对角线乘 积的一半. 2.如图,四边形ABCD的四条边相等,且面积为120 cm2 ,对角 线AC=24 cm,则四边形ABCD的周长为( ). A.52 cm B.40 cm C.39 cm D.26 cm A

3.已知一个菱形的边长为2,较长的对角线长为23,则这 个菱形的面积是
3.已知一个菱形的边长为 2,较长的对角线长为 2 𝟑,则这 个菱形的面积是 2 𝟑
核心重难探究 知识点 菱形的判定与性质的综合应用 【例题】如图,在四边形ABCD中,AB=AD,BD平分∠ABC, AC⊥BD,垂足为O A B (1)求证:四边形ABCD是菱形; (2)若CD=3,BD=2V5,求四边形ABCD的面积
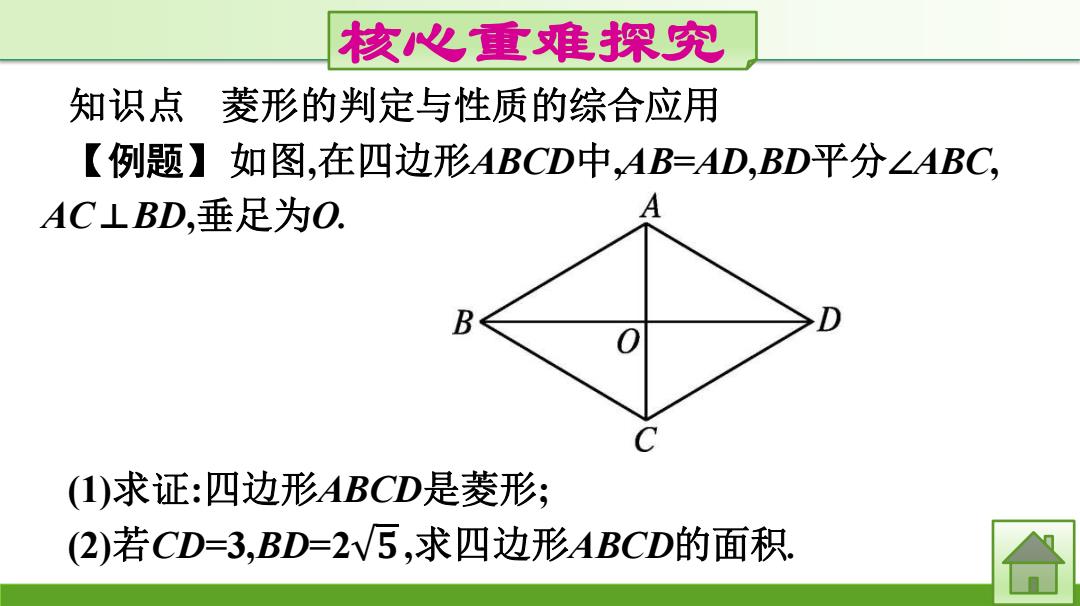
核心重难探究 知识点 菱形的判定与性质的综合应用 【例题】如图,在四边形ABCD中,AB=AD,BD平分∠ABC, AC⊥BD,垂足为O. (1)求证:四边形ABCD是菱形; (2)若CD=3,BD= 2 𝟓,求四边形ABCD的面积

思路点拨:(1)∠ABD,∠CBD及∠ADB相等吗?△AOD与 △COB是否全等?BC与AD有何关系?四边形ABCD是平行四 边形吗?其四条边是否相等?你有哪些方法证明四边形ABCD 是菱形? 由已知条件易证△AOD烂△COB,进而可通过对角线互相平 分且垂直证得结论; 2)如何求AC的长?菱形的面积与其对角线乘积的一半有何 数量关系?
思路点拨:(1)∠ABD,∠CBD及∠ADB相等吗?△AOD与 △COB是否全等?BC与AD有何关系?四边形ABCD是平行四 边形吗?其四条边是否相等?你有哪些方法证明四边形ABCD 是菱形? 由已知条件易证△AOD≌△COB,进而可通过对角线互相平 分且垂直证得结论; (2)如何求AC的长?菱形的面积与其对角线乘积的一半有何 数量关系?

(1)证明:.AB=AD,,∠ADB=∠ABD. .BD平分∠ABC,∴∠ABD=∠CBD, .'.∠ADB=∠CBD. .AC⊥BD,AB=AD,∴.BO=DO 在△AOD和△COB中, .∴∠AOD=∠COB,OB=OD,∠ADB=∠CBD, .∴.△AODg△COB.∴.AO=CO, '.四边形ABCD是平行四边形. 又AC⊥BD,'.口ABCD是菱形
(1)证明:∵AB=AD,∴∠ADB=∠ABD. ∵BD平分∠ABC,∴∠ABD=∠CBD, ∴∠ADB=∠CBD. ∵AC⊥BD,AB=AD,∴BO=DO. 在△AOD和△COB中, ∵∠AOD=∠COB,OB=OD,∠ADB=∠CBD, ∴△AOD≌△COB.∴AO=CO, ∴四边形ABCD是平行四边形. 又AC⊥BD,∴▱ABCD是菱形

2)解:四边形ABCD是菱形,OD2BD=V5 在Rt△CDO中, 0C=√CD2.0D2=√32-(W52-2, .AC=4. S xARCD-AC-BD-x4x2V5-4V5. 合
(2)解:∵四边形 ABCD 是菱形,∴OD=𝟏 𝟐 BD= 𝟓. 在 Rt△CDO 中, OC= 𝐂𝐃𝟐-𝐎𝐃𝟐 = 𝟑𝟐-( 𝟓) 𝟐 =2, ∴AC=4. ∴S 菱形 ABCD= 𝟏 𝟐 AC·BD=𝟏 𝟐 ×4×2 𝟓=4 𝟓

【方法归纳】 1菱形的判定与性质是解与角、线段相关问题的重要依据 与途径 2.由于菱形的四条边相等,两条对角线互相垂直平分,故菱形 的问题常与直角三角形或等腰三角形联系在一起,这样有关 菱形的证明与计算常转化到等腰三角形或直角三角形中去解 决.注意体会证明过程中所运用的数学思想方法:
【方法归纳】 1.菱形的判定与性质是解与角、线段相关问题的重要依据 与途径. 2.由于菱形的四条边相等,两条对角线互相垂直平分,故菱形 的问题常与直角三角形或等腰三角形联系在一起,这样有关 菱形的证明与计算常转化到等腰三角形或直角三角形中去解 决.注意体会证明过程中所运用的数学思想方法

新知训川练织固 1.如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标 为(1,2),则菱形OABC的面积是(B),. A.V5 B.2V5 C.2V3 D.2V5-1 A X 合
新知训练巩固 1.如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标 为(1,2),则菱形OABC的面积是( ). A. 𝟓 B.2 𝟓 C.2 𝟑 D.2 𝟓-1 B