
家庭馆亚 第l课时 矩形的性质
第1课时 矩形的性质

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.矩形的定义 有一个角是直角的 叫做矩形 2.矩形的性质定理 (1)矩形的四个角都是 (2)矩形的对角线 3.已知在矩形ABCD中,对角线AC,BD相交于点O,则与 ∠OAB相等的角有(不包括∠OAB)(O A.1个 B.2个C.3个D.4个 解析:∠OBA,∠ODC,∠OCD均与∠OAB相等,故选C
基础自主梳理 1.矩形的定义 有一个角是直角的平行四边形 叫做矩形. 2.矩形的性质定理 (1)矩形的四个角都是直角 . (2)矩形的对角线相等 . 3.已知在矩形ABCD中,对角线AC,BD相交于点O,则与 ∠OAB相等的角有(不包括∠OAB)( ). A.1个 B.2个 C.3个 D.4个 解析:∠OBA,∠ODC,∠OCD均与∠OAB相等,故选C. C

4.直角三角形的性质定理 直角三角形斜边上的中线等于 5.已知在△ABC中,AB=5cm,BC=12cm,AC=13cm,则AC边 上的中线BD的长为cm
4.直角三角形的性质定理 直角三角形斜边上的中线等于斜边的一半 . 5.已知在△ABC中,AB=5 cm,BC=12 cm,AC=13 cm,则AC边 上的中线BD的长为 cm. 𝟏𝟑 𝟐
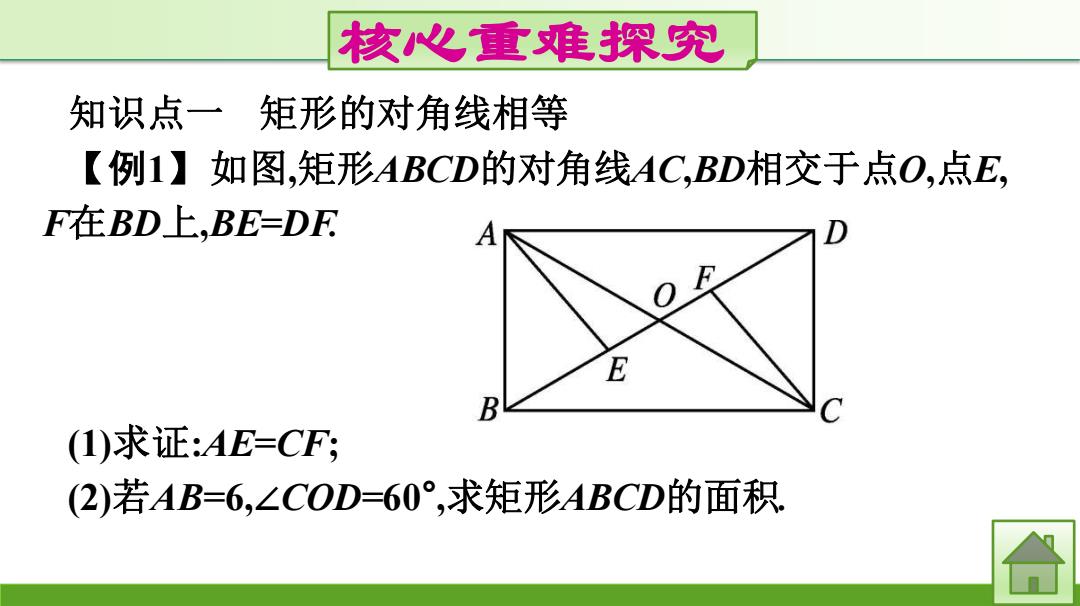
核心重难探究 知识点一 矩形的对角线相等 【例1】如图,矩形ABCD的对角线AC,BD相交于点O,点E, F在BD上,BE=DF B (1)求证:AE=CF; (2)若AB=6,∠COD=60°,求矩形ABCD的面积
核心重难探究 知识点一 矩形的对角线相等 【例1】如图,矩形ABCD的对角线AC,BD相交于点O,点E, F在BD上,BE=DF. (1)求证:AE=CF; (2)若AB=6,∠COD=60° ,求矩形ABCD的面积

思路点拨:(1)要证AE=CF,可以证明这两边所在的两个三角 形全等,即可证明△ABE烂△CDF,或者证明△AOE烂△COF; 也可以连接CE,AF,证明四边形AECF是平行四边形. (2)由条件易知△OCD为等边三角形,故∠ACD=60°,再求AD 的长,即可计算矩形ABCD的面积
思路点拨:(1)要证AE=CF,可以证明这两边所在的两个三角 形全等,即可证明△ABE≌△CDF,或者证明△AOE≌△COF; 也可以连接CE,AF,证明四边形AECF是平行四边形. (2)由条件易知△OCD为等边三角形,故∠ACD=60° ,再求AD 的长,即可计算矩形ABCD的面积

(1)证明:.四边形ABCD为矩形,∴AB=CD,ABII CD, .∴∠ABE=∠CDF.又BE=DF,∴△ABE≈△CDF.∴.AE=CF (2)解:在矩形ABCD中,OC=之AC,OD=2BD,且AC-BD, .∴.OC=0D. .∠COD=60°,∴.△COD为等边三角形, .∠ACD=60°,.∠CAD=30°. 在Rt△ACD中,CD=AB=6,∴.AC=12. 由勾股定理,得AD=6V3. '.矩形ABCD的面积为AB·AD=6×6v3=36V3. 合
(1)证明:∵四边形ABCD为矩形,∴AB=CD,AB∥CD, ∴∠ABE=∠CDF.又BE=DF,∴△ABE≌△CDF.∴AE=CF. (2)解:在矩形ABCD中, OC=𝟏 𝟐 AC,OD=𝟏 𝟐 BD,且 AC=BD, ∴OC=OD. ∵∠COD=60° ,∴△COD为等边三角形, ∴∠ACD=60° ,∴∠CAD=30° . 在Rt△ACD中,CD=AB=6,∴AC=12. 由勾股定理,得 AD=6 𝟑. ∴矩形 ABCD 的面积为 AB·AD=6×6 𝟑=36 𝟑

【方法归纳】 在解决矩形的问题时,要充分考虑它的性质,应用其性质把 矩形问题转化为等腰三角形或直角三角形的问题来解决
【方法归纳】 在解决矩形的问题时,要充分考虑它的性质,应用其性质把 矩形问题转化为等腰三角形或直角三角形的问题来解决
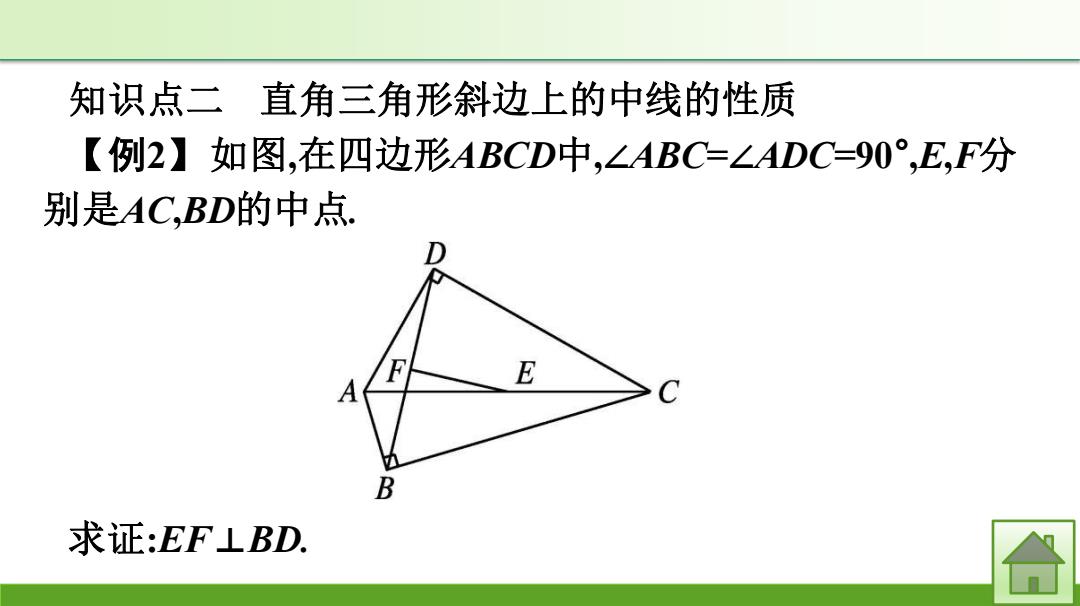
知识点二直角三角形斜边上的中线的性质 【例2】如图,在四边形ABCD中,∠ABC=∠ADC=90°,E,F分 别是AC,BD的中点. F A E B 求证:EF⊥BD
知识点二 直角三角形斜边上的中线的性质 【例2】如图,在四边形ABCD中,∠ABC=∠ADC=90° ,E,F分 别是AC,BD的中点. 求证:EF⊥BD

思路点拨:(1)结合已知条件与结论,EF与BD有何关系? (2)Rt△ACD与Rt△ACB有何特征? (3)联想线段垂直平分线或等腰三角形的特征,连接DE,BE, 它们相等吗?为什么? 证明:连接DE,BE,图略. .∵∠ABC=∠ADC=90°,且E是AC的中点, .'DE=BE.又DF=BF,.∴.EF⊥BD 合
思路点拨:(1)结合已知条件与结论,EF与BD有何关系? (2)Rt△ACD与Rt△ACB有何特征? (3)联想线段垂直平分线或等腰三角形的特征,连接DE,BE, 它们相等吗?为什么? 证明:连接DE,BE,图略. ∵∠ABC=∠ADC=90° ,且E是AC的中点, ∴DE=BE.又DF=BF,∴EF⊥BD